Inscription / Connexion Nouveau Sujet
Comparer des aires.
Bonjour, j'aimerais avoir de l'aide pour cet exercice, merci d'avance.
ABCD est un trapèze rectangle avec AD=CD= 4cm, AB= 8 cm.
Le point E est un point du segment [AD].
La parallèle à (AB) passant par E coupe [BC] en F.
A) Avec les formules algébriques
1. On note f(x) l'aire de ABFE (en cm²).
a. Soit G le point d'intersection des droites (AD) et (BC). Justifier que le triangle GEF est rectangle isocèle en E.
En déduire EF en fonction de x puis démontrer que f(x)= 1/2 x(16-x).
b. Calculer l'aire du trapèze ABCD en cm². Expliquer pourquoi chercher E tel que ABFE et EFCD aient la même aire revient à chercher x tel que f(x)=12.
c. A l'aide de la calculatrice, déterminer le nombre d'antécédents de 12 par f. Calculer f(8-2 10) et conclure.
10) et conclure.
Bonsoir,
1)
a)
Tu projettes C en H sur [AB] donc (CH)  (AB). OK ?
(AB). OK ?
AH=DC=4
HB=8-4=4
HC=AD=4
Le tri CHB est rectangle isocèle en H donc angle HBC=45°
Donc angle ABG=45°
et angle EFG=45° aussi ( angles correspondants pour les // (AB) et (EF).)
(FE)//(AB)
(AB)  (AG)
(AG)
donc (EG) (FE)
(FE)
Le tri GEF est rectangle en E avec angle EFG=45° donc angle EGF=90-45=45°.
Le tri GEF est isocèle car il a ses angles à la base égaux.
1)
a)suite :
Donc EF=EG
De même le tri CDG est rect. isocèle en D donc DG=DC=4
EF=EG=GD+DE=4+4-x=8-x
aire trapèze ABFE=(AB+EF)*AE/2=(8+8-x)*x/2=(1/2)x(16-x)
f(x)=(1/2)x(16-x)
b)
aire ABCD=(8+4)*4/2=24
Expliquer pourquoi chercher E tel que ABFE et EFCD aient la même aire revient à chercher x tel que f(x)=12.
Car aire ABFE+aire EFCD=24.
S'ils ont même aire, il faut que chacun ait pour aire : 24/2=12
c. A l'aide de la calculatrice, déterminer le nombre d'antécédents de 12 par f
f(x)=-x²/2+ 8x après développement.
Tu en trouves un seul : x
 1.7
1.7
f(8-2
 10)=-(8-2
10)=-(8-2 10)2/2 + 8(8-2
10)2/2 + 8(8-2 10)
10)
Tu développes et tu trouves 12 après qq. calculs pas très faciles!!!!
Merci beaucoup pour votre aide mais pourriez vous m'expliquer pourquoi dans le 1. a)(à la 2ème question),
EF=EG=GD+DE=4+4-x=8-x et non EF=EG=GD+DA=4+4-x=8-x ???
Et sinon pour la dernière question, d'ou vient le calcul
f(x)=-x²/2+ 8x après développement.
Et enfin pour le dernier calcul j'ai essayer :
f(8-2 10)
10)
= -(8-2 10)²/2 + 8(8-2
10)²/2 + 8(8-2 10)
10)
= -(64+4 10)/2 + (8*8 + 8*(-2) + 8
10)/2 + (8*8 + 8*(-2) + 8 10)
10)
= -(64+4 10)/2 + (64-16+8
10)/2 + (64-16+8 10)
10)
= - (32 + 2 10) + (48+8
10) + (48+8 10)
10)
= - 32 - 2 10) + 48 + 8
10) + 48 + 8 10
10
= 16 - 6 10
10
 -2.97
-2.97
Je sais que ce n'est pas bon mais pouvez vous me dire mes erreurs ?!
Merci d'avance 
Oups je viens de voir mon erreur !
f(8-2 10)
10)
= -(8-2 10)²/2 + 8(8-2
10)²/2 + 8(8-2 10)
10)
= -(64+4*10)/2 + 8*8 - 8*2 10
10
= - 32 + 2 10 + 64-16
10 + 64-16 10
10
= - 32+2 10 + 64-16
10 + 64-16 10
10
= 32 - 14 10
10
 0.38
0.38
Je n'y arrive pas 
Alors on y va :
f(x)=-x2/2 + 8x
f(8-2 10)=-[(8-2
10)=-[(8-2 10)2]/2+8(8-2
10)2]/2+8(8-2 10)
10)
...=-[64-2*8*2 10+(2
10+(2 10)2]/2 +64-16
10)2]/2 +64-16 10
10
Tu sais que (2 10)2)=4*10=40
10)2)=4*10=40
f(8-2 10)=-(64-32
10)=-(64-32 10+40)/2 + 64-16
10+40)/2 + 64-16 10
10
....=-(104-32 10)/2 + 64-16
10)/2 + 64-16 10
10
...= -104/2 +(32 10)/2+64-16
10)/2+64-16 10
10
...=-52 + 16 10 +64 - 16
10 +64 - 16 10
10
...=-52+64
...=12
Avec les (....) précédées du signe moins, les racines , les carrés, la division de x2 par 2 , il n'est pas évident de ne pas faire d'erreurs !! Et difficile à taper.
Refais tranquillement au brouillon. OK?
En fait, je n'avais pas regardé ce que tu as fait et je le fais maintenant.
Tu as oublié le double produit en développant :
-(8-2 10)2
10)2
-(a-b)2=-(a2-2ab+b2)
Le "-2ab" n'est pas là !!
Donc j'ai juste a remplacer les points devant le égal par f(8-2
 10)???
10)???Oui, c'est ça : je voulais m'éviter des "copier-coller" à n'en plus finir !!
Dernière question !
Pour :
f(x)=-x²/2+ 8x après développement.
Tu en trouves un seul : x 1.7
1.7
C'est un moi de calculer -x²/2 + 8x ?
L'énoncé dit :
c. A l'aide de la calculatrice, déterminer le nombre d'antécédents de 12 par f.
Je ne sais pas comment tu t'y prends avec ta calculatrice en 2nde.
Tu dois savoir y entrer une fct ?
Donc tu entres : f(x)=-x²/2 + 8x
ou plutôt y=-x²/2+8x
que tu peux écrire :
y=(-1/2)*x²+8*x ou y=-0.5*x²+8*x
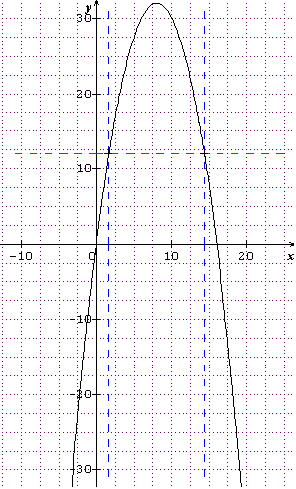
Tu peux faire afficher le graph et tu vois que tu as 2 antécédents de 12 par f et non 1 seul comme j'ai écrit ( car le 2ème n'est pas sur [0;4])
Donc tu vas écrire que 12 a 2 antécédents par f. J'ai tracé la droite y =12 en pointillés rouges et je redescends en bleu (pointillés) vers l'axe des x.
Sur mon graph :
axe des x et des y : 1 cm=2.5 unités . Attention !!
Je t'envoie une autre technique ensuite :
L'autre technique :
Tu entres ta fct dans la calculatrice avec :
départ : 0
pas : 1 ( qui veut dire que x part de 0 et augmente de 1 en 1)
Et tu fais défiler les valeurs :
x...y
0... 0
1... 7,5
2... 14
3... 19,5
4... 24
5... 27,5
6... 30
7... 31,5
8... 32
9... 31,5
10... 30
11... 27,5
12... 24
13.... 19,5
14...14
15... 7,5
Tu vois que y ( c'est-à-dire f(x)) passe par la valeur 12 pour :
1 < x1 < 2
et
14 < x2 < 15
12 a donc 2 antécédents par f dont un seul sur [0;4].
Je ne vois pas ce que tu peux faire d'autre en 2nde. Franchement, je ne vois pas. Le mieux , à ce niveau, semble être le graph.
A toi de voir.


