Inscription / Connexion Nouveau Sujet
DM 5ème Quadrilatère avec Geogebra
Bonsoir,
J'ai un autre exercice pour mon devoir maison que je ne comprends pas. Voici l'énoncé :
1) a. Tracer un quadrilatère DRIL et tracer ses diagonales. Nommer A le point d'intersection de ses diagonales.
b. Tracer la droite (d) parallèle à (LR) passant par I, puis la droite (e) parallèle à (LR) passant par D. Tracer la droite (f) parallèle à (IDà passant par L, puis la droite (g) parallèle à (ID) passant par R. Nommer B,C,E et F les point d'intersection de ces droites comme ci dessous.
Jusque là tout va bien.
2. a. Quelle semble être la nature du quadrilatère BCEF ?
b. Le démontrer. Ma réponse : Le quadrilatère BCEF est un parallélogramme car [BE] et [CF] ont le même milieu. Les droites (d) et (e) sont parallèles. Les droites (f) et (g) sont parallèles.
A partir de là, j'ai pas compris.. =s
3. a. En déformant le quadrilatère DRIL, conjecturer dans quels cas BCEF est un rectangle.
b. Le démontrer.
4. a. Dans quels cas BCEF est-il un losange ? Expliquer pourquoi.
b. Déduire des questions précédentes les conditions que doit vérifier DRIL pour que BCEF soit un carré.
Pouvez-vous m'aider s'il vous plaît ?
Voici le schéma de ce que j'ai déjà fait :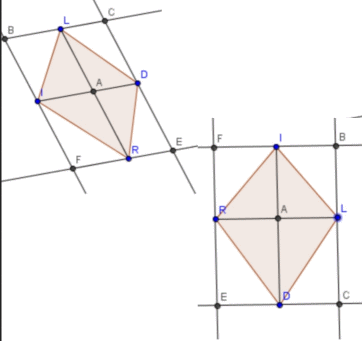
* Océane > image placée sur le serveur de l' , merci d'en faire autant la prochaine fois Lilas25
, merci d'en faire autant la prochaine fois Lilas25  *
*
Bonsoir !
J'ai une petite question avant de t'aider ;
Quand on dit tracer un quadrilatère, tu as tracé un quadrilatère quelconque ou un parallélogramme ?
Car même si les parallélogrammes sont des quadrilatères particuliers, ne commence jamais avec les cas particuliers !
Méfie toi des dessins fournit avec un énoncé, ils peuvent coller parfaitement comme il peuvent ne pas coller ;
Si on te dit "quadrilatère" préfère un quadrilatère quelconque ! Si tu fais un quadrilatère particulier tu auras toujours une possibilité pour que ce que tu démontre ne soit vraie que parce c'est un quadrilatère particulier ;
Par exemple : Sur tes dessin les diagonales (BE) et (CF) ont l'air de passer par A, or, sur mon dessin, DRIL est quelconque ! et on vient que les diagonales ne passent pas du tout par A...
De plus, si tu dis qu'elles se coupent en leur milieux tu dois dire pourquoi ! et non pas parce qu'on dirait !
Le quadrilatère FBCE est un parallélogramme car c'est côtés opposés sont parallèles !
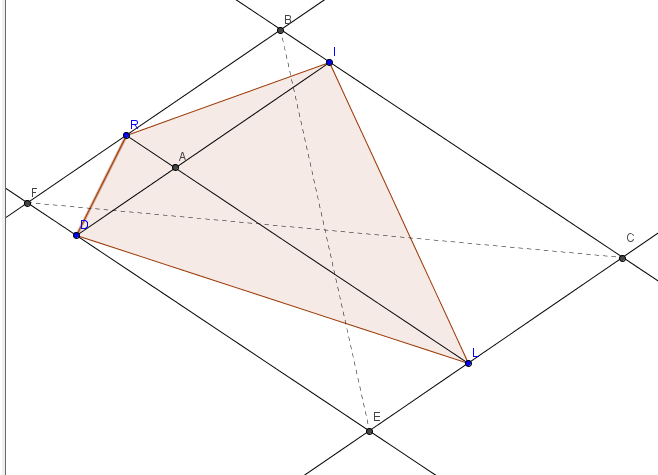
Passons à la suite ;
3. a. En déformant le quadrilatère DRIL, conjecturer dans quels cas BCEF est un rectangle.
b. Le démontrer.
Avec géogébra sait tu comment on fait pour déformer DRIL ou tu veux de l'aide ?
(Comme on doit le déformer, vouloir faire un dessin comme celui de l'énoncé ne servait à rien !)
3A. tu fais ça à l'oeil !
3B. tu pars de ce que tu as, à savoir BCFE est un rectangle, pour obtenir des conditions sur le quadrilatère DRIL et ça devrait passer tout seul !
4. a. Dans quels cas BCEF est-il un losange ? Expliquer pourquoi.
b. Déduire des questions précédentes les conditions que doit vérifier DRIL pour que BCEF soit un carré.
4A. Meme chose que pour le 3A, suppose que BCFE est un losange est énonces des conditions sur DRIL
4B. Un carré est un losange et un rectangle donc.... faut répondre aux questions avant 
Bonjour
Pour déformer clic droit sur un point et en maintenant appuyé glisser le point
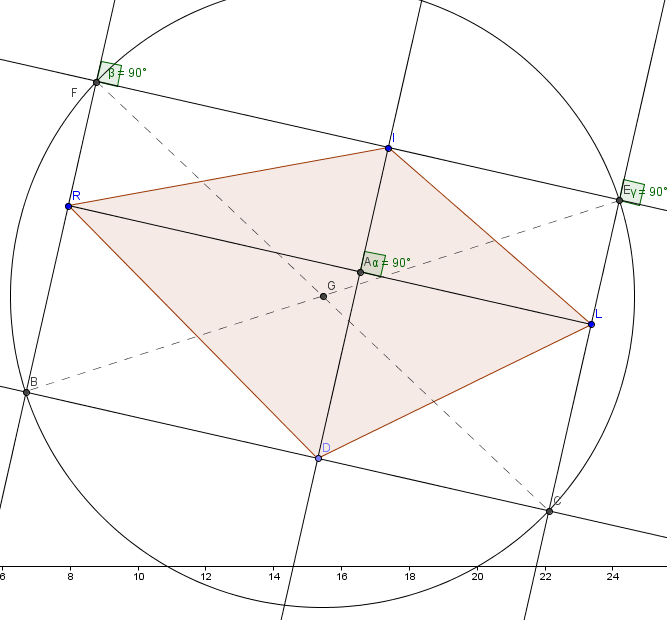
Figure déformée pour obtenir le carré BCEF
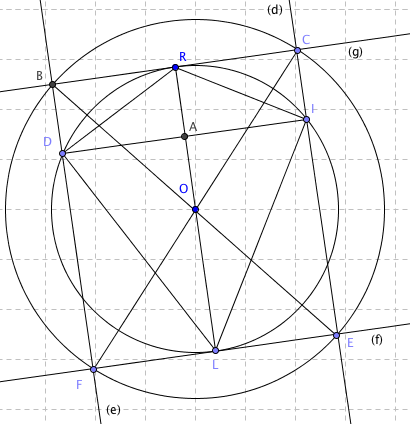
Bonsoir,
Avec ta souris , tu clique sur le premier icône, qui est un curseur, puis tu clique sur un point sans relâcher le clic de la souris, tu déplace ton point et tu relâche.
Attention ! Quand tu bouge un point de DRIL, supposons que tu déplace D, les points R, I et L ne doivent pas bouger !! C'est pour cela que quand tu forme ton quadrilatère DRIL sur géogébra, tu place quatre points au hasard sur l'écran, puis tu les relis avec ta fonction polygone, plutôt que crée un parallélogramme.
(Moi aussi je sais faire des beaux dessins 
Maintenant il faut trouver les conditions sur DRIL pour que BCEF soit un rectangle ;
Partons de la définition du rectangle :
- Ses côtés opposés sont parallèles et de même longueur
- Il a quatre anges droits
- Ses diagonales sont de même longueur et se coupent en leur milieux
Maintenant réfléchissons ;
- A t'il ses côtés opposés parallèles et de même longueur ?
==> Par construction on a en effet que ses cotés opposés sont parallèles et de même longueur, et ceci peu importe comment est DRIL.
- A t'il 4 angles droits ? Visiblement si DRIL est quelconque on ne l'a pas;
==> Il nous faut donc une condition sur DRIL........
SOL : Pour que BCEF ait 4 angles droits, il faut que (BF) soit perpendiculaire à (FE) et cette condition est suffisante car (FE) et (BC) sont parallèles, donc toute droite perpendiculaire a l'une sera perpendiculaire à l'autre ! Et comme on a en plus que (BF) et (CE) sont parallèles, on aura bien 4 angles droit. Donc la question est "quelle condition sur DRIL me permettrais d'avoir (BF) soit perpendiculaire à (FE) ? "
Et la réponse est simplement que, étant donné la construction de BCEF, il faut et il suffit que (ID) et (RL) soient perpendiculaire.
- Ses diagonales sont elles de même longueur et se coupent elles en leur milieux ?
==> Maintenant qu'on a nos 4 angles droits, les triangles BFC et FEC sont égaux, tout comme FEB et BEC. Donc en appliquant Pythagore, on obtient bien que les diagonales sont de même longueur et se coupent en leur milieux.
On a donc qu'une seule condition sur DRIl pour que BCEF soit un rectangle.
4. a. Dans quels cas BCEF est-il un losange ? Expliquer pourquoi.
b. Déduire des questions précédentes les conditions que doit vérifier DRIL pour que BCEF soit un carré.
A. On procède de même ;
Propriétés du losange :
- Ses côtés opposés sont parallèles
- Ses côtés sont égaux deux à deux
- Ses diagonales se coupent en leur milieux et font un angle droit.
Réfléchissons ;
- Ses côtés opposés sont'il parallèles ?
==> Par construction, oui il le sont;
- Ses côtes sont il égaux deux à deux ? Si DRIL est quelconque on voit bien que non.
==> Il nous faut une condition sr DRIL....
SOL : On a part construction que [BF] = [DI], de même manière on a que [BC] = [RL]. Si on veut que [BC] = [BF], par les égalités qu'on vient d'écrire, il faut que [RL] = [DI]. Donc il suffit que les diagonales de DRIL soit égales pour que BCEF ait ses quatre côtés égaux.
- Ses diagonales se coupent elles en leur milieux et font elles un angle droit ?
==> Maintenant qu'on a les 4 côtés égaux, on sait que les triangles BCF et CFE sont identiques. On a donc [BG]=[EG], et G est donc bien le milieux de [BE]. De même pour les triangles BCE et BFE. Les diagonales se coupent bien en leur mileux.
==> Et l'angle droit ? (Sur mon dessin j'ai noté l'angle BCG = Beta et l'angle FBC = alp
et l'angle FBC = alp )
)
* Le triangle BCF est maintenant isocèle, donc l'angle BCF = l'angle BFC = 
Dans un triangle, la somme des angles fait 180, appliquons cette propriété au triangle BFC :
 +2
+2 =180 soit
=180 soit  = 90 -(
= 90 -( /2)
/2)
* Interessons nous maintenant au triangle BCG
Soit x = l'angle CGB; on veut montrer que x = 90.
On sait que (BE)est une bissectrice de l'angle FBC (G étant le milieux de [CF], le triangle BCE et le symétrique par l'axe (BE) du triangle BFE, donc (BE) coupe l'angle en deux angles égaux), on a donc que l'angle CBG =  /2
/2
Par la propriété précédente, on a que langle BCG + angle CGB + angle CBG = 180
Soit :  + x + (
+ x + ( /2) = 180 ; avec
/2) = 180 ; avec  = 90 -(
= 90 -( /2) on ontient :
/2) on ontient :
90 -( /2) + x + (
/2) + x + ( /2) = 180
/2) = 180
x = 180 - 90
= 90
Et on a bien un angle droit.
On a donc qu'une seule condition sur DRIl pour que BCEF soit un losange.
B. Pour que BCEF soit un carré, il faut qu'il soit un rectangle ET un losange ; par conséquent il faut que DRIL ait ses diagonales qui se coupent à angle droit et qu'elles soient de même longueur.

Bonsoir,
Merci beaucoup pour votre aide !
Pour la question 3) a. j'ai mis :
BCEF est un rectangle lorsque les segments [RL] et [ID] sont perpendiculaires.
Mais je ne sais pas trop comment le démontrer.. :$
Et pour le losange j'ai pas compris.. :s
Je crois que j'ai trouvé pour le losange, mais je ne suis pas sûre :
BCEF est un losange lorsque ses diagonales forment un angle droit.
Est-ce que c'est bon ?
Sinon, je ne sais toujours pas comment démontrer, je n'ai pas trop compris les calculs... :S
Bonsoir,
Je vais commencer par, relis ce que je t'ai mis !
Tu n'as pas l'air d'avoir lu car je t'ai mis les réponses que tu attend pour ton DM ainsi que les preuves.
Si ce n'est pas clair, je peux t'expliquer comment j'ai procédé ;
J'ai construis DRIL quelconque, et j'ai regardé comment était BCEF, en me basant sur ce qu'on voulait.
Dans le cas du rectangle; j'ai listé les propriétés du rectangle. Propriétés qu'on veut sur BCEF? car on veut que ce soit un rectangle.
Après avoir listé ses propriétés, j'ai regardé quelles propriétés on avait déjà, et quelle propriété il nous manquait pour que ce soit bien un rectangle.
J'ai constaté que la première propriété que j'ai listé est déjà vérifiée, je suis donc passons à la seconde.
La seconde propriété que j'ai listé, elle, n'est pas vérifier car BCEF n'a pas quatre angles droits. Donc on doit trouver comment faire pour qu'ils les aient.
Ensuite on vérifie que la dernière propriété du rectangle que j'ai listé est vérifié.
Et on fait de même pour le losange ;
Inspire toi de ce que j'ai fais ! toute les démonstrations sont là.
J'ai tout relu encore une fois...
Alors, BCEF est un rectangle lorsqu'il a 4 angles droits, ses côtés opposés sont parallèles et de même longueur
et ses diagonales sont de même longueur et se coupent en leur milieu ?
Et pour démontrer :
Comme il a 4 angles droits, les triangles BFC et FEC sont égaux, et les triangles FEB et BEC aussi ?
Alors, BCEF est un rectangle lorsqu'il a 4 angles droits, ses côtés opposés sont parallèles et de même longueur
et ses diagonales sont de même longueur et se coupent en leur milieu ?
Oui!
On sait que BCFE a ses côtés opposés parallèles et de même longueur car on l'a construit comme ça. Donc ce point là ne pose pas de problème.
Pour que BCFE ait 4 angles droits, il faut que les diagonales de DRIL soit perpendiculaire entre elles.
Une fois qu'il a ses quatre angles droit, on a une symétrie axiale (avec les diagonales du rectangle) et donc c'est à cause de ça que G est bien le milieux des diagonales de BCFE.
Donc, en conclusion, pour répondre à la question, Pour que BCFE soit un rectangle, il faut que les diagonales de DRIL se coupent à angle droit.
Alors pour le losange :
4) a. Dans quels cas BCEF est-il un losange ? Expliquer pourquoi.
Ma réponse : Pour que BCEF soit un losange, il faut que les diagonales de DRIL soit égales ; BCEF aura alors quatre côtés égaux.
b. Déduire des questions précédentes les conditions que doit vérifier DRIL pour que BCEF soit un carré.
Ma réponse : Pour que BCEF soit un carré, il faut qu'il soit un rectangle et un losange ; donc il faut que DRIL ait ses diagonales qui se coupent à angle droit et qu'elles soient de même longueur.
Est-ce que c'est bon ?
Mon devoir est à rendre demain.