Inscription / Connexion Nouveau Sujet
Démontrer une conjecture
Bonjour,
Je bloque à une question d'un exo...
Voici l'énoncé
Dans un repère orthonormé (O;I,J),A est le point de coordonnées (0;-1), M est un point ,distinct de O, qui décrit l'axe du point M.
On note "x" l'abscisse du point M.
La parallèle à la droite (AM) passant par I coupe l'axe des ordonnées en N.
H est le point tel que OMHN est un rectangle.
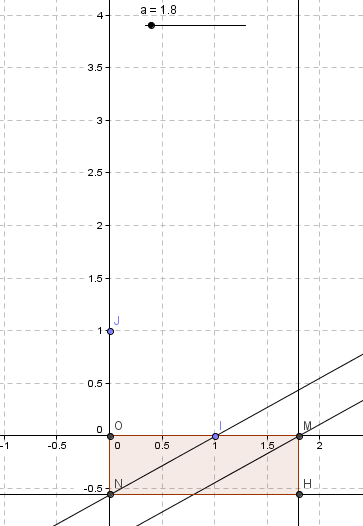
1/a. Avec un logiciel de géométrie dynamique , réaliser la figure.
Je l'ai faite voir ci-dessous.
b. Visualiser le lieu du point H lorsque M décrit l'axe des abscisses. Ça c'est bon
c. Emettre une conjecture sur la nature de ce lieu . J'ai mis que H décrit un ensemble de pts et que cet ensemble est une courbe d'équation y = -1/x
2/ Démontrer cette conjecture
Et là j'vois pas trop comment...
Merci d'avance ^^
Tu appliques Thalès aux triangles OIN et OMA qui sont semblables :
OI/ON = OM/OA
I: (1;0) A: (0;-1)
M: (x;0) N: (0;y)
H: (x;y)
OI/ON = OM/OA  1/y = x/(-1)
1/y = x/(-1)  y = -1/x
y = -1/x
Bonjour et merci pour votre aide...Seulement je ne comprends pas, les rapports ne sont pas :
OM/OI=OA/ON=MA/IN ?
Ahhhhhhhh, oui donc vous avez fait le produit en croix, n'est-ce pas ?
Mais là par contre oui je retrouve 1/y=x/-1 . M
Et là on inverse les trucs et puis c'est tout ? Comment l'expliquer à la rédaction ? :S
Comment l'expliquer à la rédaction ?
Comme ceci :
Les triangles OIN et OMA sont semblables (car IN // MA).
Donc d'après Thalès : OI/ON = OM/OA
 1/y = x/(-1)
1/y = x/(-1)
 y = -1/x
y = -1/xJe ne sais pas qu'en penses-tu ?
Est-ce que tu comprends l'explication ?
Est-ce que tu penses que si tu la comprends, ton prof la comprendras ?
Si la réponse est deux fois OUI, alors j'imagine qu'on peut dire que "ça suffit"...
Qu'est-ce qui te bloque ?
L'explication géométrique ?
Ou le calcul ?
Oups, j'voulais dire...
Genre en phrase de conclusion je met "On retrouve donc ce rapport, la conjecture est démontrée" ?
D'après Thalès :
OI/ON = OM/OA parce que IN et MA sont parallèles.
Comme rédaction ça suffit.
Après si tu ne connais pas, ou ne comprends, ou ne sait pas appliquer Thalès... c'est un autre problème  .
.
Genre en phrase de conclusion je met "On retrouve donc ce rapport, la conjecture est démontrée" ?
OI/ON = OM/OA
 1/y = x/(-1)
1/y = x/(-1)  y = -1/x
y = -1/x
Ce qui prouve la conjecture.
Mais si tu préfères mettre un poème pour dire la même chose, tu peux
 .
.
Affaire de goût.
Ok ok ^^''
Merci pour votre aide (je voudrais bien faire un poème pour vous remercier mais vous avez l'air de ne pas aimer  )
)
C'est juste que j'pensais qu'il fallait rajouter autre chose mais, trouver le rapport a l'air de suffir
je voudrais bien faire un poème pour vous remercier mais vous avez l'air de ne pas aimer
Essaie toujours
 .
.
Dans ce poème je vous remercierai
De la manière la plus sincère j'essaierai (Yoda est avec moi)
Votre aide m'a permis
De finir mon exercice, mon esprit, étant indécis
Et c'est pour cela que je vous remercie
Sur l'intervalle ]0; + l'infini[.
Voilà, c'est pas du V.Hugo mais bon xD
À la prochaine et merci encore ^^
A ce poème bien écrit
Je me régale d'un air ravi
Est-ce son sel que j'apprécie
Ou plus encore son esprit ?
Que son auteur le sache aussi
C'est lui même qu'il anoblit
Car l'avenir toujours sourit
A qui sait si bien dire merci



