Soit := { (x,y,z) ³ | x > 0 >, y > 0 , z > 0 , x + y > 2 ,  y + z > 2 , z + x > 2  }
Pour (x,y,z) ³ on pose g(x,y,z) = x² + y² + z² - 3 et , si pour (x,y,z) on a (x + y - z)(y + z - x)(z + x - y) 0 ( ce qu'il te faut prouver ) , on posera f(x,y,z) = x/(y + z - x)² +  y/(z + x - y)² + z/(x + y - z)² - 3/x²y²z²  .

.f et g sont C et
  .pour tout (x,y,z) de ³ Grad(g)(x,y,z) = 2(x,y,z)
  .pour tout (x,y,z) de Grad(f)(x,y,z) = (A(x,y,z) + 6/x³y²z² , A(x,y,z) + 6/y³z²x² , A(x,y,z) + 6/z³²x²y²) où A(x,y,z) = ....

  
Soit (u,v,w)) un point de où f  présente un extrêmum (u,v,w))  .  Grad(f)(u,v,w)) et Grad(g)(u,v,w)) ne sont donc pas linéairement indépendants et il existe un réel t tel que Grad(f)(u,v,w)) = t.Grad(g)(u,v,w))
Si on suppose qu'on a : 0 < u v w ( montre pourquoi on peut le supposer )prouve qu'on a alors  0 < u = v < w  ou  0 < u < v = w

A toi pour la suite...

Une correction : On n'a pas u < v < w don 3 cas sont possibles : u = v = w , u = v < w , u < v = w

Bonsoir,


Je remarque que :

En passant aux carrés correspond à


Avec a,b,c > 0 cette relation n'ajoute rien à



Egalité pour a=b=c=1 ,


Alain

Je me suis lamentablement trompé dans mes calculs .
Laisse donc tomber ce que j'ai écrit .
Il faut quand même montrer que (x + y - z)(y + z - x)(z + x - y) est non nul si (x,y,z)   0

En réponse à Alainpaul on peut remarquer que chaque dénominateur est strictement positif : a+b-c > 0 et les deux autres aussi

Et donc par la même occasion je réponds à ta question kybjm, étant donné que chaque terme est strictement positif

C'est comment tu montres que  x + y - z > 0 , y + z - x > 0 et z + x - y > 0 qui m'intéresse .

Je pense que ma démonstration est bonne, cependant je vois pas en quoi prouver tout ça m'aidera pour la solution finale...

x+y > 2 => x²+y² > 1

On peut en déduire donc que z² < 2 ( Car x² + y² + z² = 3 ) ( => z < 2 ) et donc que x+y-z > 0

Bonjour,
il me semble que la fonction où s=a+b+c est convexe donc on a par l'inégalité de Jensen
. Il reste à exploiter les contraintes pour terminer...

Bonsoir,


J'ai pensé à cette piste mais je ne suis pas arrivé
à une solution concrète,



Alain

Oui, moi non plus. J'ai pensé aux fonctions symétriques élémentaires mais ça n'a rien donné non plus.

Si on pose on est ramené à montrer que par ce qui précède... mais je ne suis même pas convaincu de ce qui précède (l'inégalité de Jensen est vraie sur un intervalle et là on a un trou quand même).

On sait en revanche que mais sans plus...

Bonjour,
il reste... donc à démontrer  

Bonsoir,


La présente égalité me remaine:




Alain

Bonjour,



Quelqu'un pourrait-il résumer la solution à laquelle
on aboutit ainsi que les différentes étapes parcourues,



merci,



Alain

bonjour,
@Alexique: Justement ton inégalité de 17h38 conduit à cette inégalité.

Or il y a un problème:

je demande à Yepa s'il ne se serait pas trompé dans le sens de son égalité.

Une évidence: Le domaine du triplet M(a,b,c) en tenant compte des contraintes est une calotte de la sphère x²+y²+z²=3 limitée par le demi-espace
En posant comme tu l'as fais judicieusement x+y+z=S ,( j'avais aussi introduis cette transformation en en m'interessant à l'interprétation géométrique des contraintes); on considère S comme paramètre appartenant à .

Pour S fixé le point (a,b,c) appartient à un cercle du plan x+y+z=s d'axe
, avec

Sur ce cercle je conjecture que le maximum de V(M)=xyz  est obtenu en  3 points :
I(a,a,c),avec c>a; J(a,b,b)avec a>b et K(a,b,a)avec b>a.  


Pour ces points on a V=uv² avec u²+2v²=3 et u+2v=S
En écrivant on parvient à :

Si alors

Après calculs simples j'aboutis à

L'inégalité pour revient à montrer que la moyenne de l'inverse de trois nombres positifs est supérieure ou égale à l'inverse de la moyenne, ce qui est clair par convexité de la fonction inverse.

Bon, en prenant a=1,1 b=1,2 et mon inégalité de Jensen n'est pas assez efficace pour démontrer ce qu'on veut (minoration trop grossière...).

Bonjour,
@GaBuZoMeu oui mon domaine est lacunaire, il me manque une pyramide de sommet

;
et donc il me faut allonger le domaine de S pour les plans X+Y+Z=S, et dans cette partie du domaine l'intersection avec la sphère n'est pas aussi simple.

@alainpaul
Comment passes-tu de à ta relation que reprend GABuZoMeu  à savoir (a+b)(b+c)(c+a)>8abc ?

De toute façon est fausse
Il suffit de la tester sur en fait un point très proche à cause de l'inégalité stricte des hypothèses;
et

Je que je viens d'écrire est stupide Ce point n'est pas sur la sphère.

@DOMOREA : je ne comprends rien à ce que tu écris sur le domaine.

Bonjour,

L'inégalité que je rappelais s'établit facilement:

en prenant les carrés,

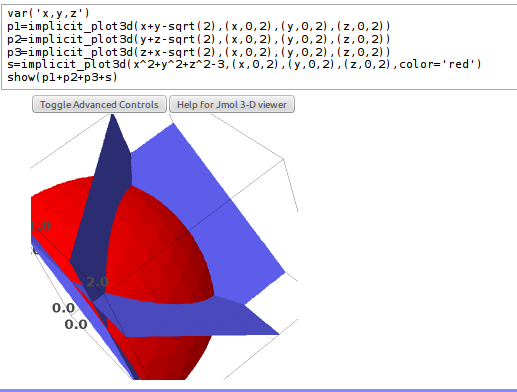
Le graphique couleur 3d est parlant,
recherche en cours,


Alain

Bonjour,
Une précision pour GaBuZoMeu
Voilà une image de piètre qualité qui représente le domaine en question
Le domaine sans la contrainte de la sphère
Au delà du plan ABC la sphère coupe un plan parallèle à ABC selon un cercle si ce plan ne dépasse pas le plan limite  parallèle à (ABC) et passant par S(1,1,1)

Dans un post précédent je considérais les plans parallèles variant entre ABC et le plan tangent à la sphère en S et j'avais oublié dans mon domaine le tétraèdre EABC

Un grand mea culpa : Ce que j'ai écris sur le sens de l'inégalité est faux ( confusion entre les deux parties de l'inégalité)

Maintenant revenons en aux différentes contributions
Je retiens celle d'alexique sur la convexité
puis alainpaul qui écrit (a+b)(b+c)(C+a)>8abc
et la phase finale toujours sur la convexité de 1/x donnée par GaBuZoMeu
Mais je n'ai pas vu où intervenaient les contraintes. Car les deux interventions utilisant   la notion de convexité  n'utilisent pas les contraintes.
La faiblesse il me semble dans le déficit d'explicatione d'alainpaul

J'avoue que je n'ai pas compris  pourquoi (a+b)(b+c)(C+a)>8abc
a-t-il déduis cela de S/3>(abc)² ?
J'aimerais avoir une réponse et savoir comment interviennent les contraintes

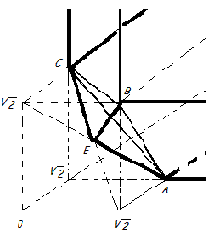
concernant l'avant derniere inégalite les eleves de seconde la demontrent en utilisant (a+b)/2>=sqrt(ab)
je doute que votre probleme soit de ce niveau

non il la démontre en écrivant simplement que (a - b)² 0

et en développant ....

Bonjour,
Toujours pas de solution au problème !

la condition (a+b)(b+c)(c+a)>8abc n'est pas équivalente à la relation initiale de l'exercice
De même la condition   n'est pas non plus équivalente à la relation initiale

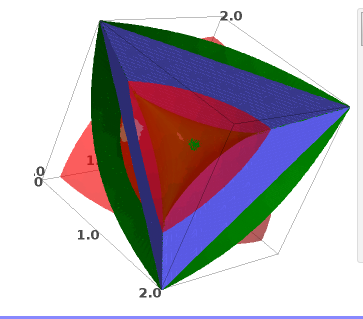
Une "preuve" graphique.

        

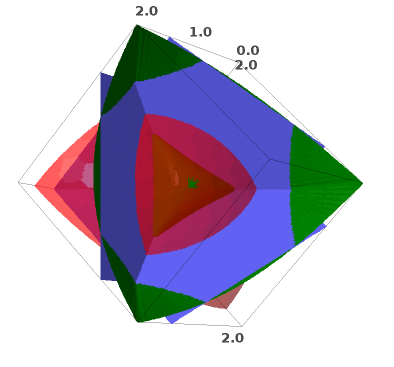
Le domaine est la portion de sphère rouge translucide découpée par les trois plans bleus.
La quantité dont on doit assurer la positivité s'annule sur la surface verte. Cette surface ne traverse pas le domaine, elle vient juste affleurer au centre du domaine (au point (1,1,1)).

Bon,


Si affleurement = tangence ,tu as fourni une belle
preuve graphique!


Pour un contrôle il faudrait, bien sûr, trouver une
algébrique démonstration.

Il est possible de construire certaines inégalités
en partant de  strictes égalités f(a,b,c) = g(a,b,c)
auxquelles en ajoute un LHS terme  


Ici,nous ne savons pas comment le problèmiste a procédé,



Alain

Pourquoi s'exprimer de cette affectée manière ?

Oui,


Par plaisir ou jeu ,la prochaine fois je te joindrai
un mien poème ,



Alain

Je mets ce lien pour ceux qui sont intéressés (qui ont le temps, l'envie et les capacités) :
C'est un cours assez complet sur les inégalités en général... Mais à part Jensen, je ne vois rien qui puisse se rapprocher de notre problème.
Mais vous serez peut-être plus inspirés que je ne le suis en cette période estivale.

Je ne savais pas que l'exercice allait être aussi difficile x)

Peux-tu dire d'où vient cette inégalité ? C'est un exercice posé quelque part ?

J'en ai aucune idée, c'est un ami à moi qui me l'a proposé car il n'y arrivait pas, mais je ne sais pas où il l'a eu...

Qu'advienne que pourra :

Bonjour,


Une autre piste?,simplifier le membre de droite:
et donc remplacer     par 3




Alain

Le début de réponse donné sur le site Les-mathematiques je l'ai démontré déjà il y a quelques jours (17-08-13 à 00:17 )... Mais je vois pas en quoi ça avance le truc.

Il faut avouer qu'avec les plans etc, c'est plus joli qu'avec les plan

[img1

bonjour,
Il me semble avoir trouvé une méthode ( toujours sous réserve...) dont je vous épargne les calculs.
Après avoir tourné en rond, je n'ai retenu que celle-ci, calculatoire et peu élégante.

La figure a été suffisamment décrite pour que je ne détaille pas trop la configuration du domaine.
Je reste fidèle à l'idée de considérer les plans X+Y+Z=S.
A(S,0,0);B(0,S,0);C(0,0,S)

H la projection othogonale de O sur (P).

(C) le cercle intersection de (P) avec la sphère SPH(0,R=).son centre est H.

Par définition du domaine on a .

"La borne de gauche vient d'un calcul simple".
Si alors le  cercle est entier, sinon Il y a 3 arcs de cercle de même mesure et centrés sur les sommets d'un triangle équilatéral.

Pour des raisons évoquées dans un autre post les expressions en jeu dans l'exercice sont des fonctions symétriques des variables a,b,c.

On peut donc etudier les variations  du produit V=abc    sur 1/3 du cercle seulement.
Notons I,J,K les milieux respectifs de AB,BC,CA

E ,E' F,F' G,G' les intersections respectives de CI,AI,BK avec le cercle.

Je définie un repère orthonormal direct (H, avec , Après quelques calculs liés au changement de repère... avec un paramètre angulaire

Quand M décrit cet arc, Je démontre que  abc=

En calculant ;
les expressions  de dépendantes de   et de permettent d'établir que sur les deux parties de l'arc G'F'  l'expression est maximum en  E, car décroissant sur l'arc GG'
.
Il suffit alors de vérifier qu'au point E  on a  S>3V². car S est par définition constante sur l'arc
Je rappelle que cette relation était suffisante  (voir post alexique )pour établir l'inégalité initiale proposé par yepa;

il est bon de remarquer qu'aux limites du domaine l'expression initiale de gauche devient infinie alors que reste finie.
pour cette raison, pour le raisonnement on reste strictement éloigné des bords.

Re bonjour,
En utilisant mes coordonnées et
il est aussi possible d'exprimer et démontrer que X'YZ+XY'Z+XYZ'<0 sur l'intervalle de défini plus avant;

Bon ben voilà :
Pas de déception pour ma part (si c'est correct bien sûr...)