- Cours sur les fonctions affines - troisième
- Cours sur les fonctions linéaires et les pourcentages - troisième
- Résolutions graphiques dans deux Exercices d'app. linéaires et trois d'app. affines - troisième
- Théorème de Thalès et réciproque - Cours Maths 3ème
- Révisions sur le calcul numérique - troisième
- Un Exercice sur la factorisation - troisième
- Trigonométrie dans les triangles rectangles : cosinus, sinus et tangente - troisième
- Identités remarquables, factorisation, développement - Cours 3ème
Fiche de mathématiques
Ile mathématiques > maths 3ème > Fonctions
 -2x.
-2x.
1.Calculer f(3), f(-2), f(7).
2.Quelles sont les images par f de -1, 6, 3/2 ?
3.Trouver le nombre qui a pour image 7.
1.Calculer f(-2), f(3) et f(10).
2.Quelles sont les images par f de 2/3, 1 et 7.
3.Trouver le nombre qui a pour image -2.
Déterminer son coefficient.
2.Quelles sont les images par f de -1, 6, 3/5 ?
3.Représenter graphiquement dans un repère orthonormal (O, I, J) la fonction linéaire f.
g est une fonction linéaire de coefficient 2/7;
j est une fonction linéaire de coefficient - 3/4;
l(x) = (x - 1)2 - (x2 + 1) = x2 - 2x + 1 - x2 - 1 = - 2x, l est donc une fonction linéaire de coefficent -2;
m(x) = x2 + 6x + 9 - x2 - 3x + 5 = 3x + 14, donc m n'est pas une fonction linéaire;
n(x) = 3(x -7) - 8x - 5 - 5(x + 4) = 3x - 21 - 8x - 5 - 5x - 20 = -10x - 46, donc n n'est pas une fonction linéaire.
Les fonctions h, i, k ne sont pas des fonctions linéaires.
2. f(-1) = -2 ×(-1) = 2 f(6) = -2 ×6 = -12 f([3/2]) = -2 × [3/2] = -3
3. Il faut donc trouver x tel que f(x) = 7, donc : -2x = 7, soit x = - 7/2
- 7/2 a pour image 7 par f.
1. f(-2) = - (3/2) ×(-2) = 3 f(3) = - (3/2) × 3 = - 9/2 f(10) = - (3/2) × 10 = - (3 × 5 × 2)/2 = -15
2. f(2/3) = - (3/2) × (2/3) = -1 f(1) = - (3/2) × 1 = - 3/2 f(7) = - (3/2) × 7 = - 21/2
3. Il faut donc trouver x tel que f(x) = -2, donc : -(3/2) x = -2, soit x = 4/3
4/3 a pour image -2 par f.
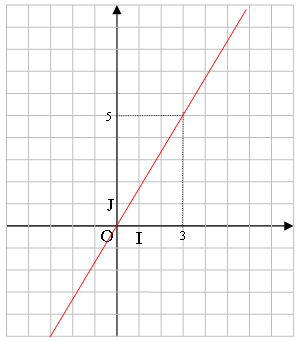
Or, f(3) = 5, donc : 3a = 5
Son coefficient a vaut 5/3
2. f(-1) = 5/3 ×(-1) = - 5/3 f(6) = (5/3) × 6 = (5 × 3 × 2)/3 = 10 f(3/5) = 5/3 × 3/5 = (5 × 3) /(3 × 5) = 1
3.
Fonctions Linéaires
exercice 1
Dans la liste des fonctions suivantes, donner celles qui représentent des fonctions linéaires. On précisera, dans ce cas, leur coefficient.exercice 2
Soit f la fonction linéaire définie par : x1.Calculer f(3), f(-2), f(7).
2.Quelles sont les images par f de -1, 6, 3/2 ?
3.Trouver le nombre qui a pour image 7.
exercice 3
Soit f la fonction linéaire de coefficient - 3/21.Calculer f(-2), f(3) et f(10).
2.Quelles sont les images par f de 2/3, 1 et 7.
3.Trouver le nombre qui a pour image -2.
exercice 4
1.f est une fonction linéaire définie par : f(3) = 5.Déterminer son coefficient.
2.Quelles sont les images par f de -1, 6, 3/5 ?
3.Représenter graphiquement dans un repère orthonormal (O, I, J) la fonction linéaire f.
exercice 1
f est une fonction linéaire de coefficient 4;g est une fonction linéaire de coefficient 2/7;
j est une fonction linéaire de coefficient - 3/4;
l(x) = (x - 1)2 - (x2 + 1) = x2 - 2x + 1 - x2 - 1 = - 2x, l est donc une fonction linéaire de coefficent -2;
m(x) = x2 + 6x + 9 - x2 - 3x + 5 = 3x + 14, donc m n'est pas une fonction linéaire;
n(x) = 3(x -7) - 8x - 5 - 5(x + 4) = 3x - 21 - 8x - 5 - 5x - 20 = -10x - 46, donc n n'est pas une fonction linéaire.
Les fonctions h, i, k ne sont pas des fonctions linéaires.
exercice 2
1. f(3) = -2 ×3 = -6 f(-2) = -2 ×(-2) = 4 f(7) = -2 ×7 = -142. f(-1) = -2 ×(-1) = 2 f(6) = -2 ×6 = -12 f([3/2]) = -2 × [3/2] = -3
3. Il faut donc trouver x tel que f(x) = 7, donc : -2x = 7, soit x = - 7/2
- 7/2 a pour image 7 par f.
exercice 3
f la fonction linéaire de coefficient - 3/2, elle s'écrit donc : f(x) = - 3/2x1. f(-2) = - (3/2) ×(-2) = 3 f(3) = - (3/2) × 3 = - 9/2 f(10) = - (3/2) × 10 = - (3 × 5 × 2)/2 = -15
2. f(2/3) = - (3/2) × (2/3) = -1 f(1) = - (3/2) × 1 = - 3/2 f(7) = - (3/2) × 7 = - 21/2
3. Il faut donc trouver x tel que f(x) = -2, donc : -(3/2) x = -2, soit x = 4/3
4/3 a pour image -2 par f.
exercice 4
1. On sait que f est une fonction linéaire, elle est donc de la forme : f(x) = axOr, f(3) = 5, donc : 3a = 5
Son coefficient a vaut 5/3
2. f(-1) = 5/3 ×(-1) = - 5/3 f(6) = (5/3) × 6 = (5 × 3 × 2)/3 = 10 f(3/5) = 5/3 × 3/5 = (5 × 3) /(3 × 5) = 1
3.

ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 Voir l'énoncé seul
Voir l'énoncé seul