- Bissectrice et cercle inscrit dans un triangle - Cours 4ème
- Exercice Bissectrices et cercles inscrits dans un triangle
- Cours sur les Figures planes, Distance d'un point à une droite et Tangente à un cercle
- QCM : Figures planes, distance et tangente - Exercice 4ème
- Six Exercices de géométrie pure - quatrième
Inscription / Connexion Nouveau Sujet
bonjour
a) construction de la figure
tracer un segment[ab] de 8 cm de longueur.placer son milieu o
tracer le cercle(c) de diametre [ab] et le cercle(c') de diametre [oa].
d est un point du cercle (c) tel que bd=3cm
la droite (do) recoupe le cercle (c') en e.
la perpendiculaire a la droite (ab) passant par le pont d coupe la droite (ae) en f.
la droite (fo) coupe la droite (ad) en g
b)raisonnement
1)a demontrer que les droites (de) et (af) sont perpendiculaires.
b en deduire que le point o est le point de concours des hauteurs du triangle adf.
c quelle est la nature du triangle oag ? JUSTIFIER LA REPONSE
D EN DEDUIRE QUE LE POINT G APPARTIENT AU CERCLE (c').
2) demontrer que le point g est le milieu du segment [ad].
3) en deduire que le triangle adf est isocele en f .
pour ce qui est de la figure je pense avoir reussi mais pour le raisonnement je n arrive pas a formule les phases merci pour votre aide
Bonjour dshijor
Je joins la figure correspondant à ce que j'ai compris.
Qu'as-tu fait? Donnes tes réponses et on corrigera s'il y a lieu.
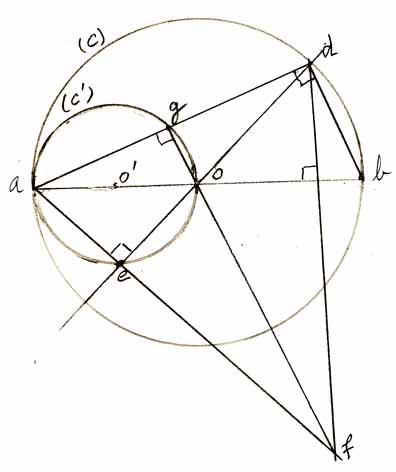
le schema que j ai fait est le meme
on sait que e est sur le cercle c'de diametre[oa]. f est le point de croissement de (df) et (ae) e appartient a la droite (af).
donc lesdroites (de)et(af) sont bien perpendiculaires
j espere que c est juste je pense mal formuler le reste je sais pas
Bonjour et bonne année
b) 1)a démontrer que les droites (de) et (af) sont perpendiculaires.
Considérons le triangle aoe, Son cercle circonscrit a pour diamètre ao c'est donc un triangle rectangle en e et ae (ou af) est perpendiculaire à eo (ou de)
Conclusion: (de) et (af) sont perpendiculaires.
b) en deduire que le point o est le point de concours des hauteurs du triangle adf.
On a vu que de est perpendiculaire à af et ab est perpendiculaire à df par construction; ces deux droites sont des hauteurs du triangle adf et leur point de concours est o
c) quelle est la nature du triangle oag ? JUSTIFIER LA REPONSE
Le triangle agf est rectangle en g, gf étant la 3 ème hauteur du triangle adf
Le triangle aog est donc rectangle en g
d) EN DEDUIRE QUE LE POINT G APPARTIENT AU CERCLE (c').
Pour les mêmes raisons que le triangle aoe, g appartient au cercle (c') (ao diamètre du cercle circonscrit) .
2) demontrer que le point g est le milieu du segment [ad].
Considérons le triangle aod
ao=od= rayon du cercle (c), ce triangle est donc isocèle et comme og est perpendiculaire à ad; og est hauteur et médiane, donc g est le milieu de ad
3) en deduire que le triangle adf est isocele en f .
g étant le milieu de ad, la hauteur fg est également médiane, donc le triangle adf est isocèle en f, et af=df
Je ne sais pas si c'est la meilleure démonstration, la géométrie n'est pas mon point fort.


