Inscription / Connexion Nouveau Sujet
brevet amérique du nord,juin 2006
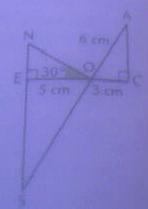
On sait que:
EO= 5cm , OC=3cm et OA=6cm
les points E, O et C sont alignés.
Les triangles ENO et OCA sont rectangles respectivement en E et en C.
La droite (AO) coupe la droite (NE) en S.
a) j'ai déja repondu a cette question
b) montrer que les droites (NS) et (AC) sont parallèles
calculer les valeurs exactes de OS et de ES.
c) calculer ON sachant que NOE=30° arrondir au mm.
d) calculer l'angle COA.
démontrer que le triangle SON est rectangle.
(j'aimerais bien un petit coup de main si vous pouvez pas me donnez les réponses je voudrais des explication svp merci )
b) (NE) est perpendiculaire a (EC) et (AC) l'est également or nous savons que deux droites perpendiculaires à une même troisième sont parallèles. Et S appartient à (NE) donc (NS) est bien parallèle à(AC)
c) cos = OE/ON
 ON=OE/cos
ON=OE/cos
d)cos= CO/OA
donc =
(CO/OA)
bonsoir,
b) le triangle OCA est rectangle en C
donc les droites (OC) et (CA) sont perpendiculaires
Les points E, O, et C étant alignés, par conséquent les droites (EC) et (AC) sont perpendiculaires
Le triangle ENO est rectangle en E
donc les droites (NE) et (EO) sont perpendiculaires
Les points E, O, et C étant alignés et le point S appartenant à la droite (NE), par conséquent les droites (NS) et (EC) sont perpendiculaires
Les droites (NS) et (AC) sont donc perpendiculaires à la même droite (EC)
Elles sont donc parallèles entre elles
calculer les valeurs exactes de OS et de ES.
Dans les triangles OAC et OES :
les points A, O, S et C, O, E sont alignés dans le même ordre
les droites (ES) et (AC) sont parallèles
D'après le théorème de Thalès :
OA/OS = OC/OE = AC/ES donc 6/OS = 3/5 = 3 3/ES
3/ES
par conséquent
OS = 6 x 5 / 3 = 10 cm
ES = 5 x 3 3 / 3 = 5
3 / 3 = 5 3
3
c) calculer ON sachant que NOE=30° arrondir au mm.
Dans le triangle ONE rectangle en E on a :
cos NOE = OE/ON
ON = OE / cos NOE
= 5 / cos 30°
ON = 5,8 cm au mm près
d) calculer l'angle COA.
Dans le triangle COA rectangle en C on a :
cos COA = OC/OA
soit cos COA = 3/6 = 1/2
COA = 60°
démontrer que le triangle SON est rectangle
Les angles EOS et COA sont opposés par le sommet
donc EOS =COA = 60°
On a :
SON = NOE + EOS
Soit
SON = 30° + 60° = 90°
Le triangle SON possède un angle droit il est donc rectangle en O
A+
pour kesar
b) (NE) est perpendiculaire a (EC) et (AC) l'est également or nous savons que deux droites perpendiculaires à une même troisième sont parallèles. Et S appartient à (NE) donc (NS) est bien parallèle à(AC)
(y a t-il pas des calculs a faire?)
non en tout cas je l'aurais fait sans calcul c'est un des théorèmes qu'on apprend en 6eme
mais bon après je ne vois pas comment tu peux faire par calcul
donc ça te prendras du temps
en maths il faut être rapide et efficace (cf laurha l'as fait sans Thalès également)
n'oublies pas que tu as du temps imparti lors du brevet et que parfois cela se joue sur des détails comme ceux là..
bah ouais vu que Thalès est un rapport de proportionnalité il faut que tu connaisses les longueurs non?
mais je ne vois vraiment pas où tu veux en venir.
en tout cas il n'y a pas besoin de Thalès pour démontrer que (NS) et(AC) sont parallèles


