Inscription / Connexion Nouveau Sujet
Cos 45°, sin 45°, tan 45°
Bonjour,
j'ai un petit problème pour un exercice, merci pour votre aide:
On sait que:
Démontrer que cos 45° = sin 45° = .
Merci encore 
Bonjour.
Quel est le problème?
cos(45°) = 5 / (5 2)
2)
= 1 /  2
2
= 1* 2 / (
2 / ( 2*
2* 2)
2)
=  2 / 2
2 / 2
Comme le côté adjacent et le côté opposé sont égaux, sin(45°) est aussi  2/2
2/2
Johnny
Bonsoir,
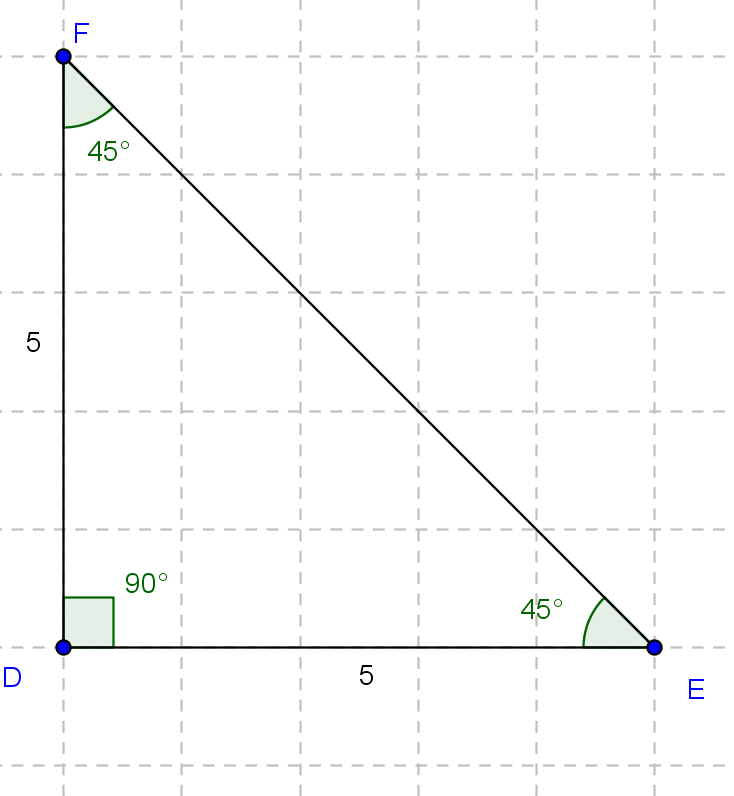
cos(DEF)=cos(45°)=DE/FE
sin(DFE)=sin(45°)=DE/FE
d'où cos(45°)=sin(45°)
cos(45°)=sin(45°)=DE/FE
FE=
cos(45°)=sin(45°)=
Pour résoudre ton problème tu dois tout d'abors svoir les 3 regles
cos : coté adjacent/ hypothénuse
sin : coté opposé sur hypothénuse
tan : coté opposé / adjacent
ensuite pour prouver que sin 45 = cos 45 = racine carrée /2
il te faut résoudre 2 calculs
cos E et sin F soit cos 45 et sin 45, n'oublie pas que tu ne dois jamais laisser de racine carré dans le dénominateur c'est la clef de l'exercice!!!!!


