Inscription / Connexion Nouveau Sujet
Difficultés pour un DM...
Bonsoir,
Depuis ce matin j'ai beaucoup de mal à résoudre un exercice de mon DM. En effet, il y a deux questions que je ne parviens pas à traiter, en espérant que quelqu'un ici éclairera ma lanterne, merci !
On donne la figure ci-dessous, qui n'est pas en vraie grandeur et qui n'est pas à reproduire.
Les points M, O et Q sont alignés ainsi que les points N, O et P. Les segments [OM] et [OQ] sont des diamètres des deux cercles tracés ;
on donne : OM = 7,5 cm et OQ = 4,5 cm.
1. Prouver que le triangle MNO est rectangle en N.
On admet pour la suite que le triangle OPQ est rectangle en P.
2. Justifier que les droites (MN) et (PQ) sont parallèles.
Jusqu'ici, pas de problème, seulement c'est là que tout se corse :
3. Prouver que les angles NMO et PQO sont égaux.
Je sais que par une symétrie orthogonale, une symétrie centrale, une translation, une rotation, l'image d'un angle est un angle de même mesure, mais il ne me semble pas que la réponse soit de ce côté là...
4. En supposant que ON=5cm, calculer OP (là, aucun problème)
Calculer la mesure de l'angle NMO ? Comment faire ? En calculant le sinus ?
Merci beaucoup de m'avoir lue !
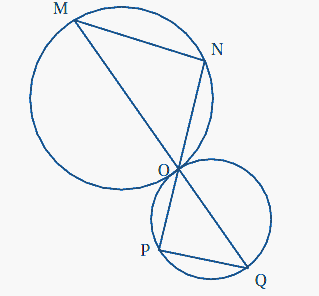
bonsoir
que penses-tu des angles MON et QOP ?
on a aussi MNO = OPQ = 90°
en considérant les triangles MNO et PQO (Somme des angles 180°) ....
Les angles MON et QOP me paraissent égaux car opposés par le sommet, non ?
Je ne vois pas réellement comment utiliser le fait que la somme des angles d'un triangle vaut 180° dans la mesure où nous n'avons la mesure que d'un angle par triangle (MNO = OPQ = 90°)... Ou alors je ne vois pas comment me servir du fait que MON=QOP
En tout cas, merci beaucoup de t'être intéressé au sujet !
oui , ils sont opposés par le sommet
donc MON = QOP
la somme des angles d'un triangle = 180°
donc MON + MNO + NMO = QOP + OQP + OPQ = 180°
comme MNO = OPQ = 90°
on peut retirer MNO et OPQ l'égalité reste vraie
comme MON = QOP
on peut retirer MON et QOP l'égalité reste vraie
l'égalité finale est donc NMO = OQP
Ah, j'ai compris ! Merci infiniment ! (:
Et concernant le calcul de l'angle NMO, en considérant que ON = 5cm; j'en suis arrivée à la démarche suivante :
SinNMO= 5/7,5 = 2/3
Arcsin(2/3) = 41,8103149
Donc l'angle NMO vaut environ 41,8°
Est - ce juste ?



