Inscription / Connexion Nouveau Sujet
Etude d'une longueur variable
Bonjour,
J'ai un devoir maison à rendre pour cette semaine et ayant des difficultés en maths j'aimerais que quelqu'un puisse m'aider.
Merci
Etude d'une longueur variable.
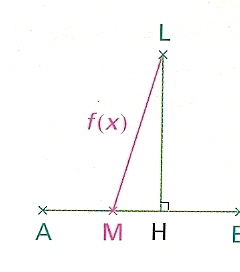
Sur la figure ci-contre :
AB = 5 cm, AH = 3 cm et LH = 4 cm.
Un point M mobile se déplace sur le segment [AB].
La distance LM varie alors en fonction de la distance AM.
On pose x = AM et f(x) = LM.
1) a. Faire une figure avec x = 0 et calculer f(0).
b. Faire une figure avec x = 1 et calculer f(1).
c. Déterminer f(3).
d. Pourquoi a-t-on f(5) = f(1)? En déduire f(5).
2) Quel est l'ensemble de définition de la fonction f?
3) Uniquement par des considérations d'ordre géométrique, déterminer le sens de variation de f, puis dresser le tableau de variations de f.
4) a. Démontrer que : pour tout réel x appartenant à [0 ; 3], f(x) = V(x² - 6x + 25).
b. Démontrer que : pour tout réel x appartenant à [3 ; 5], f(x) = V(x² - 6x + 25).
c. En déduire l'expression de la fonction f sur tout l'ensemble de définition de f.
5) a. Dresser un tableau de valeurs de f avec un pas de 0,25.
b. Construire sur papier millimétré, la courbe représentative de f (on prendra 2 cm pour l'unité sur chaque axe).
Faire apparaître, sur les axes de coordonnées, les informations obtenues dans les questions 1) et 2). Indiquer aussi une équation de la courbe.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Merci d'avance à la personne qui pourra m'orienter.
Bonjour,
Je pense que si x=0 alors LM est confondu avec LH et que f(0)=0 mais je suis vraiment pas sûr.
Je me pencherais plus demain sur le problème.
b. J'ai aussi utilisé Pythagore pour trouver f(1) et je trouvre (en arondissant) f(1) = 4,5.
c. Les points M et H sont confondus car AM = 3 et AH = 3 donc LH = LM
f(3) = 4
d. Pour f(1) et f(5) MH = 2
Donc f(1) = f(5)
Donc f(5) = 4,5
2. Df = [A;B]
Je ne suis pas du tout sur.
3. Geographiquement :
f est croissante quand f(x)
 f(3)
f(3)
f est decroissante quand f(x)
 f(3)
f(3)
Tableau :
x : 0 3 6
f(x): 5 (fleche qui monte) 4 (fleche qui descend) 0
Pour ce qui est de la question 4 je ne vois pas comment le demontrer et la question 5 je ne vois pas qu'elle est l'equation de la courbe et les coordonnées des questions 1 et 2.
J'ai aussi utilisé Pythagore pour trouver f(1) et je trouve (en arrondissant) f(1) = 4,5.
Attention, au niveau seconde, on n'arrondit pas.
f(1) = V20 = 2V5
2) Quel est l'ensemble de définition de la fonction f?
ce sont tous les x possibles, donc [0;5]
3. Geographiquement :
f est croissante quand f(x) f(3)
f est decroissante quand f(x) f(3)
Tableau :
x : 0 3 6
f(x): 5 (fleche qui monte) 4 (fleche qui descend) 0
Comment la flèche peut monter en passant de 5 à 0 ...
Ta fonction est décroissante jusqu'à x=3 puis croissante
On ne va pas jusqu'à 6 car le segment ne fait que 5 cm
Merci pour votre aide.
Cependant, je bloque sur la question 4) en effet, je ne sais pas comment m'y prendre pour demontrer l'equation.
Avec pythagore :
pour x entre 0 et 3
LM² = MH² + HL²
LM = V((3-x)² + 4²)
= V(9 - 6x + x² + 16)
= V(x² - 6x + 25)
f(x) = V(x² - 6x + 25)
Ok merci.
J'ai essayer de la meme facon pour le b. seulement je ne trouve pas sa :
Pour x entre 3 et 5
LM² = HB+HL²
LM = V((2-x)² +4²)
LM = V(4-4x+x²+16)
LM = V(x²-4x+20)
J'ai du ne pas mettre la bonne longueur mais je ne vois pas pourquoi. Merci de m'éclairer.
bonjour,
Moi aussi j'ai cette exercice pour demain comme DM je ne comprend pas le 4.
Repondez SVP
Merci