Inscription / Connexion Nouveau Sujet
Etude de fonction
Bonsoir et merci pour vos réponses.
Soit la fonction f:x (x-a)*ln(x-a). Où a est une constante.
(x-a)*ln(x-a). Où a est une constante.
1) Calculer f' et f''.
f'=ln(x-a)+1
f''=
2)Montrer que le graphe de f ne possède pas de point d'inflexion, quelle que sois la valeur de la constante a.
Alors la je bloque un peu, si j'ai bien compris ce que j'ai lu sur les points d'inflexion. Le numérateur de la dérivée seconde ne peut s'annuler dons le graphe de f ne possède pas de point d'inflexion quelle que soit la valeur de a.
Je suis pas sûre de la justification.
Bonjour
les points d'inflexion sont des points d'abscisse x telle que f"(x) = 0. (condition nécessaire, pas suffisante)
et 1/blabla n'est jamais nul, parce que blabla*0 = 0 différent de 1, quel que soit blabla
Bonjour à vous Lafol et Carpediem.
Donc cela donnerai pour tout x différent de a, 1/(x-a) ne peut s'annuler donc le graphe de f ne possède pas de point d'inflexion.
C'est ca
Je n'ai pas bien compris ce passage:
"parce que blabla*0 = 0 différent de 1, quel que soit blabla"
lafol voulait dire que si 1/A vaut 0 alors par produit en croix 1=A*0.
Ce qui est faux. Donc 1/A ne s'annule pas.
Bonsoir Alb12
Désolée si je suis un peu lente mais c'est la première fois que je vois cette notion.
Moi j'ai noté en premier qu'il n'y avait que le numérateur que ne pouvait s'annuler. En fait
c'est tout f'' qui ne peut s'annuler c'est ca la nuance?
la condition nécessaire (mais pas suffisante) pour avoir un point d'inflexion d'abscisse x est que f"(x) = 0
que f"(x) soit une fraction ou pas, c'est bien de f"(x) qu'il s'agit et pas d'un éventuel numérateur de f"(x) ....
3) trouver la valeur de a pour laquelle le graphe de f possède un point à tangente horizontale d'abscisse égale à 2/e.
Je sais que le coefficient directeur d'une droite horizontale est 0 mais pour le reste je comprends pas ou je dois aller 

la condition nécessaire (mais pas suffisante) pour avoir un point d'inflexion d'abscisse x est que f"(x) = 0
que f"(x) soit une fraction ou pas, c'est bien de f"(x) qu'il s'agit et pas d'un éventuel numérateur de f"(x) ....
ouais enfin la tu chipotes un peu ...
f" est une fraction !!
f" = 0 <=> numérateur de f" = 0 <=> 1 = 0 <=> absurde ...
mais tu as raison quelque part car :
3) trouver la valeur de a pour laquelle le graphe de f possède un point à tangente horizontale d'abscisse égale à 2/e.
ne veut pas dire grand chose ... alors est-ce l'énoncé exact ?
3/ f dépend d'un paramètre a ....
la courbe de f admet une tangente horizontale <=> f'(x) = 0 ...
tu résous cette équation et tu exprimes x en fonction de a ...
or tu sais que x = 2/e ... donc tu peux déterminer la valeur du paramètre a correspondant ...
j'ai eu l'impression que ahl1700 pensait qu'il fallait que f" soit un quotient et que la condition ne portait que sur le numérateur dudit quotient, c'est pour ça que j'ai précisé. C'est clair que quand f" est un quotient, dire que ce quotient est nul ou dire que son numérateur est nul, c'est à peu près équivalent (cas de nullité du dénominateur à considérer pour une équivalence mieux que "à peu près")
Je me suis mal exprimée, cela me semblait logique que si le numérateur ne pouvait s'annuler tout f'' ne pouvait s'annuler aussi. Mais cela m'apprendra à être plus précise 
Oui Carpediem c'est bien l'énoncé exact. C'est pour cela que j'ai rien capté."un point à tangente horizontale d'abscisse égale à 2/e." Ca veut dire quoi :?
:?
Donc si je suis bien se que tu dis je dois résoudre f'=.
Ce qui donne:
a=1/e
oui, c'est bien ça
--> tangente horizontale te dit que la dérivée doit valoir 0
--> et on te dit que cela se passe au point d'abscisse 2/e
d'où ton équation qui te permet de trouver a
(ce qui te donne une courbe, celle obtenue pour a =1/e)
dont tu vas être sûre qu'au point d'abscisse 2/e, la courbe admettra une tangente horizontale...
ta résolution est juste
Salut merci Malou c'est plus clair, la formulation était un peu tordue.
4)Pour toute la fin du problème, on pose a=1/e.
a) Domaine de définition.
Df=] ;+
 [
[
b) Tableau des signes et de variations.
f(x)=
f'(x)=
oui, voilà
la question 4 est l'étude de fct obtenue pour a=1/e
et tu retrouves bien la tangente horizontale pour x=2/e
cela me semble OK
attention : il faut mettre une double barre verticale en 1/e ...
certes la fonction s'y prolonge par continuité mais à-priori elle n'y est pas définie ....
La fonction n'est pas définie sur 1/e, autant pour moi Carpediem.
5) Etablir l'équation de la tangente t au graphe f, sachant que la pente de t est égale à 1.
Cela voudrait dire que f'(x)=1
Ce qui donnerai:
La fonction n'est pas définie sur 1/e, autant pour moi Carpediem.
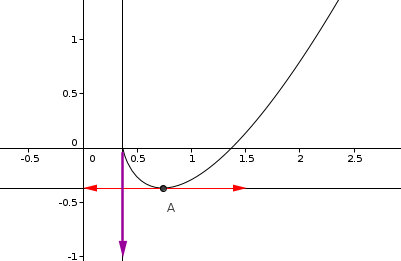
et tête baissée....je n'ai rien vu, toutes mes excuses...et donc oublie aussi effectivement la demi-tangente violette !
bien vu carpediem !
malou : no problemo ... 
T:y=
C'est ca

peut-être ...
mais ces calculs sont trop compliqués (!!) pour moi
calcule d'abord f(1 + 1/e) et f'(1 + 1/e) (enfin ici inutile car on sait que ça fait 1)
puis ensuite remplace dans la formule de l'équation de la tangente
...
Alors pour que ce soit plus digeste:
T:y=f'(a)(x-a)+f(a) avec a =
On sait que f'(a)=1
y=
C'est quoi une demi-tangente?
la moitié d'une tangente 
disons, une fct définie en 0 et à droite de 0 peut admettre une demi-tangente à droite de 0
exemple
la fonction racine carrée
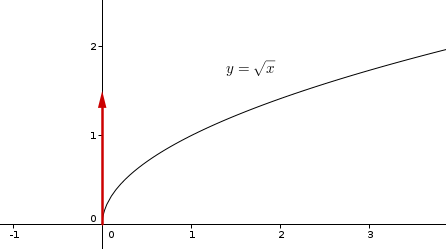
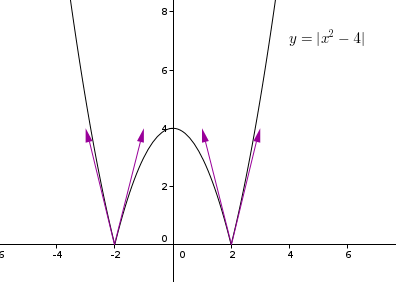
et en voilà une qui a 4 demi-tangentes
exemple : au point d'abscisse -2, les deux demi-tangentes ne sont pas dans le prolongement l'une de l'autre (coefficient directeur différents, on a ce qu'on appelle un point anguleux), et on n'a pas de tangente en ce point
(idem pour x=2)
demi-tangente= moitié de la tangente, j'aime cette idée, les maths c'est pas si compliqué
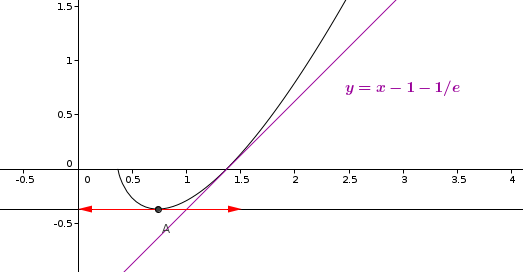
Plus sérieusement si on me dit prouver que la droite d'équation y=x-1-1/e est demi-tangente a cf.
ben tu ne peux pas vraiment...parce que ce n'est pas le cas ! 
cela serait le cas si par exemple ta fonction n'avait été définie que sur [1+1/e ; + [
[
alors là tu aurais eu une demi-tangente à droite du point d'abscisse 1+1/e
la demi-tangente provient par exemple d'une non dérivabilité en un point comme la fct racine carrée en 0, (on trouve un coeff directeur infini, d'où une demi-tangente portée par l'axe des ordonnées)
ou bien par une non dérivabilité en un point comme x=2 sur le dessin de 21h48
le nombre dérivé à droite de 2 vaut 4
le nombre dérivé à gauche de 2 vaut -4
-->ces deux nombres dérivés ne sont pas égaux
-->donc f n'est pas dérivable en 2, donc elle n'admet pas de tangente en x=2
par contre elle admet 2 demi-tangentes, une à droite de coeff directeur +4 et une à gauche de coeff directeur -4
d'où le point anguleux
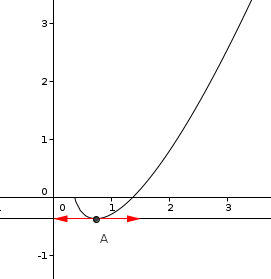
6) On considère la surface S, délimitée par le graphe de f, l'axe des abscisse et les droites
et x=2.
Hachurer cette surface sur votre graphique, puis calculer son aire.
Il me semble que c'est une intégration par partie.
Donc je devrais prendre:
donc
et
donc
C'est ok jusque là?
Donc je devrais prendre:
et
n'oublie pas de dire aussi que sur l'intervalle considéré ta fct ne prend que des valeurs positives (pour justifier ton calcul d'aire)
quand je vois que entre
et
je prends toujours :
que je ne transforme surtout pas
mais surtout
qui simplifie évidemment le calcul vu les bornes données

ce n'est pas égal...ce sont deux primitives différentes de la même fonction (elles diffèrent d'une constante)
si tu as
et que tu désires le dériver...tu vas bien retrouver le en appliquant (u²)'=2u*u'
essaie
--> carpediem, je viens d'apprendre que les {}{} n'étaient pas indispensables dans le code...ben ça alors....
Oui c'est vrai si je dérive je retrouve x-1/e.
Mais quelle est la reflexion pour en arriver là. Désolée je chipote un peu mais j'aime tout comprendre.
--> carpediem, je viens d'apprendre que les {}{} n'étaient pas indispensables dans le code...ben ça alors....
oui les accolades ne sont nécessaires que lorsque l'argument contient plus d'un caractère ...
ainsi
\vec umais
\vec {AB}
Oui c'est vrai si je dérive je retrouve x-1/e.
Mais quelle est la reflexion pour en arriver là. Désolée je chipote un peu mais j'aime tout comprendre.

ben c'est la lecture du tableau des dérivées (lu dans l'autre sens)
u*u' est la dérivée de 1/2*u²
donc 1/2*u² est une primitive de u*u' (et ici u'=1)
oui ?
Ce que je veux dire c'est que moi pour la primitive de je trouve
, c'est un raisonnement très mécanique, je n'aurai jamais su trouver
et c'est vrai que cela simplifie les calcul.
Pour le calcule d'intégrale je trouve ca, mais je sais plus quoi faire avec.
Désolée pour la photo mais je n'arrive pas à écrire cela avec le latex.
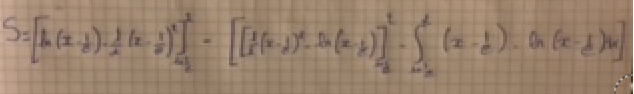
***image agrandie***
non, je ne comprends pas pourquoi tu as 3 morceaux...
sous le signe intégral, tu ne devrais plus avoir de log
RQ : sous l'intégrale, tu as u'*v que j'ai simplifié



 en terminale
en terminale