Inscription / Connexion Nouveau Sujet
fonction logarithme et algorithme
Bonjour,
Voici mon exercice de maths :
Partie A :
On considère la fonction g définie sur [1;+infini[ par g(x) = ln x - (1/2).
1) Etudier le sens de variation de g sur [1;+infini[.
2) Résoudre l'équation g(x) = 0 dans [1;+infini[.
3) En déduire que g(x) > 0 si, et seulement si, x > V(e).
Partie B :
On considère la fonction f définie sur [1;+infini[ par f(x) = 2x² (ln x - 1) + 2.
1) On appelle f' la fonction dérivée de la fonction f sur l'intervalle [1;+infini[.
a) Montrer que pour tout nombre réel x de l'intervalle [1;+infini[, f'(x) = 4x g(x).
b) Etudier le signe de f'(x) sur [1;+infini[ et en déduire le sens de variation de f sur [1;+infini[.
2) a) Montrer que, dans l'intervalle [2;3], l'équation f(x) = 0 admet une solution unique notée a.
b) Déterminer un encadrement d'amplitude 10-2 de a.
3) L'algorithme ci-contre permet de déterminer un encadrement de la solution a. (J'ai la calculatrice Ti83+)
Entrées
Saisir a, b et p trois nombres réels tels que 2 ≤ a < b ≤ 3 et p > 0.
Traitement
Tant que f(a) * f(a + p) > 0 et a + p ≤ b, a prend la valeur a + p.
Fin Tantque
Sortie
Afficher "La solution est dans l'intervalle [a;a+p]"
a) Préciser le rôle des variables a, b et p.
b) Expliquer l'instruction "Tant que f(a) * f(a + p) > 0"
c) Appliquer l'algorithme avec a = 2, b = 3 et p = 0,1.
d) Quelles valeurs faudrait-il saisir pour a, b et p afin que l'algorithme retourne l'encadrement trouvé à la question précédente?
e) L'algorithme tel qu'il a été écrit suppose que la solution appartient à l'intervalle [a;b] saisi en entrée.
Modifier l'algorithme de sorte que s'il n'y a pas de solution dans cet intervalle, une phrase bien choisie soit retournée.
Voici ce que j'ai fait :
Partie A :
1) g(x) = ln(x) - -1/2 sur [1 ;+∞[
g'(x) = (1/x)
(1/x) > 0 car si x appartient à [1 ;+∞[ alors x est toujours supérieur à 0 alors g'(x) est toujours supérieur à 0 alors g(x) est toujours croissante.
2) g(x) = 0
ln(x) - (1/2) = 0
ln(x) = 0,5
eln(x) = e0,5
x = e0,5
x = V(e)
3) g(x) > 0
ln(x) - (1/2) > 0
ln(x) > 0,5
eln(x) > e0,5
x > e0,5
x > V(e)
Partie B :
1) a) f(x) = 2x² (ln x - 1) + 2
f'(x) = 4x * (ln(x) - 1) + ((1/x) * 2x²)
f'(x) = 4x * (ln(x) - 1) + (2x²/x)
f'(x) = 4x * (ln(x) - 1) + 2x
f'(x) = 4x * ln(x) - 4x + 2x
f'(x) = 4x (ln(x) - (1/2))
b) f'(x) est négatif sur [1 ;Ve ] et positif sur [Ve;+∞[.
Donc f(x) est décroissante sur [1 ; Ve] et croissante sur [Ve ;+∞[.
2) a) L'équation f(x) = 0 n'admet qu'une solution sur [2 ;3] car elle est strictement croissante sur [2 ;3].
b) 2,20 < a < 2,30
3) a) a, b et p permettent de déterminer pour quelle valeur entre 2 et 3 f(x) = 0.
b) Cette instruction signifie que quand f(a) * f(a + p) < 0, l'algorithme ne sera plus valable.
c) : Prompt A, B, P
: 2 ≤ A < B ≤ 3
: P > 0
: If A * (A + P) > 0 et A + P ≤ B, A → A + P
: End
: Disp “La solution est dans l'intervalle A, A + P”.
d) Il faudrait saisir a = 2,2, b = 2,3 et p = 0.
e) : Prompt A, B, P
: 2 ≤ A < B ≤ 3
: P > 0
: If A * (A + P) > 0 et A + P ≤ B, A → A + P
: Else
: Disp “La solution est dans l'intervalle A, A + P, sens inverse, A”
: End
Est-ce que quelqu'un pourrait me corriger s'il vous plaît? Merci d'avance.
Bonne fin de journée.
a méditer
Va-t-il accepter cela ?
pourquoi utiliser V(e) au lieu de e0,5 dans la réponse ?
2) a)
b) 2,20 < a < 2,30 un encadrement d'amplitude 10-1 ou 10-2 ?
3) a) a, b et p permettent de déterminer pour quelle valeur entre 2 et 3 f(x) = 0.
non, mal dit et insuffisant .
b) Cette instruction signifie que quand f(a) * f(a + p) < 0, l'algorithme ne sera plus valable. 
d) Il faudrait saisir a = 2,2, b = 2,3 et p = 0. 
p>0 a = 2 b =3 et p =10-2
bref: revoir "Théorème des valeurs intermédiaires"
avez-vous algobox ? ou autre ?
[lien]
ALGOBOX :
CODE DE L'ALGORITHME :
1 VARIABLES
2 a EST_DU_TYPE NOMBRE
3 b EST_DU_TYPE NOMBRE
4 p EST_DU_TYPE NOMBRE
5 DEBUT_ALGORITHME
6 AFFICHER "2 ≤ a < b ≤ 3 et p > 0"
7 TANT_QUE (a<2 ou a>=b ou b>3 ou p<=0) FAIRE
8 DEBUT_TANT_QUE
9 LIRE a
10 LIRE b
11 LIRE p
12 FIN_TANT_QUE
13 SI (F1(a)*F1(b)<0) ALORS
14 DEBUT_SI
15 TANT_QUE (F1(a)*F1(a+p)>0 ET a+p<=b) FAIRE
16 DEBUT_TANT_QUE
17 a PREND_LA_VALEUR a+p
18 FIN_TANT_QUE
19 AFFICHER "La solution est dans l'intervalle ["
20 AFFICHER a
21 AFFICHER " ; "
22 a PREND_LA_VALEUR a+p
23 AFFICHER a
24 FIN_SI
25 SINON
26 DEBUT_SINON
27 AFFICHER "Il n'y a pas de solution dans l'intervalle ["
28 AFFICHER a
29 AFFICHER " ; "
30 AFFICHER b
31 FIN_SINON
32 AFFICHER "]"
33 FIN_ALGORITHME
34
35 Fonction numérique utilisée :
36 F1(x)=2*pow(x,2)*(log(x)-1)+2
RÉSULTATS :
***Algorithme lancé***
2 ≤ a < b ≤ 3 et p > 0
Entrer a : 2.3
Entrer b : 2.4
Entrer p : 0.01
Il n'y a pas de solution dans l'intervalle [2.3 ; 2.4]
***Algorithme terminé***
Généré par AlgoBox
RÉSULTATS :
***Algorithme lancé***
2 ≤ a < b ≤ 3 et p > 0
Entrer a : 2
Entrer b : 3
Entrer p : 1e-4
La solution est dans l'intervalle [2.2184 ; 2.2185]
***Algorithme terminé***
Généré par AlgoBox
a tester en mode pas à pas
Merci de votre aide et désolé, je me suis mal exprimé, par "corriger", je voulais dire "vérifier et me dire où je me suis trompé pour que je puisse me corriger".
Bonne journée
Avez-vous compris le "Théorème des valeurs intermédiaires" ?
Pour comprendre algorithme vous pouvez faire un copiez coller dans algobox et le faire tourner pas à pas. (ou je vous l'envoie par mail, voir mon profil)
Le but est de comprendre, pas d'avoir la bonne réponse.
"2) a) Montrer que, dans l'intervalle [2;3], l'équation f(x) = 0 admet une solution unique notée a."
L'équation f(x) = 0 admet une solution unique car ...
re bonjour,
voici ce que je pense être bon après votre aide. Pourrez-vous vérifier s'il vous plaît? Merci d'avance.
2) a) L'équation f(x) = 0 n'admet qu'une solution sur [2 ;3] car elle est strictement croissante sur [2 ;3] et comme f(2) < 0 et f(3) > 0, il y a bien une seule et unique valeur sur cet intervalle en laquelle f(x) = 0.
b) 2,21 < a < 2,22
3) a) a, b et p permettent de déterminer pour quelle valeur entre 2 et 3 f(x) = 0, a étant la valeur minimale que doit prendre f(x) = 0, b la valeur maximale et p étant obligatoirement positif.
b) Cette instruction signifie que l'algorithme ne marchera que quand f(a) * f(a + p) > 0.
Bonne fin de journée
si f(
)=0
Pouvez-vous expliquez simplement ce que fait l'algorithme ?
attention dans l'algorithme a
où se trouve quand f(a)>0 et f(a + p) >0 (si c'est possible!)
où se trouve quand f(a)<0 et f(a + p) <0 (si c'est possible!)
donc
où se trouve quand f(a) * f(a + p) > 0 (si c'est possible!)
où se trouve quand f(a)>0 et f(a + p)<0 (si c'est possible!)
où se trouve quand f(a)<0 et f(a + p) >0 (si c'est possible!)
donc
où se trouve quand f(a) * f(a + p) < 0 (si c'est possible!)
Vous pouvez utiliser Géogébra [lien]
en tapant f(x) = 2x² (ln x - 1) + 2 dans la ligne de saisie pour voir la courbe et réfléchir.
Vous pouvez utiliser Géogébra [https://www.ilemaths.net/annu/site-geogebra.html ]
en tapant f(x) = 2x^2* (log( x) - 1) + 2 dans la ligne de saisie pour voir la courbe et réfléchir.
re bonjour,
j'ai regardé avec geogebra et j'ai remarqué que dans l'intervalle [0;1], la fonction est positive mais décroissante. Ensuite, dans l'intervalle [1;1,6], la fonction est négative et décroissante. Après, dans l'intervalle [1,6;2,22], la fonction est négative mais croissante. Et enfin, dans l'intervalle [2,22;+infini[, la fonction est croissante. Ainsi, à partir de ces observations, je pense que l'algorithme sert à calculer les coordonnées des points. Pourrez-vous me confirmer mon idée, s'il vous plaît? Merci d'avance.
f croissante sur [e0,5 ; +
[
pour i et j 
[e0,5 ; +[
si i
j alors f(i)f(j)
ou
si f(i)>f(j) alors i>j
donc
si f(3)>f()=0 alors 3>
pour p>0
si f(3)>f()=0 et f(3+p)>f()=0 alors 3>
de même
si 0>f(a+p) et 0>f(a) alors >a+p et >a
donc 
[a;a+p]
ensuite on essaye pour a+p et a+2p (a'=a+p et a'+p=a+2p)
puis
a"=a+k*p et a"+p=a+(k+1)*p jusqu'au moment où f(a")<0 et f(a"+p)>0 alors [a";a"+p]
merci pour votre aide. Donc si j'ai bien compris, les réponses sont celles-ci :
3) a) a, b et p permettent de déterminer pour quelle valeur entre 2 et 3 f(x) = 0, a étant la valeur minimale que doit prendre f(x) = 0, b la valeur maximale et p étant obligatoirement positif.
b) Cette instruction signifie que l'algorithme ne marchera que quand f(a) * f(a + p) > 0 et que quand f(a) * f(a + p) < 0, il se passera autre chose.
d) Il faudrait saisir a = 2,2, b = 2,3 et p = 10-2.
Pouvez-vous vérifier s'il vous plaît? Merci d'avance.
si f()=0
attention dans l'algorithme a
où se trouve quand f(a)<0 et f(a + p) <0
donc
où se trouve quand f(a) * f(a + p) > 0
où se trouve quand f(a)<0 et f(a + p) >0
donc
où se trouve quand f(a) * f(a + p) < 0
"a étant la valeur minimale que doit prendre f(x) = 0"
non, x peut prendre la valeur a mais pas "f(x) = 0"
"b)..."
"d) Il faudrait saisir a = 2,2, b = 2,3 et p = 10-2."
d'après l'énoncé, savez que la solution est entre 2 et 3, vous n'avez pas d'argument pour choisir 2,2 et 2,3 plutôt que 2,5 et 2,9 ou une autre zone de recherche plus petite que [2;3]
Vous n'avez toujours pas compris ce que fait l'algorithme!
Entre a et b, on avance à chaque tour de boucle de p et on teste si [a",a"+p] si c'est faux on continue la boucle, si c'est vrai on sort de la boucle et on répond [a",a"+p]
(a"=a+k*p et a"<b)
bonjour,
merci pour votre aide. J'ai réfléchi et essayé de comprendre ce que vous voulez dire et je pense que ça signifie pour la question 3) a) cela :
a, b et p permettent de trouver la valeur où f(x) = 0, l'intervalle dans lequel on se place étant [a ;b] et p étant la valeur que doit prendre le tour de boucle.
Pourrez-vous me le confirmer s'il vous plaît? merci d'avance.
p étant la valeur que l'on ajoute à a à chaque tour de boucle.
p est le pas de l'incrémentation de la variable a pour la boucle "tant que"
voir:
En pratique, on découpe le segment [a;b] en petits segments de longueur p et on recherche dans quel petit segment se trouve la solution de f(x)=0.
merci donc pour la question 3) b), je pense que c'est ça :
Cette instruction signifie que l'algorithme ne marchera que quand f(a) * f(a + p) > 0 et que quand f(a) * f(a + p) < 0, il faudra mettre une autre instruction.
Est-ce que vous pouvez vérifier si c'est ça s'il vous plaît? Merci d'avance.
On ne demande pas de corriger l'algorithme (qui marche bien) et de mettre une autre instruction.
SVP répondez à mon message : Posté le 30-04-13 à 16:52
"où se trouve ..."
merci
quand f(a) < 0 et f(a + p) < 0, a se trouve en-dessous de 0.
quand f(a) * f(a + p) > 0, a se trouve en-dessous de 0.
quand f(a) < 0 et f(a + p) > 0, a se trouve au-dessus de 0.
quand f(a) * f(a + p) < 0, a se trouve au-dessus de 0.
Je pense que c'est ça mais j'ai un gros doute.
oui, un gros doute 
est sur l'axe des x et entre a et b
et comme a>0 (et b>0) alors >0
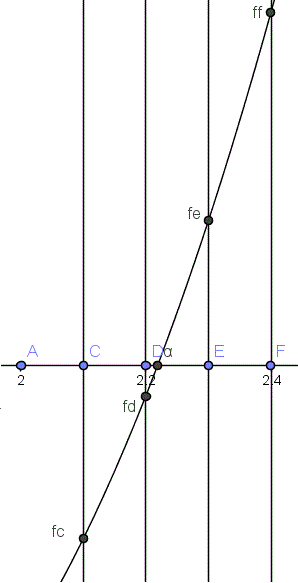
f(C) est négatif donc C<
f(D) est négatif donc D<
f(E) est positif donc < E
f(F) est positif donc < F
merci pour votre aide. Je pense d'après vos explications que la réponse à la question de la partie B du 3) b) est :
Cette instruction signifie que la réponse que l'algorithme va nous donner est toujours supérieure à 0.
Pourrez-vous me confirmer mon hypothèse s'il vous plaît? Merci d'avance.
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_des_valeurs_interm%C3%A9diaires
Cas particulier (Théorème de Bolzano) :
si f(a) et f(b) ne sont pas de même signe, il existe au moins un réel c compris entre a et b tel que f(c) = 0 (car 0 est compris entre f(a) et f(b)).
en l'occurrence :
si f(a) et f(a+p) ne sont pas de même signe, il existe au moins un réel c compris entre a et a+p tel que f(c) = 0 (car 0 est compris entre f(a) et f(a+p)).
f(a)*f(a+p)<0
f(a) et f(a+p) ne sont pas de même signe
donc
si f(a)*f(a+p)<0 , il existe au moins un réel
compris entre a et a+p tel que f() = 0 (car 0 est compris entre f(a) et f(a+p)).
la condition de sortie de boucle est donc f(a)*f(a+p)
0 ,
inversement, la condition pour rester dans la boucle est donc f(a)*f(a+p)>0
d'où l'instruction "Tant que f(a) * f(a + p) > 0"
Annuler
connectez vous