Inscription / Connexion Nouveau Sujet
Image et relation d'ensemble
Soit X un ensemble non vide une image
on défini une relation sur X ~ de telle sorte :
a) Montrer que la relation est équivalente :
Réflexivité : (x)=(x)
Symmetrie : (x)=(y) et (y)=f(x)
Transivité : (x)=(y) et (y)=(z) donc (x)=(z)
jusque là ça va
b) Montrer qu'il existe exactement une image :
telle que
Montrer qu'il existe exactement une image :
cette question n'a pas grd sens !!!
la question qui aurait un sens serait
montrer qu'en posant pour tout x
on définit bien une application sur l'ensemble des classes d'équivalence
autrement dit si x et x' sont ds la meme classe (, a-t-on f(x)=f(x')?
Peut-être mais comme c'est la question posée çA m'intéresse peut de savoir si elle a du sens et je sais pas pour m'y prendre
Je comprends mieux ! c'est une traduction et je ne sais pas l'allemand
mais je crois deviner tout de meme
Voici une traduction plus conforme
Soit X un ensemble non vide une application
on défini une relation sur X ~ de telle sorte :
a) Montrer que la relation est équivalente :
Réflexivité : (x)=(x)
Symmetrie : (x)=(y) et (y)=f(x)
Transivité : (x)=(y) et (y)=(z) donc (x)=(z)
jusque là ça va
b) Montrer qu'il existe exactement une application :
telle que
on definit par un choix arbitraire de x dans la classe. il faut verifier que si l'on fait un autre choix x' on aboutit au meme resultat
autrement dit
Cette question signifie
si x et x' sont ds la meme classe ([x]_{/ \sim}=[x']_{/ \sim}), a-t-on f(x)=f(x')?
La reponse est evidemment oui par def de la relation d'equivalence

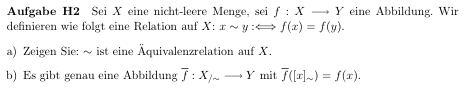

 algèbre en post-bac
algèbre en post-bac