Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths spé AlgèbreTopics traitant de algèbre [tout]Lister tous les topics de mathématiques
Niveau maths spé
Le seigneur des anneaux (4/7): Anneaux simple et artinien.
Posté par 1 Schumi 1
Bonjour à tous, 
Un exo vraiment tordu:
Citation :
Montrer qu'un anneau est simple et artinien à gauche si et seulement si il est égal à l'anneau)
des matrices n*n sur un certain corps k (non nécessairement commutatif) et que de plus n et k sont uniques.
Pour cela, on pourra commencer par démontrer la proposition suivante appelée lemme du double centralisateur: soit A un anneau simple, I un idéal à gauche de A,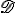
l'anneau des applications A-linéaires de I, considérées comme opérant à droite sur I (ie, des applications 
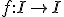telles que (x+y)f=xf+yf et (ax)f=a(xf) pour tous x,y de I et a dans A, en notant xf l'image de x par f) et 
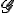l'anneau des applications 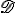-linéaires considérées comme agissant à gauche sur I (ie, des applications 
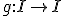telles que g(x+y)=gx+gy et g(xf)=(gx)f pour tous x,y de I et f dans 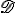, en notant gx l'image de x par g); alors l'application canonique 
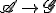qui à a associe la multiplication à gauche par a ()
), est un isomorphisme d'anneaux.
Montrer qu'un anneau est simple et artinien à gauche si et seulement si il est égal à l'anneau
Pour cela, on pourra commencer par démontrer la proposition suivante appelée lemme du double centralisateur: soit A un anneau simple, I un idéal à gauche de A,
Bravo pour l'endurance!
Bon on commence par le lemme du double centralisateur: ladite application est clairement un morphisme.
L'injectivité se règle simplement (haha, très drôle...).
Pour la surjectivité ça se corse un peu. Voici l'idée:
On prend g dans
Et après, ô miracle on trouve que g(x)=g(1)x donc problème résolu.
Et le truc dont j'ai besoin précisemment, ben, ça ressemble étrangement à la deuxième condition qu'on a sur G si on prend f(x)=xa. Le problème c'est que ça ne définit pas forcément une application de I dans I. Donc bref, j'essaie de bidouiller un peu une application qui me permette de prouver que g(xa)=(gx)a pour x dans I, a dans A et xa dans I mais c'est pas gagné...
Une idée?
Annuler
connectez vous
algèbre en post-bac