Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup AlgèbreTopics traitant de algèbre [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

matrice et projection

Posté par
robby3 10-01-10 à 22:01

Bonsoir tout le monde,
je bute sur une question:

Citation :
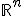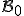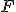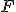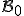Dans \mathbb{R}^n munie de sa base canonique \mathcal{B}_0 orthonormée pour le produit scalaire canonique, on considère un sous-espace  F de dimension r donné par une "matrice génératrice" P\in\mathcal{M}_{n,r}(\mathbb{R}),donc les colonnes de P sont les vecteurs d'une base de F exprimé dans  \mathcal{B}_0.
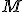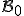Montrer que la matrice M dans \mathcal{B}_0 de la projection orthogonale sur 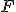F est donnée par M=P(^tP.P)^{-1}.^tP \\


j'ai montré que M était la matrice d'un projecteur et que celle ci est orthogonale ssi ^tM=M,ce qui est le cas, il me reste à montrer que c'est la projection sur F...

j'ai seulement réussi à montrer que Im(M)\subset F en remarquant que les colonnes de M soient combinaisons linéaires de celle de P.
Pouvez-vous m'aider à conclure s'il vous plaît?
Merci d'avance.

Posté par
monrow Posteur d'énigmesre : matrice et projection 10-01-10 à 22:25

Salut

Quel est le rang de M ?

Posté par
robby3re : matrice et projection 10-01-10 à 22:30

Salut,
le rang de M c'est r non?
or r=dim(F) d'ou l'égalité Im(M)=F...d'ou le résultat?

Posté par
monrow Posteur d'énigmesre : matrice et projection 10-01-10 à 22:31

Citation :
le rang de M c'est r non?


Pourquoi?

Posté par
robby3re : matrice et projection 10-01-10 à 22:39

bah,parce que c'est logique et que ça m'arrange...
mise à part ça,je vois pas trop...serait-ce la même valeur que le rang de P?
et les colonnes de P sont des vecteurs de base de F(de dimension r).

Posté par
monrow Posteur d'énigmesre : matrice et projection 10-01-10 à 22:43

D'accord

Est ce que tu peux déjà donner juste une inégalité entre rg(M) et r?

Posté par
robby3re : matrice et projection 10-01-10 à 22:47

oui, rang(M)\le r puisque Im(M) est inclus dans F.
si je ne me trompe pas.

Posté par
monrow Posteur d'énigmesre : matrice et projection 10-01-10 à 22:49

D'accord. Que vaut MP?

N'oublie pas que 3$\rm rg(AB)\le min(rg(A),rg(B))

Posté par
robby3re : matrice et projection 10-01-10 à 22:52

MP=P
et
r=rang(P)=rang(MP)\le min(rg(M),rang(P))

non?

Posté par
monrow Posteur d'énigmesre : matrice et projection 10-01-10 à 22:54

Si !

donc : 3$ r\le min(rg(M),r), donc 3$ rg(M) \ge r et hop t'as ce que tu veux

Posté par
robby3re : matrice et projection 10-01-10 à 22:55

ok,merci Monrow!

Posté par
monrow Posteur d'énigmesre : matrice et projection 10-01-10 à 22:55

aucun problème

Posté par
robby3re : matrice et projection 10-01-10 à 22:56

oui,j'ai "tilté"...
désolé,j'avais vraiment pas "vu",seulement senti.
Merci et bonne soirée!

Posté par
monrow Posteur d'énigmesre : matrice et projection 10-01-10 à 22:57



Bonne soirée !


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !