Salut !

A priori j'aurais pensé à l'inégalité de Cauchy-Schwarz, mais pas sûr !

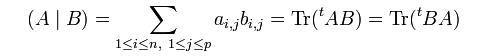
Bonjour,

En diagonalisant A avec une matrice de passage orthogonale on se ramène au cas où A est de plus diagonale. Les inégalités sont alors presque immédiates.

Bonjour !

J'ai essayé avec Cauchy-Schwarz et j'obtiens :

|(A|B)| (A|A)(B|B)

Ce qui donne :

tr(tAB) tr(tAA) tr(tBB), cependant, je ne vois pas comment continuer ...

Je vais essayer avec la méthode de la diagonalisation !

Je n'arrive pas à avancer avec la méthode de la diago, pouvez-vous me donner une piste SVP ?

puisque A et B sont des matrices symétriques alors tA = A et tB = B

j'obtiens donc 0 tr(AB) tr(AA)tr(BB)

comment conclure que tr(AB) tr(A)tr(B) ? Merci d'avance !

Bonjour jandri !

Exploite plutôt l'idée de jandri, qui est bien meilleure, puisqu'on aura alors tr(A) = tr(D) où D est diagonale, ça simplifie pas mal les calculs !

ok, donc ça donne :

A = PDP^-1 mais je ne vois pas comment trouver une inégalité à partir d'une diagonalisation !

Si au départ tu as des matrices diagonales, tu as à montrer que



ce qui est vrai si tes coefficients sont positifs, non ?

Sauf erreur.

Dans la partie de droite la somme est double sur i et j.

Salut

Avec de la congruence simultanée, il me semble que ça marche tout seul non? Genre, on commence par supposer A définie positive.
On applique le théorème à spectral à B dans (R^n,q) où q est la forme quadratique définie positive associée à A^(-1).
On blablatte un peu et il me semble que quelques lignes de calcul donne le résultat...

On conclut par densité.

On peut supposer que les matrices sont diagonales parce que symmétriques, ensuite on ne sait pas si elles sont définies positives, on sait juste qu'elles sont positives.

Ok, quand tu parles de densité tu parles des matrices définies positives denses dans les positives, mais en fait on peut s'en sortir directement.

Merci pour vos réponses !

Je n'ai pas très bien saisie la méthode de la congruence simultanée, pas vue en cours ...;

mais le passage par une matrice diagonale puis en utilisant les sommes me paraît plus simple, reste à trouver le point de départ !

Quel point de départ, il me semble que l'exercice est complétement résolu, non ?

Bonjour,

Je pensais avoir été assez clair.
On diagonalise A avec une matrice de passage P orthogonale (P^-1=^tP):
P^-1AP=D (diagonale à coefficients0) et P^-1BP=^tPBP=C (matrice symétrique et positive: ^tXCX=^tX^tPBPX=^tYBY0 avec Y=PX).
Tr(A)=Tr(D), Tr(B)=Tr(C) et Tr(AB)=TR(DC).
Tr(DC)=d_iic_ii est positif car d_ii0 et c_ii=(e_i|g(e_i)0.
Tr(D)Tr(C)=d_iic_iid_iic_ii car tous les nombres sont positifs.

Bonjour,

Merci pour votre réponse, justement je venais de trouver une chose similaire .

Pour finir, je dois montrer que tr(AB+BA)² 4trA²trB²

en utilisant encore les sommes, on a :

( aii bii + bii aii )² = (aii² bii² + 2 aii bii bii aii + bii² aii²)

Or, on a montré précédemment que aii bii aiibii
d'où aii²bii² aii² bii²
de même pour bii²aii²
et 2 aii bii bii aii 2 aii²   bii²

en sommant le tout on obtient bien (aii bii + bii aii)² 4 aii² bii²

Est-ce exact ?

Merci encore !

Ce n'est pas exact car la trace de (AB+BA)² n'est pas égale à .

Si on s'est ramené au cas où A est diagonale, la matrice C=AB+BA a pour terme général d'où:

.

remarque: pour cette inégalité on utilise seulement le fait que A et B sont symétriques (pas nécessairement positives).

d'accord, merci beaucoup