Inscription / Connexion Nouveau Sujet
Produit scalaire dans un repère orthonormé 1ère S
Bonjour 
J'ai un devoir de niveau 1ère S sur les produits scalaires dans un repère, ce répère étant orthonormé.
Voici l'énoncé :
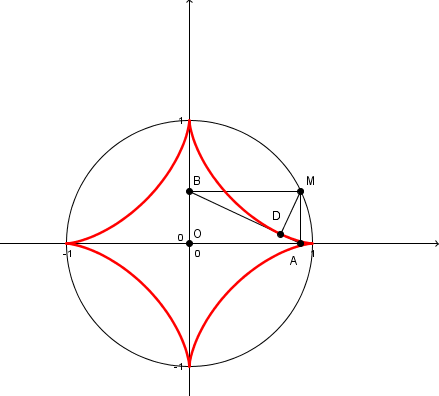
Le plan est muni d'un repère orthonormé d'origine O.
C est le cercle de centre O et de rayon 1.
M est un point quelconque du cercle C.
Les points A et B sont les projetés orthogonaux respectifs du point M sur l'axe des abscisses et sur l'axe des ordonnées.
Le point D est le projeté orthogonal du point M sur la droite (AB).
J'ai joint à ce post une figure.
1) Démontrer que .
=OB²
Ici, j'ignore comment décomposer le vecteur, mais je pense qu'il faut également utiliser le théorème de Pythagore
2) En déduire que AD = OB², puis =
Cette question devrait la suite de la précédente...
3) On note les coordonnées du point M. Démontrer que les coordonnées de D sont
Je ne sais pas du tout la réponse à cette question, peut-être y a-t-il une formule à appliquer ?
Merci 
Bonjour,
une figure dans un cas particulier pour un point M quelconque n'est pas un bon plan
mieux serait de choisir un point M autre que le point pi/4 de ce cercle trigo !!!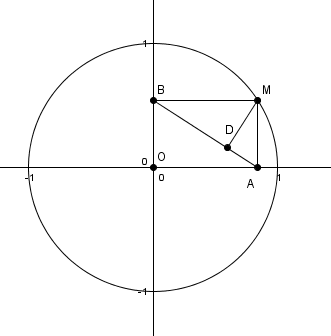
M étant la projection orthogonale de B sur (AM) (OAMB est en fait un rectangle !!) on a (cours) etc
puis D étant la projection de M sur (AB) on a ce même produit scalaire qui est aussi égal à etc)
remarque : Pythagore n'a rien à faire là quand on parle de vecteurs :
Pythagore se démontre à partir du produit scalaire !!
La dernière question est une conséquence directe de la formule du produit scalaire à partir des coordonnées des vecteurs et des questions précédentes.
les coordonnées d'un point P sont par définition les nombres x et y
***scorie effacée***
ignorer la dernière scorie qui était en dehors de l'écran quand j'ai fait POSTER et qui aurait dû être effacée
(début d'une explication ratée)
Merci d'avoir fourni une meilleure figure, j'avais en effet mal placé M
Pour la 1), il faut utiliser une propriété telle que :
Dans un parallélogramme (marche également pour un rectangle), et
Donc, cela se traduit sur la figure par .
M étant la projection orthogonale de B sur (AM), donc =
.
=
=
=
=
Est-ce bon ?
oui.
sauf qu'il est inutile (et même néfaste vu qu'on a un point D dans la figure) de dire ce qu'il se passe dans "un parallélogramme ABCD" en général alors que le notre s'appelle AMBO
il suffit de dire que AMBO étant un parallélogramme (un rectangle) etc
Merci pour la 1.
puis D étant la projection de M sur (AB) on a ce même produit scalaire qui est aussi égal à \vec{AB}.\vec{AD}
Pour la 2), je n'arrive pas à "visualiser les projetés", d'autant plus qu'il faut garder
AD = OB²
Comme OB = AM et que OB² = AM², peut-être qu'il faut s'orienter sur ces côtés ?
Comme il y a marqué "En déduire", je suppose qu'il faut utiliser les réponses de la question 1, mais je ne vois pas comment...

c'est vrai que ce n'est pas trop évident à trouver cette méthode avec des produits scalaires...
surtout qu'il faut que je recommence tout vu que ça date d'il y a 15 jours !!
cette question 2 est assez simple :
mais AD = 1 !!! (rectangle, AB = OM = 1 cercle de rayon 1)
maintenant on utilise la question 1 pour "en déduire" (de ces deux façons d'écrire le produit scalaire ) la relation demandée pratiquement juste en l'écrivant ... (= de façon instantanée)
ensuite la deuxième formule ... : remarquer que
il suffit donc en partant de AD = OB² de justifier du signe
(= de justifier que A,B,D sont alignés et M est toujours entre A et B, ce qui est par construction vrai ou "assez évident")
Désolé pour le temps mis à répondre 
J'arrive maintenant à comprendre un peu mieux,
comme on sait (à ce stade) que = OB², on ne doit garder que
avec les projetés.
mais AD = 1 !!!
Ici, ce ne serait pas plutôt AB ?
Enfin, pour la deuxième formule, tu parles de la question qui suit ?
Le signe est positif puisque que c'est un carré, après je ne sais pas du tout.
oui c'est AB =1
dans la question 2 il y a deux parties
- montrer que AD = OB²
- puis
je parle du signe qui distingue à partir de
AD = OB² * AB (en longueurs) de savoir si en vecteurs on a
ou bien
signe (à choisir) qui dépend du sens des deux vecteurs.
et donc de l'alignement (pour avoir le droit de passer en vecteurs, il faut qu'ils soient colinéaires) et de D entre A et B ou à l'extérieur (sens des vecteurs = signe)
montrer que AD = OB²
C'est ce que l'on vient de faire précédemment.
oui c'est AB =1
ou bien
Cela reviendrait à dire
Pour ce qui est de la colinéarité des vecteurs, on doit utiliser la projection, comme par exemple D est le projeté de M sur (AB) ?
Comme AB = 1, les calculs sont dans la continuité de la question précédente, qu'était AD = OB² ?
la colinéarité est triviale par construction : le point D est sur la droite (AB) par construction, de l'énoncé lui même.
il suffit juste de le dire dans la rédaction.
je ne comprend pas ton autre interrogation
de la seule colinéarité on en déduit que soit l'une (avec +) soit l'autre (avec -) et rien ne permet de dire à ce stade laquelle des deux serait la bonne !!
et le fait que D soit entre A et B
donne le sens des vecteurs et donc permet de choisir lequel est le signe correct.
et pareil il suffit de le dire dans la rédaction
et ces "petits truc anodins" doivent être dit explicitement dans la rédaction, sinon ça ne prouve rien du tout.
Comme D est le projeté orthogonal de M sur (AB), alors D [AB] (par construction)
On en déduit que les points A, D et B sont alignés et par conséquent, les vecteurs sont colinéaires.
Je sais qu'il y a deux sens disponibles, mais je pense qu'il faut utiliser
Je trouve cela étrange, car en "suivant" et
, c'est positif verticalement (on se déplace vers le haut) et négatif horizontalement (on se déplace vers la gauche).
Je voulais dire dans mon autre interrogation que comme on a réussi à déduire précédemment que AD = OB², et que , cela ne change rien dans
.
Ça y est : comme les points A et B sont de part et d'autre de D, on doit utiliser 
Je viens enfin de comprendre, j'ai oublié de réutiliser cette propriété, désolé
ce que tu as compris est exactement le contraire de ce qui est !!
(et en plus de ce qu'on te demande de prouver dans l'énoncé lui-même)
et ça c'est parce que tu rates complètement la signification de ce qu'est un vecteur et la différence entre nombres et vecteurs
est absurde, un vecteur ne peut pas être égal à un nombre.
et il ne faut pas utiliser ce qu'on demande de démontrer !!
utiliser ce qu'on doit démontrer pour le démontrer n'a jamais rien démontré du tout.
en plus tes histoires de vers le haut etc c'est du pipeau
M appartenant au cercle (entier) ces sens varieront selon la position de M
par contre on aura toujours D entre les points A et B
et donc les vecteurs et
seront toujours de même sens (ou au pire nuls)
et donc par conséquent la relation qu'il faut choisir n'est pas
mais bien , comme demandé par l'énoncé.
ça fait un peu enfonçage de porte ouverte, parfaitement, parce que c'est "assez évident",
mais c'est cela qui doit être clairement présent à l'esprit
et exprimé clairement dans une vraie démonstration rigoureuse.
Le truc c'est que je n'arrive pas à faire le parallèle avec le cours pour écrire une démonstration rigoureuse.
Puisque est vecteur et n'est pas un nombre (
), qu'est-ce qui nous donne le droit de l'ajouter pour passer de :
AD = OB²
à
?
car
, pas de vecteurs là dedans
maintenant et
sont colinéaires (sur la droite (AB) et de même sens (car D est entre A et B)
donc il existe un nombre réel k > 0 (de même sens !!) tel que
et cette relation vectorielle se traduit par en longueurs , vu que k est positif
en comparant avec le facteur réel k > 0 est égal à
et par conséquent
voila une rédaction détaillée toute cuite.
Merci beaucoup pour cette explication, en fait, c'est simplement la propriété de la colinéarité des vecteurs, donc (presque) rien à voir avec le produit scalaire à proprement parler si j'ai bien compris  .
.
le produit scalaire c'était pour démontrer les trucs d'avant
trucs qui ont servi maintenant pour "en déduire" la dernière relation vectorielle qui est effectivement "juste que de la colinéarité"
3) On note (x,y) les coordonnées du point M. Démontrer que les coordonnées de D sont(x^3,y^3)
D'abord, graphiquement, cela a l'air faux.
Puisque M a pour coordonnées
On doit utiliser les coordonnées des vecteurs
et
De plus, est-ce que cela doit s'écrire sous la forme (je donne un exemple) :
oui
et "graphiquement ça a l'air faux" est ... faux
graphiquement ça a l'air plausible
quand x ou y =  1, x3 ou y3 valent bien
1, x3 ou y3 valent bien  1 et D est bien en l'un des points d'intersection du cercle avec les axes
1 et D est bien en l'un des points d'intersection du cercle avec les axes
idem pour x ou y = 0 vu que quand l'un vaut 0 l'autre vaut forcément  1
1
sinon x et y sont forcément < 1 en valeur absolue (cercle de rayon 1 !!)
et donc |x^n| < |x| quel que soit x et pareil pour y
et c'est parfaitement cohérent avec la position de D par rapport à celle de M
c'est à peu près tout ce qu'on peut tirer de "graphiquement"
non
c'est une astroïde.
mais de toute façon ce n'est pas ce qu'on demande.
on demande uniquement de prouver au final que si les coordonnées de M sont (x;y) alors celles de D sont (x^3; y^3) et c'est tout
et c'est la suite du calcul précédent et rien d'autre.
coordonnées du vecteur AB en fonction de x et y
valeur de OB² en fonction de x et y (facile OB = y, donc OB² = y²)
donc coordonnées de AD en fonction de x et y
et les coordonnées de A en fonction de x et y étant connues (facile aussi : A(x; 0))
on en tire les coordonnées de D et c'est tout
il faut en fait ne pas oublier que M n'est pas un point n'importe où dans le plan, de coordonnées (x; y) absolument quelconques, mais un point du cercle, et donc que x² + y² = 1
on peut donc remplacer là où ça nous arrange y² par 1-x² etc ...
(juste quelques lignes de calcul en tout, ni droites ni courbes ni rien que du calcul pur à partir de la dernière relation)
avec toutes ces variables ça fait pas mal fouillis et ça noie pas mal le poisson.
je te proposais de virer définitivement et complètement tes xA, xB etc
et de tout écrire directement en fonction de x et y et de rien d'autre.
B a pour coordonnées (0; y) (trivial)
donc on n'écrit pas de (xB; yB) on écrit directement (0; y) pour ce point
etc
mais les calculs doivent certainement revenir au même
perso je laisse OB² = y² et c'est tout, c'est plus propre pour obtenir l'ordonnée de D = l'ordonnée de A (0) plus l'ordonnée de B (y) multipliée par OB² = y² et donc en une demi ligne de tête l'ordonnée de D = y3
et ça évite tous tes développements compliqués.
ce n'est que pour l'abscisse de D qu'il faut remplacer y² par 1-x²
(démontré directement par Pythagore comme tu as fait mais une fois ce Pythagore rédigé c'est fini, on a la relation x² + y² = 1 et on en fait ensuite ce qu'on veut comme ça nous arrange sans revenir à ds noms de points)
et le développement quasiment de tête aussi :
vu que (de tête) le x-xy² obtenu directement et quasiment de tête de l'abscisse de D devient x(1-y²) = x3 quasiment de tête (en tout cas en l'écrivant directement sur la feuille de papier)
l'exo est donc terminé
il y aurait plein de choses à dire à propos de la courbe décrite par le point D quand M parcourt le cercle
comme je l'ai mentionné cette courbe s'appelle une astroïde et on la trouve dans des endroits les plus divers (portes de garages ou de bus, glissement d'une échelle le long d'un mur, point d'un cercle qui roule à l'intérieur d'un autre etc)
on peut démontrer que la droite AB est la tangente en D à cette courbe
et s'amuser pour observer tout ça avec Geogebra (en animant le point M) :