Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths spé AlgèbreTopics traitant de algèbre [tout]Lister tous les topics de mathématiques
Niveau maths spé
Réduction et fonction
Posté par gui_tou
Bonjour
J'ai besoin d'un petit coup de main pour cet exo
Citation :
Soient![3$E=\mathcal{C}^{\infty}([0,1],{\bb R})](https://latex.ilemaths.net/ile_tex.cgi?3$E=\mathcal{C}^{\infty}([0,1],{\bb R})) et
et 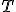 l'endomorphisme de
l'endomorphisme de 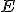 qui à
qui à 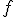 associe
associe ![3$T(f)\ :\ x\in[0,1]\to{4$\fr12\[{3$f}\(\fr{x}{2}\)+{3$ f}\(\fr{x+1}{2}\)\]](https://latex.ilemaths.net/ile_tex.cgi?3$T(f)\ :\ x\in[0,1]\to{4$\fr12\[{3$f}\(\fr{x}{2}\)+{3$ f}\(\fr{x+1}{2}\)\])
a. Soient et
et ![3$x\in[0,1]](https://latex.ilemaths.net/ile_tex.cgi?3$x\in[0,1]) . Calculer
. Calculer }(f)(x)) .
.
b. Soit . Calculer
. Calculer }(f)(0)) .
.
c. Soient et
et ![3$x\in[0,1]](https://latex.ilemaths.net/ile_tex.cgi?3$x\in[0,1]) . Calculer
. Calculer }(f)(x)) .
.
d. Montrer que 1 est valeur propre de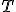 et trouver le sous-espace propre associé.
et trouver le sous-espace propre associé.
e. Est-ce que , avec
, avec  peut être valeur propre de
peut être valeur propre de 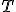 ?
?
f. Calculer)') .
.
g. Déterminer le sous-espace propre associé à la valeur propre
Soient
a. Soient
b. Soit
c. Soient
d. Montrer que 1 est valeur propre de
e. Est-ce que
f. Calculer
g. Déterminer le sous-espace propre associé à la valeur propre
a. Par une récurrence immédiate,
b. Avec, pour tout entier
c. Même chose,
d. Il suffit d'exhiber une fonction
Donc
L'espace propre associé à la valeur propre 1 est l'ensemble des fonctions
C'est une zolie équation fonctionnelle, je n'ai pas encore trop réfléchi à sa résolution mais j'aurais envie de dire que ses solutions sont les fonctions constantes sur [0,1].
Du coup,
e. Supposons
f. Sauf erreur,
g. Ce sous-espace est l'ensemble des fonctions de E qui vérifient
Je ne crois pas savoir résoudre ce bidule

-----------------------------------------------------
Ce serait sympa si vous pouviez m'aider à résoudre les équations fonctionnelles, et à vérifier si je n'ai pas dit trop de bêtises !
Merci

Salut 
Je ne trouve pas du tout la même chose que toi à la 1).  Perso, je trouve une somme de Riemann ce qui me convient assez, à savoir:
Perso, je trouve une somme de Riemann ce qui me convient assez, à savoir:
A vérifier, mais je pense avoir bon.




 algèbre en post-bac
algèbre en post-bac