Fiche de mathématiques
Ile mathématiques > maths 1ère > Fonctions : généralités
Dans chacun des exercices 1 à 6, f désigne une fonction définie sur l'intervalle I.
Montrer que f est bornée sur I.
 = \dfrac{1}{x + 1})
 et
et 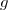 de
de 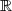 vers
vers 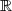 définies par :
définies par :  = 3x -5 \text{ et } g(x) = \dfrac{2x^2 + 1}{x^2 + 1}) .
.
1. a) Montrer que pour tout nombre réel ,
,  = 1 + \dfrac{x^2}{x^2 + 1})
b) Montrer que pour tout nombre réel ,
,  = 2 - \dfrac{1}{x^2 + 1})
c) En déduire que pour tout nombre réel ,
,  \leq 2) .
.
2. La fonction est elle bornée sur
est elle bornée sur 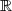 ?
?
3. Démontrer que la fonction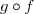 est bornée sur
est bornée sur 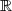 .
.
4. Démontrer que la fonction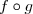 est bornée sur
est bornée sur 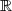 et que pour tout nombre réel
et que pour tout nombre réel  ,
, (x) < 1) .
.
Si x I, alors :
I, alors :
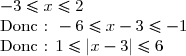 .
.
D'où : f est bornée sur I.
Si x I, alors :
I, alors :
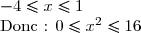
D'où : f est bornée sur I.
si x I, alors :
I, alors :
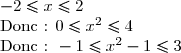
Donc f est bornée sur I.
Si x I, alors :
I, alors :
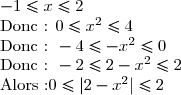
Donc f est bornée sur I.
Si x I, alors :
I, alors :
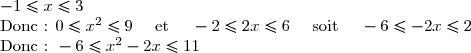
D'où : f est bornée sur I.
 = \dfrac{1}{x + 1}) ; I = [0; 3].
; I = [0; 3].
Si x I, alors :
I, alors :
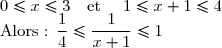
D'où : f est bornée sur I.
)
1. b) Pour tout réel x, on a :
 - 1}{x^2 + 1} = \dfrac{2x^2 + 1}{x^2 + 1} = g(x))
1. c) Pour tout réel x, = 1 + \dfrac{x^2}{x^2 + 1}) .
.
Or, pour tout x réel, x² et x² + 1 sont positifs, donc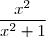 est positif et par conséquent : g(x)
est positif et par conséquent : g(x) 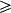 1.
1.
Pour tout réel x, = 2 - \dfrac{1}{x^2 +1 }) .
.
Or, pour tout réel x,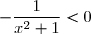 , donc : g(x) < 2.
, donc : g(x) < 2.
On a donc montré que g est bornée sur < 2)
2. f est une fonction linéaire, on a : = +\infty \text{ et } \displaystyle \lim_{x \to -\infty} f(x) = -\infty) .
.
f ne peut donc pas être bornée sur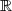 .
.
3. Pour tout réel x,
 = g(3x - 5) = \dfrac{2(3x - 5)^2 + 1}{(3x - 5)^2 + 1}) .
.
Comme g est bornée sur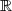 et que f est bien définie sur
et que f est bien définie sur 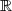 , alors
, alors 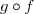 est bornée sur
est bornée sur 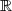 .
.
4. Pour tout réel x,
 = f\left(\dfrac{2x^2 + 1}{x^2 + 1}\right)\\ \hspace{10pt} = 3 \times \dfrac{2x^2 + 1}{x^2 + 1} - 5\\ \hspace{10pt} = \dfrac{6x^2 + 3 - 5x^2 - 5}{x^2 + 1}\\ \hspace{10pt} = \dfrac{x^2^ - 2}{x^2 + 1})
Même raisonnement qu'au 1. :
Pour tout réel x, = \dfrac{x^2 + 1 - 3}{x^2 + 1} = 1 - \dfrac{3}{x^2 + 1}) .
.
Donc : pour tout réel x, < 1)
 = \dfrac{x^2 + 1 - 3}{x^2 + 1} = \dfrac{3x^2 - 2x^2 + 1 - 3}{x^2 + 1} = \dfrac{3x^2 - 2x^2 - 2}{x^2 + 1} = \dfrac{3x^2 - 2(x^2 + 1)}{x^2 + 1} = -2 + \dfrac{3x^2}{x^2 + 1}) .
.
Donc : pour tout réel \geq -2)
D'où :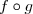 est bornée
est bornée 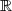 .Publié par Tom_Pascal
le
.Publié par Tom_Pascal
le
Fonctions bornées
Dans chacun des exercices 1 à 6, f désigne une fonction définie sur l'intervalle I.
Montrer que f est bornée sur I.
exercice 1
I = [-3; 2] et f(x) = |x - 3|exercice 2
I = [-4; 1] et f(x) = x²exercice 3
I = [-2; 2] et f(x) = x² - 1exercice 4
I = [-1; 2] et f(x) = |2 - x²|exercice 5
I = [-1; 3] et f(x) = x² - 2xexercice 6
I = [0; 3] etexercice 7
On considère les fonctions1. a) Montrer que pour tout nombre réel
b) Montrer que pour tout nombre réel
c) En déduire que pour tout nombre réel
2. La fonction
3. Démontrer que la fonction
4. Démontrer que la fonction
exercice 1
f(x) = |x - 3|; I = [-3; 2]Si x
D'où : f est bornée sur I.
exercice 2
f(x) = x²; I = [-4; 1]Si x
D'où : f est bornée sur I.
exercice 3
f(x) = x² - 1; I = [-2; 2]si x
Donc f est bornée sur I.
exercice 4
f(x) = |2 - x²|; I = [-1; 2]Si x
Donc f est bornée sur I.
exercice 5
f(x) = x² - 2x; I = [-1; 3]Si x
D'où : f est bornée sur I.
exercice 6
Si x
D'où : f est bornée sur I.
exercice 7
1. a) Pour tout réel x, on a :1. b) Pour tout réel x, on a :
1. c) Pour tout réel x,
Or, pour tout x réel, x² et x² + 1 sont positifs, donc
Pour tout réel x,
Or, pour tout réel x,
On a donc montré que g est bornée sur
2. f est une fonction linéaire, on a :
f ne peut donc pas être bornée sur
3. Pour tout réel x,
Comme g est bornée sur
4. Pour tout réel x,
Même raisonnement qu'au 1. :
Pour tout réel x,
Donc : pour tout réel x,
Donc : pour tout réel
D'où :
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 Voir l'énoncé seul
Voir l'énoncé seul forum de première
forum de première