Annuler
connectez vous
probabilités en post-bac
- Un best-of d'exos de probabilités (après le bac)
- Équations différentielles : un Cours complet avec des exemples
- Ensemble et application Partie II
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Ensemble et application Partie I
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... École ingénieur ProbabilitésTopics traitant de probabilités [tout]Lister tous les topics de mathématiques
Niveau école ingénieur
A propos de la loi uniforme.
Posté par Pax
Yop to all,
J'ai un exo à préparer pour mes partiels sur la loi uniforme. J'ai fait mon exo, mais la fin me laisse plus que sceptique. Est-ce qu'il serait possible d'avoir des retours de gens qui s'y connaissent mieux que moi svp ?
Voilà l'énoncé :
Citation :
a. Soit Y une va de loi uniforme U([0,1]) et a un réel strictement négatif. Déterminer la loi de la va aY.
b. Soient X et Y deux va indépendantes de même loi uniforme U([0,1]). Déduire de la question précédente la loi de X-Y (on pourra s'aider de la convolution). Retrouver, à l'aide de sa densité, mais sans aucun calcul, l'espérance de X-Y.
a. Soit Y une va de loi uniforme U([0,1]) et a un réel strictement négatif. Déterminer la loi de la va aY.
b. Soient X et Y deux va indépendantes de même loi uniforme U([0,1]). Déduire de la question précédente la loi de X-Y (on pourra s'aider de la convolution). Retrouver, à l'aide de sa densité, mais sans aucun calcul, l'espérance de X-Y.
Alors, pour la question a. je suis passé par une fonction PHI, et j'en ai déduis que Z=aY avait pour densité (1/a)*Indicatrice de z sur [a,0]
Pour la question b. j'ai utilisé ce résultat, donc la va -Y suit une loi de densité -1*Indicatrice de y sur [-1;0].Je suis passé par une convolution pour parvenir au résultat que je mets en image, mais ça me parait complètement faux. Je pense que le souci vient du passage aux bornes de l'intégrale via les indicatrices, mais j'en suis pas certain..
Merci d'avances à ceux qui accepteront de se pencher sur mon cas
Loïc
Ps. Sur mon papier, à la toute première ligne, j'ai inversé les bornes de mon indicatrice, c'est évidemment une erreur!
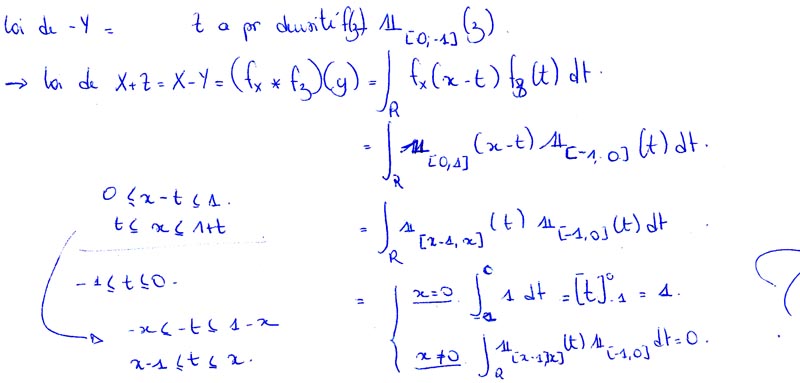
Bonsoir,
pour la question a. il faut faire attention au signe : c'est
pour la b. il est évident (géométriquement) que la densité de X-Y est :
elle est proportionnelle à la longueur du segment de la droite et du carré
Bonsoir,
Merci pour la réponse.
Par contre, je ne comprends pas pourquoi la densité sera avec un signe négatif devant. Pour moi, on a :
z = ax d'où dz = adx donc dx=(1/a)dz.
Donc quand je fais mon changement de variable dans l'intégrale, je peux sortir le (1/a). Ce qui ne me dit pas d'où vient le signe moins d'ailleurs. Si vous pouviez m'expliquer.. 
Et merci beaucoup pour la réponse à la question b.
Citation :
z = ax d'où dz = adx donc dx=(1/a)dz.
Donc quand je fais mon changement de variable dans l'intégrale, je peux sortir le (1/a). Ce qui ne me dit pas d'où vient le signe moins d'ailleurs. Si vous pouviez m'expliquer..
z = ax d'où dz = adx donc dx=(1/a)dz.
Donc quand je fais mon changement de variable dans l'intégrale, je peux sortir le (1/a). Ce qui ne me dit pas d'où vient le signe moins d'ailleurs. Si vous pouviez m'expliquer..
mais l'intégrale est de 0 à a comme a est négatif on la transforme en intégrale de a à 0 pour avoir l'indicatrice, d'où le signe -
Par ailleurs il est bon de savoir qu'une densité de probabilité est toujours positive (au sens large).