Inscription / Connexion Nouveau Sujet
Aire sous une courbe
Bonjour,
voici l'énoncé d'un exercice que je ne comprends pas du tout. J'aurais besoin de quelques pistes.
On appelle aire sous la courbe Cf, d'une fonction f sur un intervalle [a;b], l'aire délimitée par , les droites d'équations
,
et l'axe des abscisses.
On donne la fonction définie par
sur [0,5 ; 2]
On désire faire une approximation de l'aire sur [1;x] avec
. Pour ce faire on va utiliser une méthode (dite des rectangles) utilisant la somme des aires des rectangles ayant pour hauteur
et largeur
avec
et
,
On notera la somme des aires des rectangles définis ci-dessus, x et n étant fixés.
1) tracer la courbe Cg et les rectangles pour x=1,1 et n=5. Calculer A(1,1 ; 5)
2) Donner une expression simplifiée de .
3) Calculer les pour
{2;3}
Je ne sais pas du tout par où commencer. Merci de votre aide! Il me semble que c'est en rapport avec les intégrales, chapitre que je n'ai pas encore vu.
Toujours personne?
Il me semble que A représente l'aire du rectangle A(1,1 : 5) Mais je ne vois pas comment la calculer
J'ai bien la largeur qui est égal à donc je suppose qu'avec les données ça fait
donc
Mais que faire de ce résultat?
Je cherche a placer mes rectangles deja. Je sais que je dois diviser l'intervalle en 5 parties mais je ne comprends ce que viens faire le x=1,1 la dedans.!
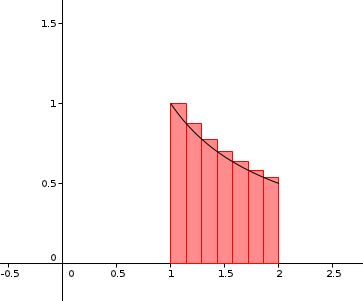
voilà l'aire que tu veux approcher

tu l'approches par des rectangles placés sous la courbe : ce sera une valeur inférieure à l'aire cherchée

tu l'approches par des rectangles placés au-dessus de la courbe : ce sera une valeur supérieure à l'aire cherchée
Ok mais je dois bien diviser en 5 rectangles n'est-ce pas? Et ce sur l'intervalle [0.5;2]
Mais je ne suis pas sûr de ce que le x vient faire la dedans.
Et puis pour calculer l'aire de A que faut-il faire?
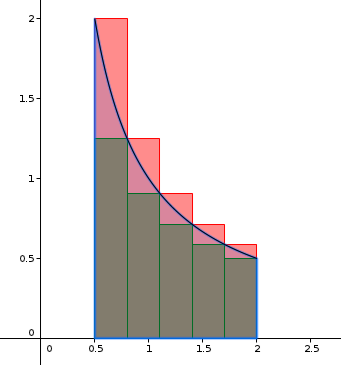
effectivement, c'était sur l'intervalle [1/2;2] et pas [1;2]
j'ai divisé en 7 pour illustrer la situation
et pour calculer l'aire des rectangles verts, tu fais la somme des aires de chaque rectangle vert.
allo, houston, ici apollo 13, je crois qu'on a un problème.
Mais justement je ne vois pas du tout comment calculer l'aire de ces rectangles, je n'ai jamais calculer d'aires dans un repère!
J'imagine qu'il faut utiliser les formules données dans l'énoncé mais je ne sais absolument pas comment.
Je sais bien qu'il y a un problème...


