Inscription / Connexion Nouveau Sujet
Algo des differences divisées (Newton)
Bonsoir à tous, voici l'énoncé de mon exercice (je souhaiterai vérifié que ce que j'ai fait est bon, sachant que j'ai qlq probleme de comprehension)
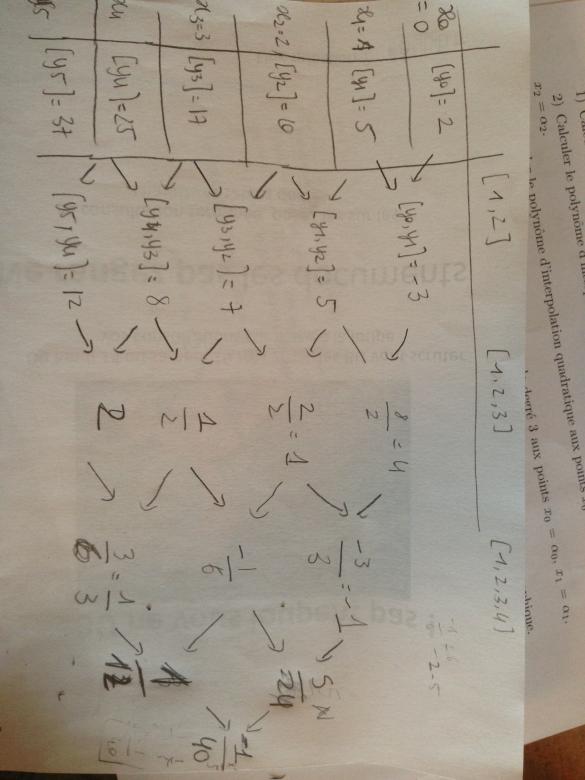
Étant donnés les points xi = i, pour i= 0,1, ..., 5 et les valeurs y0= 2, y1 = 5 , y2= 10, y3 = 17, y4= 25 et y5= 37, calculer à l'aide de l'algorithme de Newton, pour n = 0,1..., 5 le polynome Pn qui interpole les valeurs y0, ... yn aux points x0,...xn
Voilà les valeurs que j'obtiens en faisant mon algorithme de Newton (1ere image)
Sachant que Pn est donné dans l'enoncé :
J'obtiens :
Merci d'avance


 analyse en post-bac
analyse en post-bac