- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
algorithme
salut
svp comment on ecrit un algo qui donne la racine carre d'un nombre?
MERCI D'AVANCE
Par exemple avec Algobox.
Dichotomie (avec précision demandée)
VARIABLES
x EST_DU_TYPE NOMBRE
haut EST_DU_TYPE NOMBRE
bas EST_DU_TYPE NOMBRE
milieu EST_DU_TYPE NOMBRE
precision EST_DU_TYPE NOMBRE
compteur EST_DU_TYPE NOMBRE
DEBUT_ALGORITHME
LIRE x
LIRE precision
haut PREND_LA_VALEUR x
bas PREND_LA_VALEUR 0
compteur PREND_LA_VALEUR 0
milieu PREND_LA_VALEUR x/2
TANT_QUE (compteur < 10000 ET abs(milieu * milieu - x) > precision) FAIRE
DEBUT_TANT_QUE
compteur PREND_LA_VALEUR compteur+1
milieu PREND_LA_VALEUR (haut + bas)/2
SI (milieu * milieu > x) ALORS
DEBUT_SI
haut PREND_LA_VALEUR milieu
FIN_SI
SINON
DEBUT_SINON
bas PREND_LA_VALEUR milieu
FIN_SINON
FIN_TANT_QUE
AFFICHER "La racine carrée est :"
AFFICHER* milieu
AFFICHER "A moins de :"
AFFICHERCALCUL (haut-bas)
FIN_ALGORITHMESauf distraction - A vérifier

Bonsoir !
la réponse de jarod128 te propose une suite définie par récurrence.
Si tu cherches un algorithme de calcul des décimales d'une racine carrée, voir ici ![]() Developpement decimal
Developpement decimal
post du 06-06-15 à 16:24
C'est un algorithme très simple et très rapide. plus rapide que la dichotomie.
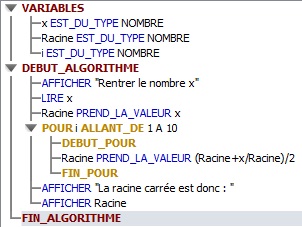
J'ai mis en boucle pour i=1 à 10, mais normalement 3 ou 4 suffit.
Bien entendu ceci dépends de la précision recherchée. On peut aussi utiliser la boucle TANT QUE
Merci a vous pour vos apports..
Stp Razes pour ton algo peux tu m'expliquer on met en boucle i de 1 a quelle valeur selon la precision cherchee?
Il ne faut en tous cas pas limiter à 10 le nombre de boucles dans l'algo proposé par Razes.
L'erreur peut sinon être très grande, par exemple avec x = 123456789
La racine donnée après 10 boucles est 120904,41 alors que la racine correcte est : 11111,11106...
Donc après 10 boucles, dans un tel cas, erreur d'environ 1000 %.
Il est préférable de remplacer la boucle "Pour i allant de 1 à 10"par une boucle "tant que" dans laquelle on teste si la réponse est "bonne" à une erreur près (qui a du être entrée au départ).
(similaire à cette de l'algo que j'ai donné avec la méthode dichotomique)
Et si on veut tenir compte des propriétés de algobox, bloquer par un compteur le nombre de boucles max possibles (pour ne pas planter algobox si la précision n'est jamais atteinte)...

Merci a vous pour vos apports..
Stp Razes pour ton algo peux tu m'expliquer on met en boucle i de 1 a quelle valeur selon la precision cherchee?
L'exemple de 10 boucles était à titre indicatif et comme je l'avais précisé dans ma réponse:
C'est un algorithme très simple et très rapide. plus rapide que la dichotomie.
J'ai mis en boucle pour i=1 à 10, mais normalement 3 ou 4 suffit.
Bien entendu ceci dépends de la précision recherchée. On peut aussi utiliser la boucle TANT QUE
Ceci dépendrait de la précision recherchée.
Par ailleurs, je t'ai indiqué aussi qu'on pouvait utiliser la boucle TANT QUE qui te permettra de comparer deux valeurs successives trouvé et décider à quelle conditions arrêter la boucle: Par exemple soient
a)
ou
b)
Bien entendu, ce n'est pas limitatif et ceci dépends de ta stratégie, du temps de calcul, capacité de la machine, ...



 autre en post-bac
autre en post-bac