Inscription / Connexion Nouveau Sujet
analyse
Je n'ai pas réussi à établir l'inégalité j'ai utilisé les identité remarquable de (a+b)³ même l'inégalité de la moyenne arithmético géométrique a +b ≥ √(a.b) mais je n'ai pas réussi n'ont plus est ce que quelqu'un pourrait y jeter un coup d'œil
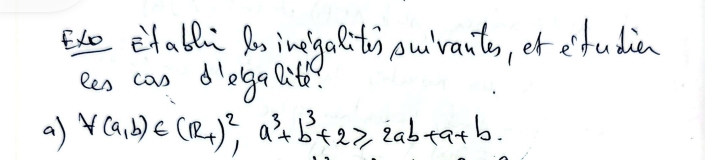
Bonjour,
Une manière parmi d'autres :
Déterminer les extrema d'une fonction à 2 variables (si cela a été enseigné)
f(a,b) = a³+b³+2-2ab-a-b
point critique pour a = b = 1 (en se limitant à R+²)
A > 0 et AC-B² > 0
--> f est minimum pour a = b = 1
(a³+b³+2-2ab-a-b)min = 1+1+2-2-1-1
(a³+b³+2-2ab-a-b)min = 0
--> a³+b³+2-2ab-a-b >= 0
a³+b³+2 >= 2ab + a + b
Le"=" pour a = b = 1
Bonsoir 
Une idée possible :
En posant et
l'inégalité demandée s'écrit
ou encore
ce qui est vérifié vu que
sauf erreur bien entendu
Bonjour,
En ramenant tout à gauche et en cherchant à factoriser on voit que l'inégalité demandée est équivalente à montrer que :
Ce qui est toujours vrai lorsque a≥-1 et b≥-1
Annuler
connectez vous
analyse en post-bac