Inscription / Connexion Nouveau Sujet
Ancienne question sur une section d'un tétraèdre
Bonjour,
en ce moment, comme, je ne suis pas super bon sur les sections, je m'entraîne sur plein de sections que je trouve sur Internet, mais certaines sont évidentes et d'autres difficiles.
Et là, il y a quelques jours, je suis tombé sur une section demandé par un ancien élève sur votre site dont voilà le lien: https://www.ilemaths.net/sujet-section-pyramide-517254.html qui n'est pas terminé. Et j'ai une piste lorsque le modérateur demande l'intersection de EFG à SAD :il y a déjà le point E comme intersection mais est-ce que la droite parallèle à AD passant par E, est une intersection de EFG à SAD ? Si vous pourriez me montrer sous formé de schéma, si je comprends pas de temps en temps et puis après la section finale, ça serait bien 
Merci d'avance et au revoir.
![]() Section pyramide
Section pyramide
Voilà le lien en url, comme ça sera plus pratique pour vous.
Bonjour,
prendre comme base une discussion qui comporte autant d'erreurs au départ n'est peut être pas un bon plan !!!
qu'en penses tu, toi ?
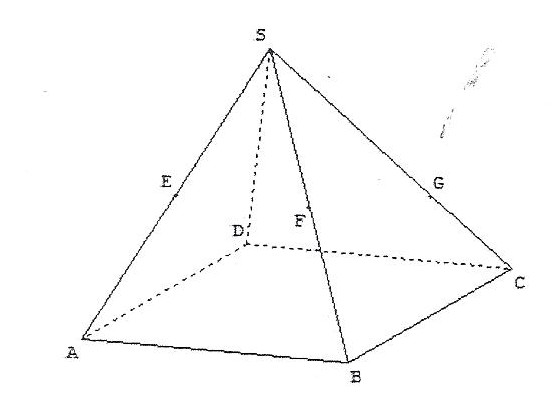
le principe de base relève de la simple évidence à partir d'une représentation mentale de l'objet véritable dans l'espace :
quels sont les plans, les droites etc
qu'est ce qui est dans ce plan et qu'est ce qui n'y est pas etc
ainsi si on s'intéresse à la droite (EF) il est évident (si la représentation mentale qu'on a de cet objet est correcte) qu'elle est contenue dans le plan (SAB)
et que les seules autres droites connues de la figure qui sont dans ce plan sont les droites (SA), (SB) (sans intérêt pour la question) et (AB)
donc ce seront les seules droites connues susceptibles de couper la droite (EF)
rappelons qu'une droite est illimitée et que un plan aussi
ne pas confondre le plan (SAB) et la face SAB, ni la droite (AB) et le segment [AB]
la suite est en fait assez évidente si on comprend ce principe de base et si la représentation mentale de l'objet est correcte.
si on a du mal à se représenter un objet à partir d'une image de cet objet, on peut en faire un en pâte à modeler ... 
c'est surtout une question d'habitude.
il faut parfois y ajouter quelques "théorèmes" sur les droites et plans parallèles ou orthogonales
sur les théorèmes bien connus de géométrie plane (qu'on applique dans un des plans de l'espace) comme Thalès, Pythagore etc
Bonjour,
Il vaut mieux rester à l'intérieur de la pyramide SABC
Si H est le centre de La base ABCD, les droites EG et SH se coupent en un point J dans le plan EFG
La droite FJ coupe SD au point cherché dans le plan EFG
PS:
quant à la rédaction formelle en détail plus ou moins ... détaillés
on pourrait par exemple dire :
E est dans la droite (SA) qui est contenue dans le plan (SAB)
F est dans la droite (SB) qui est dans le plan (SAB)
donc E et F sont dans ce plan
et par conséquent la droite (EF) est dans ce plan etc ...
ou se contenter de dire (EF) est dans le plan (SAB) (parce que c'est suffisamment évident !!)
tout dépend des questions de l'énoncé
et puis il n'y a pas qu'une seule façon de faire la construction.
d'accord que la tienne est plus expéditive.
qu'en penses tu, toi ?
on ne va pas te le faire à ta place
surtout que en fait vham a fait 99.9% du boulot !!
(relire ce qu'il a dit et chercher à le comprendre)
il est impossible de "comprendre à ta place" , ça ne rime à rien
nous on sait faire
c'est à toi et uniquement à toi de chercher à comprendre ce qu'on te dit.
J'ai vu ce qu'il a fait ce que je comprends pas C'est lorsqu'il dit FJ coupe SD, en regardant la figure je n'arrive pas à voir que FJ coupe SD désolé j ai un peu du mal avec la géométrie dans l espace 
TOUT est exclusivement sur la notion de quels plans, quelles droites sont dans quel plan ou pas, quels points sont dans quelle droite ou dans quel plan ou pas etc
c'est uniquement ça
"en regardant la figure" : évidemment puisque ces droites ne sont pas tracées et qu'il n'y a rien à "voir"...
Il faut (c'est à dire que c'est indispensable et qu'il n'y aucun autre moyen) juste une bonne dose d'imagination pour voir
une représentation mentale de l'objet véritable dans l'espace :
après on formalise par du raisonnement du genre de ce que je disais :
tel point est sur telle droite qui fait partie de tel plan donc est dans ce plan etc
F est dans le plan (SBD) (évident)
J est dans ce même plan parce que on l'a construit ainsi (intersection des droites (SH) et etc et (SH) est dans le plan (SBD) )
donc (FJ) est dans ce plan (SBD)
(SD) est dans le plan (SBD) (évident)
les deux droites (SD) et (FJ) qui sont dans dans un même plan ((SBD)) se coupent ou sont parallèles
ici elles ne sont "évidemment" pas parallèles
(on peut le prouver formellement mais est-ce nécessaire ?)
donc elles se coupent en un point K etc
(les tracer effectivement sur le dessin permet donc de construire ce point K !)
bien sur que non
pourquoi donc y serait-il ?
ça n'intervient d'ailleurs nulle part dans le raisonnement.
on parle du plan (SAC) et (SBD) pour faire intervenir leur intersection (SH)
et dans (SAC) de la droite (EG) pour définir J
puis dans (SBD) de la droite (FJ) pour définir K sur la droite (AD)
au final on va devoir justifier maintenant (une fois tout ça tracé effectivement, on n'en voit aucune trace ici de tes tracés !!) pourquoi ce point K est dans le plan (EFG)
et ainsi terminer la section de la pyramide par ce plan (EFG)
parce que elles sont toutes deux dans le même plan (SAC)
et elles ne sont "évidemment" pas parallèles
une idée : tu sembles avoir des difficultés insurmontables à voir ce dessin comme une véritable pyramide réelle dans l'espace
alors fais en une !!
tu as bien vu en collège comment faire une pyramide avec un patron de pyramide
et tu écris dessus les points E, F, G, H etc
tu peux "ouvrir" ta pyramide pour matérialiser avec des feuilles de bristol supplémentaires les plans dont on parle (SAC), (SBD)
cadeau :
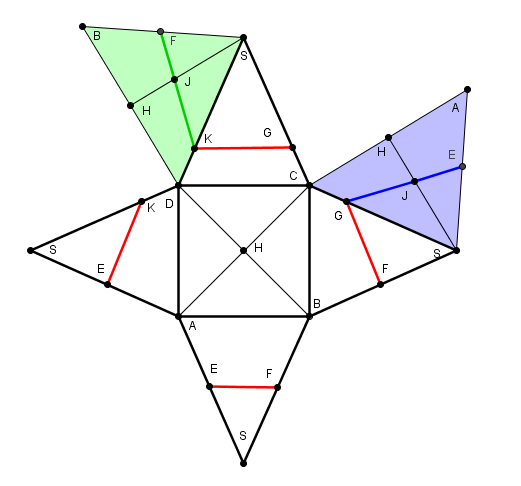
imprimer et découper ce patron de la pyramide, repasser les noms de points et traits sur le verso de la feuille
les morceaux supplémentaires en vert et bleu sont les plans (SAC) en bleu et (SBD) en vert, à replier à l'intérieur de la pyramide
bien sûr que non
K, il est dans (SBD)
la droite (FJ) qui sert à définir K est dans (SBD) (F est dans SBD)
l'exercice entièrement résolu
et basta (pffffff cr.. irrécupérable)
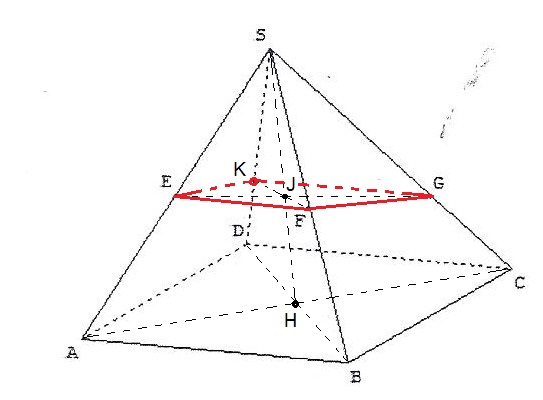
Bonne nuit,
Pour s'habituer à bien voir les intersections de droites dans les différents plans :
La méthode utilisant le point H intersection de [AC] et [BD]donne le point K sur [SD] et [FJ]
La méthode utilisant le point P intersection de (BC) et (FG)donne le même point K
intersection de [SD] et [FQ] en ayant Q intersection de (BD) et de la parrallèle à (AB) menée par P
On remarque aussi que l'intersection R de (AC) et (EG) est alignée sur la droite (PQ) parallèle à (AB)

Merci à vous 2 mais la section lorsque J'ai les points d intersections et quelles intersections, j'y arrive mais C'est juste à trouver les points que J'ai du mal. 
Vham ce que vous avez fait c est assez complexe mais je vais m'y habituer avant le contrôle et le Bac.
parce que pour toi cette figure représente un dessin plan à plat sur la feuille et rien d'autre et que tu n'arrives pas à croire que cela est la vue d'un véritable solide dans l'espace...
et donc à voir réellement les plans dont on parle dans le texte.
et puis je suis persuadé que en fait tu n'as même pas tracé les droites dont on te parlait au moment où on t'en parlait et que ces éléments restaient donc totalement abstraits et uniquement en parlotes
des droites dont on connait deux points, c'est pourtant facile à tracer !!
pour t'entrainer une variante un peu plus compliquée (quoique..) où les points E,F,G donnés ne sont pas sur les arêtes de la pyramide mais sur les faces :
E sur SAB, F sur SBC et G sur SCD
ici c'est un cas "simple" où le plan (EFG) n'est pas tellement incliné et coupe effectivement les arêtes [SA], [SB], [SC], [SD] de la pyramide

là aussi on utilise deux plans auxiliaires (SEG) et (SAF) qui jouent exactement le même rôle que les plans (SAC) et (SBD) du 1er problème
essaie de comprendre cette construction (il s'agit de construire le point M d'intersection du plan (EFG) avec l'arête (SA) de la pyramide, terminer la section est alors un jeu d'enfant)
Bonjour,
Salut et Bravo mathafou pour ce dernier exemple
>> PTApanage : dites-nous, sur ce dernier dessin "dans l'espace" de mathafou dans quel ordre vous détermineriez les points en partant de E, F, G sur les faces de la pyramide SABCD.
Si vous les donnez correctement nous saurons que nous n'avons pas perdu notre temps....
Je crois avoir compris en faite je dois vous dire les intersections des telles droites avec telles droites pour arriver à la fin de la section d après le dessin de mathafou?
Merci mais auriez-vous des petits exercices comme ça pour que je puisse m'entraîner sur les sections ? Qui seraient adapté à mon niveau? Merci d avance et bonne après midi.
alors, ne me demandez pas comment je viens d'arriver sur cette page...je ne l'avais jamais vue !
![]() [lien]
[lien]
PTApanage, descends dans la page, tu as les sujets où on parle de sections planes
J'ai jamais fait vos sections planes en spécialité mathématiques, J'ai fait que des sections de cube et de tétraèdre en maths normal.
peu importe ...que ce soit en spé maths ou dans un autre cours;..faut pas compartimenter comme ça !
mais tout ce que tu as fait jusqu'à présent sont des sections de "je sais pas quoi" par des plans...c'est donc ce qu'on appelle une section plane !
pour tenter dans trouver d'autres, tu vas sur cette page ![]() [lien]
[lien]
tu choisis seconde, ou 1re ou terminale puis géométrie dans l'espace à chaque fois, mais il va falloir fouiller !
ou bien, à l'aide de la fonction "recherche" en haut à gauche




