Inscription / Connexion Nouveau Sujet
Approximation d une fonction à l ordre 2
Bonjour tout le monde .
Je dois donner l approximation a l ordre 2 de x sin(2x) si x = pi/4
J ai dérivé une première fois ce qui me donne : sin(2x) +2x cos(2x)
J ai dérivé encore une fois ma réponse précédente : 4cos(2x)-4x sin(2x) OK ca va pour faire cela. Après je dois utiliser la formule y= f(x0)+ (x-x0) f'(x) + [(x-x0)^2]/2!
Mon souci est la valeur de x0. Je choisis? Je fais quoi ?
Si quelqu un peut le résoudre ce serait vraiment bien
Merci d'avance
Quand je calcule pour l ordre 1 quand x0=0 je tombe plus au moins a la valeur de xsin(2x) quand x vaut pi/4. Mais c est que j ajoute pour être a l ordre 2 quand je m éloigne vraiment. Me serais je trompée dans le dérivée seconde ?
Bonjour,
Je dirais qu'il faut choisir x0=
/4 ... 
Les calculs sont justes pour les dérivées première et seconde et j'obtiens le DL suivant :
f(x)
=2/32+(1-/4)x+x2/2 au voisinage de /4
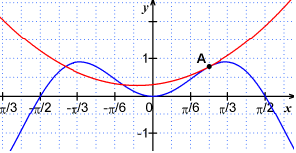
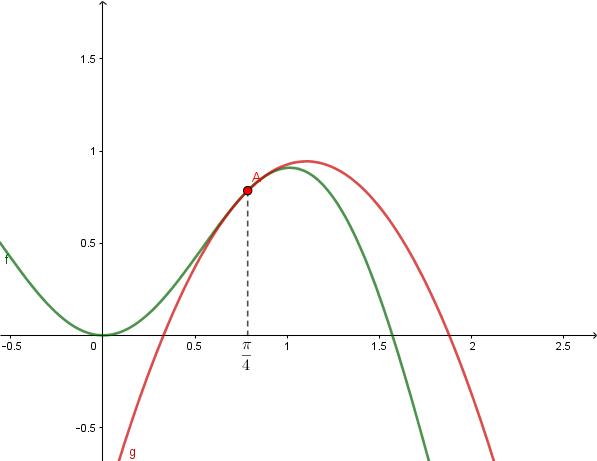
La représentation graphique confirme bien cette approximation .
Le "x", tu le laisses tel quel: ta formule te donne une approximation (à l'ordre 2) de f(x) pour x proche de /4.
C'est aussi une fonction de x (un polynôme du second degré)
Annuler
connectez vous