Inscription / Connexion Nouveau Sujet
Approximation de racine(17) avec une précision 10^-2.
Bonsoir,
Je voudrais en utilisant les développements limités, calculer une approximation de avec une précision de 10-2.
Je sais qu'il faut utiliser les développements limités, car j'ai déjà traiter des exemples "similaires" dans mon cours. Je sais également que la condition de précision, joue sur le reste du développement limité. "Reste" qu'on nomme, "reste de Lagrange".
Mon problème est pour démarrer, car je ne sais pas si écrire le développement limité de par exemple : (d'après
), est la bonne piste/judicieux.
Merci d'avance pour vos conseils.
Si tu prends x=16, penses-tu que les qui interviendront dans le développement de Taylor tendront vers 0 quand n tend vers l'infini ?
Ah (?)
Je peux poser : et faire le développement limité de cette fonction. Enfin, c'est surtout le reste qui m'intéresse. Si je ne dis pas de bêtises, je fais essayer comme ça.
Merci bien pour la remarque  .
.
Oui, je me suis rendu compte qu'en faite le 16 n'a pas vraiment "d'importance" au sens mathématique.
J'essaie de résoudre ça, et je te tiens au courant.
Merci en tout cas  .
.
Ok alors je me lance (pas sûr à 100%) :
J'exprime le reste de Lagrange comme ceci pour ma fonction f(x) :
Je peux dire que je travaille pour x compris entre 0 et 1 (?), et c appartient donc à l'intervalle [0,1].
Alors au numérateur on a la dérivée (n+1)ième de f(x) qui apparaît, si je me fie au développement limité de , je peux considérer que :
(?) (Je ne suis pas sûr du tout de ce passage là..)
Du coup mon expression s'écrit :
Et selon mes conditions de départ, cela doit être inférieure ou égal à 10-2.
Etant donné que je travaille sur [0,1], je peux majorer mon expression par ceci :
, et ceci est inférieure ou égal à 10-2 pour n=4 (calculatrice).
Du coup ma réponse finale serait (en prenant x=1) :
 4 + 1/2 - 12/3 + 13/16 - 5.14/128
4 + 1/2 - 12/3 + 13/16 - 5.14/128  4.19.
4.19.
Qu'en pensez-vous ?
Merci d'avance  .
.
Salut Earthquake48
Soit un nombre quelconque strictement positif
Connais tu ?
la suite récurrente qui est définie par la relation de récurrence
avec quelconque
Cette suite converge vers le nombre
et un exercice de type BAC bien connu consiste à chercher le rang tel que
(par exemple)
Cette suite (de Héron) permet de calculer / d'approcher la valeur décimale du nombre irrationnel
ps)
dans cet exo pour calculer une valeur approchée de :
il suffit de poser
et de calculer le rang tel que
soit une valeur approchée de
au centième près (à
près)
Bonsoir ptinoir_phiphi  ,
,
Oui j'ai déjà entendu parler de la suite de Héron, et ton explication est très claire, seulement pour cet exercice en particulier, je n'ai pas le droit d'utiliser ça, je dois faire ça uniquement avec les développements limités (ce que j'ai essayé de faire..).
Merci pour ta réponse.
Bonjour GaBuZoMeu,
En effet, je n'avais pas tout à fait saisi le sens de ton indication.. Je refais ça.
Merci bien  .
.
Au fait : la formule que donne ptitnoir_phiphi pour la suite de Héron est complètement farfelue. Un conseil : relis-toi et tourne sept fois la souris sur le tapis avant de balancer tes messages !
Une incertitude persiste, à ce niveau là :
, je ne pense pas vraiment pouvoir écrire ça, car la dérivée (n+1)ième de
, n'est pas
.. Seulement je n'ai pas trouvé d'autres moyens de l'exprimer.
Du coup je retombe toujours sur un n valant 4, or d'après la calculatrice ce serait plutôt aux alentours de 2-3 qu'il faudrait s'arrêter pour avoir la bonne précision il me semble.
Comment corriger cette erreur ?
Merci d'avance.
Oh la la ! Relis toi, "la dérivée (n+1)ième de " est une énormité !
A part ça, l'expression des dérivées successives de où
est un réel non entier naturel, ce n'est pas si affreux que ça.
Bonjour
il te faut trouver un majorant M de la dérivée n+1 ième de racine(1+x) sur ]0; 1/16[, et ton erreur sera inférieure à
relis ce que tu as écris : la dérivée n+1 ième d'une constante, ça vaut zéro, je ne pense pas que ce soit ce que tu voulais faire.....
Pardon, bien sûr je voulais écrire x !.. (Dommage qu'on ne puisse pas éditer les messages après coup sur l'île  ).
).
Non ce n'est pas si affreux, mais quand même.. Ca donnerait quelque chose comme ça si je ne me trompe pas :
Du coup au lieu d'écrire cn+1, peut-être puis-je écrire : 1/2*cn+1 ? Sinon, je ne vois pas comment obtenir quelque chose de plus précis que n=4..
Qu'as-tu écrit ? "Ca donnerait", c'est quoi ? Si tu faisais l'effort d'être plus précis, sans doute y verrais-tu plus clair. La précision, ça coûte au départ, mais ça paie largement à l'arrivée.
Qu'entends-tu par précision ?! Mon expression est suffisamment précise je trouve, je peux encore développer un peu plus :
1/2(-1/2)(1/2-3)(1/2-4).. : en gros, un nombre négatif quoi qu'il arrive.
Je trouve déjà une réponse, à savoir n=4, j'obtiens bien sûr une approximation à 10-2 comme demandé, seulement au vue du résultat que je trouve à la calculatrice, elle n'est pas assez "exacte".
Si je majore par 1/2*cn+1, ce sera encore plus exact théoriquement, mais ma question était de savoir par quoi majorer justement.
Je passe sans doute à côté de quelque chose..(Désolé). 
Pour qui serait déçu par cette fin en queue de poisson :
Si on écrit Taylor-Lagrange à l'ordre 1, on a qu'il existe entre 0 et 1/16 tel que :
La valeur absolue de l'erreur faite en oubliant le reste peut donc être majorée par .
Donc
L'estimation de l'erreur (de l'ordre de 2/1000) faite ci-dessus est bien précise :
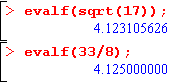
On peut remarquer que 33/8 est aussi la valeur obtenue après la première étape de la méthode de Héron partant de 4 (la vraie méthode de Héron, celle donnée par pour calculer la racine carrée de
).



 analyse en post-bac
analyse en post-bac