Inscription / Connexion Nouveau Sujet
Approximation du nombre pi méthode d'Archimède
Bonsoir j'espère que vous allez bien j'ai besoin d'aide pour cette exercice niveau terminale.
On considère un cercle C de diamètre 1. Archimède constate qu'il est possible de construire des polygones réguliers inscrits et circonscrits à C. Plus précisément, si n est un entier naturel supérieur ou égal à 3, le cercle C est compris entre deux polygones réguliers à n côtés.
1. Faire une figure pour le cas n = 5
2. Que dire des deux polygones inscrits et circonscrits à C lorsque le nombre n devient grand?
3. Soit un entier naturel supérieur ou égal à 3.
On note U_{n} un polygone régulier à n côtés inscrit dans C et u_{n} son périmètre. De même, on note V_{n} un
polygone régulier à n côtés circonscrit à C et v_{n} son périmètre. En remarquant qu'un polygone régulier à n côtés se découpe naturellement en n triangles isométriques, exprimer u_{n} et v_{n} en fonction de n.
4. (a) Déterminer les valeurs approchées de à 10 ^ - 3 près de u_{100} et v_{100}
(b) Quelle approximation de vient-on d'obtenir?
J'ai fait les deux premières questions je ne suis pas sûr de ma réponse pour la 2 et pour le reste je ne sais pas comment procéder.
Pourriez-vous m'aider s'il vous plaît de m'apporter une réponse.
Bonsoir
Mets ta figure et dis ce que tu as fait pour 2)
 extrait de
extrait de Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?
Prends l'habitude de montrer ce que tu as fait (valable sur cet exercice comme sur les flocons)
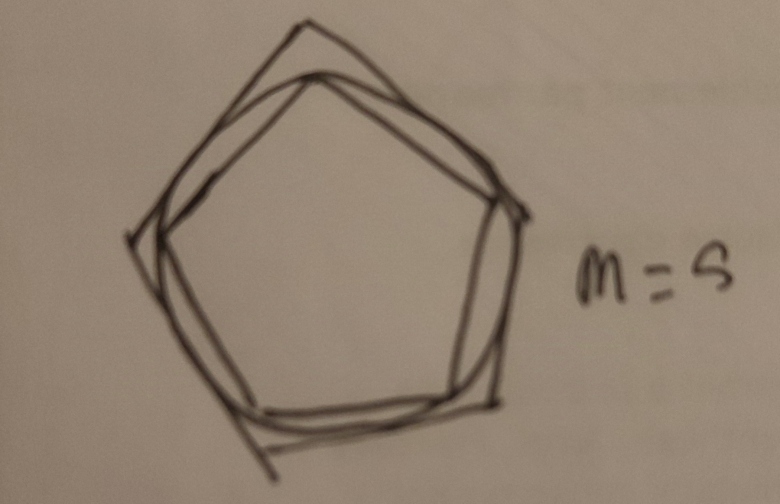
Voici ma figure pour la 1.
Et pour la 2 je n'ai pas vraiment détaillé pour l'instant mais ça tendra vers l'air du cercle et donc ça se reprochera plus du cercl
Bonjour,
Tu n'as pas une règle pour tracer les côtés ?
ça tendra vers l'air du cercle
Es-tu certain que l'on s'intéresse à une aire dans cet exercice ?
Tu peux te contenter de parler de la forme des polygones.
Bonjour,
"pour tracer"... :
et puis pour continuer il sera bon de faire apparaître sur cette figure des noms de points et
...se découpe naturellement...
(c'est surtout pour marquer cette discussion comme digne d'intérêt, je laisse Sylvieg et surtout Ehd poursuivre)
Bonjour,
Il pleut des... cordes !!
Ehd
1) Geogebra (en Terminale tu dois connaitre ?) permet de tracer de belles figures 
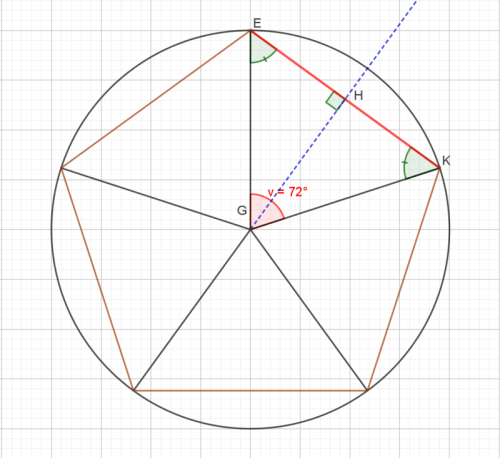
2) Si tu n'arrives pas à traiter le cas général (question 3) essaye au moins d'exploiter le cas particulier où n= 5 (voir la figure). Si tu arrives à calculer le périmètre du... pentagone, dis nous comment tu fais et on t'aidera à.... généraliser 
Bonjour ZEDMAT
??? dans chacun de tes messages la figure est parfaitement visible (et la même, à changement d'échelle près pour la dernière)
Bonsoir Mathafou !!
Voici ce que je vois (à l'instant encore !). Comprenne qui pourra...
L'essentiel est que Ehd puisse voir cette figure et que cela lui donne envie de poursuivre... s'il le veut.
@ mathafou
Effectivement, la combinaison CTRL-F5 a fait apparaitre les figures !!
Je suis admiratif de ton savoir 
Que devient Ehd ?
"Que devient Ehd ?"
toute la question est là ... (pour son autre exo aussi  )
)
du coup on ne peut pas mettre en avant que ... ce n'est pas du tout la méthode d'Archimède qui n'avait à sa disposition que la thie
pour lui donner les fonctions trigo de sans connaitre
à l'avance...
contrairement à l'usage d'une boite magique qui en appuyant sur des boutons donne cette valeur,
... parce qu'elle connait la valeur de et quelques autres constantes dérivées de
, écrites une fois pour toutes dans sa mémoire morte !
(bref l'exo revient à calculer à partir de
!)
Bonjour mathafou,
Voir ![]() Nombre pi et Archimède
Nombre pi et Archimède 


 m'en veut....
m'en veut....