Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Nombres complexesTopics traitant de nombres complexes [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

arythmétique dans la détermination d'un nombre complexe

Posté par
fredisedegnon 07-02-20 à 22:41

bonsoir
le plan complexe est muni d'un repère orthonormé (o,e1,e2). u et v sont deux nombres complexes non nul. déterminer le nombre complexe w= u÷v tel que |u|= 3,  |v| = 5 et |u - v| = 7
proposition de réponse

posons u=a+ib , v=x+iy
|u|=3=> a²+b²=9
|v|=5=> x²+y²=25
|u-v|=7=> (Ax+by)=15/2

u÷v= (Ax+by)÷(x²+y²) +{ (bx-ay)÷(x²+y²) }i
en utilisant les valeurs trouvées ci-dessus la partie réelle donne 15/18 = 5/6
je ne sais plus comment procéder pour trouver la partie imaginaire de w
vos aides me seront très nécessaire. merci

Posté par
lakere : arythmétique dans la détermination d'un nombre complexe 07-02-20 à 22:56

Bonsoir,

Dans certaines circonstances, on peut s'appuyer sur la géométrie.

Pour le module du rapport, pas de problèmes: il vaut \dfrac{3}{5} .

Pour un argument, je vois un parallélogramme, ses diagonales et éventuellement Al Kashi.

Posté par
fredisedegnonre : arythmétique dans la détermination d'un nombre complexe 07-02-20 à 23:16

y

Posté par
fredisedegnonre : arythmétique dans la détermination d'un nombre complexe 07-02-20 à 23:17

<<Pour un argument, je vois un parallélogramme, ses diagonales et éventuellement Al Kashi.>>

je ne comprends pas ce que vous voulez m'expliquer par cette phrase

Posté par
fredisedegnonre : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 00:04

aider moi s'il vous plaît

Posté par
lakere : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 00:09

Essaie de faire un dessin:

Dans le repère orthonormé O,\vec{e_1},\vec{e_2}:

Place un point A en sorte que l'affixe de A soit u de module 3

Place un point B en sorte que l'affixe de B soit v de module 5.

\vec{OA}-\vec{OB}=\vec{BA} a pour affixe u-v

Et donc d'après ton énoncé, BA=|u-v|=7

Tu as donc un triangle OAB dont tu connais la mesure des 3 côtés.

De plus, arg\left(\dfrac{u}{v}\right)=(\vec{OB},\vec{OA})\,\,[2\pi] et tu peux calculer le cosinus de cet angle dans le triangle OAB avec par exemple Al Kaschi.

J'ai parlé plus haut de parallélogramme. Là on ne se sert que de la « moitié »

Posté par
fredisedegnonre : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 00:25

s'il vous y donner moi le théorème Al Kaschi.

Posté par
fredisedegnonre : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 00:30

j'ai absolument besoin de votre aide

Posté par
Sylvieg Moderateurre : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 07:46

Bonjour,
Voir VII de Produit scalaire : Rappels, Applications et compléments

Posté par
Sylvieg Moderateurre : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 09:18

@fredisedegnon
Une remarque sur tes calculs :
Avec ax+by =15/2 et x²+y²=25, on ne trouve pas 5/6 comme partie réelle de u/v, mais 3/10.
Une fois 3/10 trouvé, on peut en déduire la partie imaginaire, au signe près, en utilisant le module de u/v qui est connu.

Posté par
Sylvieg Moderateurre : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 09:36

Et on ne peut pas faire mieux

Posté par
Sylvieg Moderateurre : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 09:41

Mais, vu le repère donné au début de l'énoncé, c'est plutôt la méthode de lake qui semble attendue.

Posté par
lakere : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 12:08

Une figure:

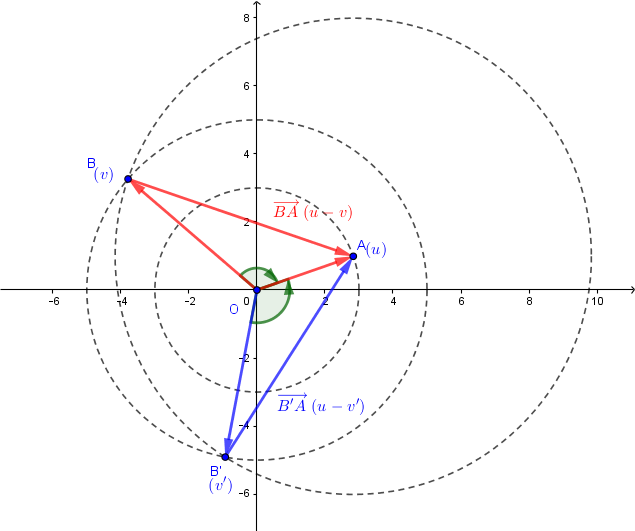
arythmétique dans la détermination d\'un nombre complexe

A est un point quelconque du cercle de centre O et de rayon 3

B et B' sont les intersections du cercle de centre O et de rayon 5 et du cercle de centre A et de rayon 7

D' où deux solutions:

  arg\left(\dfrac{u}{v}\right)=(\overrightarrow{OB},\overrightarrow{OA})\;\;[2\pi]

   arg\left(\dfrac{u}{v'}\right)=(\overrightarrow{OB'},\overrightarrow{OA})\;\;[2\pi]

Cela en sachant que \left|\dfrac{u}{v}\right|=\left|\dfrac{u}{v'}\right|=\dfrac{3}5{}

Une formule:

   \overrightarrow{OA}.\overrightarrow{OB}=OA.OB\,\cos(\overrightarrow{OA},\overrightarrow{OB})=\dfrac{1}{2}(OA^2+OB^2-AB^2)

Posté par
lakere : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 12:25

Une remarque:

  

Citation :
|u-v|=7=> (ax+by)=15/2


Je pense qu'il manque un signe "-"

   et du coup,  \Re\left(\dfrac{u}{v}\right)={\red -}\dfrac{3}{10}
  

Posté par
vhamre : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 15:03

Bonjour,

sur la judicieuse remarque de lake :

Citation :
Tu as donc un triangle OAB dont tu connais la mesure des 3 côtés.

Puisque l'on cherche argument(u/v) = argument(u) - argument(v) autant choisir argument v = 0
u=a+ib   soit a²+b² = 9
v=c+i0   soit c = 5   et (a-c)² + (b-0)² = 49
la troisième équation est   a²-2ac+c²+b² = 49
les valeurs numériques de u sont donc a = ... ; b = ...

Posté par
vhamre : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 15:10

correctif :
En choisissant v=c+i0 on a c = 5, pas simplement c = 5

Posté par
Sylvieg Moderateurre : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 17:33

@lake,
Effectivement, il manquait un moins
@vham,
Oui, c'est tentant de fixer arbitrairement v.
Mais si on ne veut pas avoir à le justifier, on peut démarrer ainsi :
v = 5ei , u = 3ei et d = -.
Ça revient à faire une rotation.
On a alors
u/v = (3/5)eid
et
|v-u| = |5-3eid| = |5-3cos(d)-3isin(d)|

|v-u| = 7 permet de trouver cos(d) puis les deux valeurs possibles de sin(d).

Posté par
lakere : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 17:37

Une méthode calculatoire:

|u-v|=7\Longleftrightarrow (u-v)(\bar{u}-\bar{v})=49\Longleftrightarrow |u|^2+|v|^2-(u\bar{v}+\bar{u}v)=49

  d'où    u\bar{v}+\bar{u}v=-15  (1)

  (u\bar{v}-\bar{u}v)^2=(u\bar{v}+\bar{u}v)^2-4\,u\bar{u}v\bar{v}=(u\bar{v}+\bar{u}v)^2-4\,|u|^2|v|^2

  d'où    (u\bar{v}-\bar{u}v)^2=675=(15i\sqrt{3})^2  (2)

Puis:

   \Re\left(\dfrac{u}{v}\right)=\dfrac{1}{2}\,\left(\dfrac{u}{v}+\dfrac{\bar{u}}{\bar{v}}\right)=\dfrac{1}{2}\,\dfrac{u\bar{v}+\bar{u}v}{|v|^2}=-\dfrac{3}{10} avec (1)

\Im\left(\dfrac{u}{v}\right)=\dfrac{1}{2i}\,\left(\dfrac{u}{v}-\dfrac{\bar{u}}{\bar{v}}\right)=\dfrac{1}{2i}\,\dfrac{u\bar{v}-\bar{u}v}{|v|^2}=\pm\,\dfrac{3\sqrt{3}}{10} avec (2)

Malheureusement, une petite réciproque est nécessaire.

Posté par
lakere : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 17:41

Zut!

Citation :
d'où    (u\bar{v}-\bar{u}v)^2={\red -}675=(15i\sqrt{3})^2   (2)

Posté par
Sylvieg Moderateurre : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 18:27

Deux petites figures pour illustrer quand on part de v :
arythmétique dans la détermination d\'un nombre complexe arythmétique dans la détermination d\'un nombre complexe

Posté par
alb12re : arythmétique dans la détermination d'un nombre complexe 08-02-20 à 18:48

de grâce, que les geometres ne me vouent pas aux gémonies !

Posté par
Sylvieg Moderateurre : arythmétique dans la détermination d'un nombre complexe 09-02-20 à 07:58

Bonjour,
@alb12,
Je lis ceci dans ton lien :
"Le programme renvoyant les 4 valeurs possibles de u/v"
Ensuite il y a 4 expressions, mais égales 2 à 2...
Qu'est-on censé en penser ?

Posté par
lakere : arythmétique dans la détermination d'un nombre complexe 09-02-20 à 09:47

Bonjour Sylvieg

Ah!!! Des dessins!

Tu vas voir: quand on commence, on ne peut plus s'en passer

Posté par
alb12re : arythmétique dans la détermination d'un nombre complexe 09-02-20 à 11:25

Sylvieg @ 09-02-2020 à 07:58

Bonjour,
@alb12,
Je lis ceci dans ton lien :
"Le programme renvoyant les 4 valeurs possibles de u/v"
Ensuite il y a 4 expressions, mais égales 2 à 2...
Qu'est-on censé en penser ?

Le systeme a 4 solutions
(u,v) est solution si et seulement (-u,-v) est solution
donc pour u/v on obtient 2 reponses distinctes

Posté par
Sylvieg Moderateurre : arythmétique dans la détermination d'un nombre complexe 09-02-20 à 14:26

D'accord alb12

@lake,
Je m'y suis mise il y a environ deux ans.
Je poste de temps en temps des dessins ; mais je suis loin de ta virtuosité

Posté par
fredisedegnonre : arythmétique dans la détermination d'un nombre complexe 14-04-20 à 09:39

merci pour votre aide

Posté par
Sylvieg Moderateurre : arythmétique dans la détermination d'un nombre complexe 14-04-20 à 09:56

De rien fredisedegnon
Pas trop dur le confinement ?
Profites-en pour mettre à jour ton profil (tu n'es plus en 1ère).

Posté par
carpediemre : arythmétique dans la détermination d'un nombre complexe 14-04-20 à 13:43

salut

|u| = 3 et |v| = 5 et w = u/v

évidemment u et v ne sont pas nuls et |w| = 3/5

|u - v| = 7 \iff |w - 1| = 7/5

donc le point M d'affixe w appartient aux cercles C(0, 3/5) et C(1, 7/5)

il y a donc deux solutions et par symétrie par rapport à l'axe des réels ces solutions sont conjuguées

il est alors aisé (mais fastidieux) de déterminer explicitement w ... à partir des équations cartésiennes de ces cercles ...

Posté par
Sylvieg Moderateurre : arythmétique dans la détermination d'un nombre complexe 15-04-20 à 08:44

Bonjour,
La méthode qu'avait amorcée fredisedegnon dans son premier message est tout à fait exploitable si on y corrige l'erreur :
ax+by = -15/2.
On en déduit la partie réelle de u/v : -3/10.
Puis les deux parties imaginaires possibles de u/v : (3/10)3.

Ce qui est étonnant, c'est la simplicité des arguments : 2/3.

Le signe d'un cheminement plus simple possible ?


Rechercher
Menu
Espace membre
21 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !