Inscription / Connexion Nouveau Sujet
Associer un graphique à une figure
Bonjour,
J'aimerais savoir si ma méthode de résolution est juste.
Le but est d'associer chaque figure à un graphique.
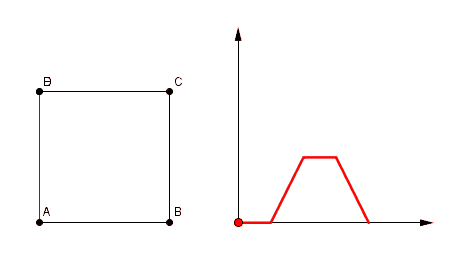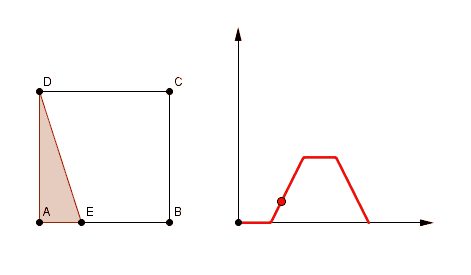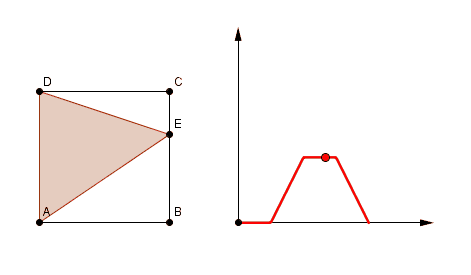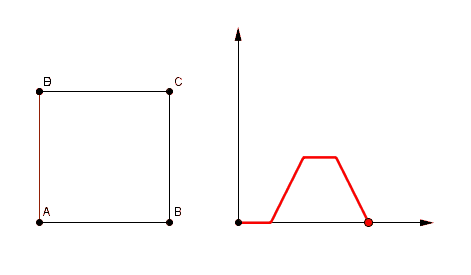
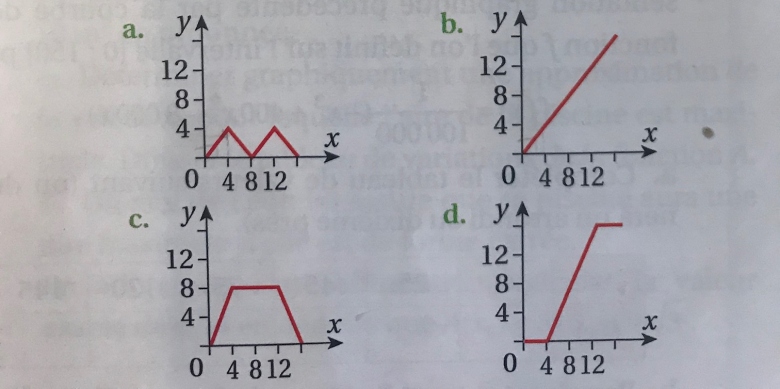
ABCD est un carré de côté 4 et de centre 0. E est un point parcourant le carré en suivant le chemin D-A-B-C-D.
Associer à chaque figure( 1 à 4) le graphique (a à d) représentant l'aire coloriée située à l'intérieur de ce carré lorsque E décrit le parcours D-A-B-C-D.
J'ai d'abord rangé l'aire des figures dans l'ordre décroissant :
fig 2 > fig 3 > fig 4 > fig 1
Puis j'ai rangé les graphiques dans l'ordre décroissant, c'est-à-dire lorsque l'aire est entre 0 et 4 est de la plus grande à la plus petite :
c > b > a > d
J'obtiens donc que :
c) fig 2
b) fig 3
a) fig 4
d) fig 1
Merci
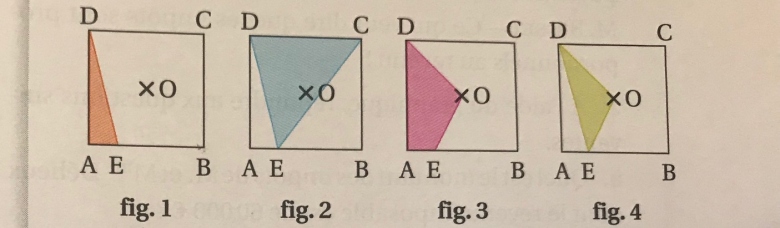
Bonjour,
j'ai rangé les graphiques dans l'ordre décroissant
rigoureusement aucun rapport
c'est-à-dire lorsque l'aire est entre 0 et 4 certainement pas
pour chacune des figures et indépendamment
l'aire peut varier de 0 à au maximum l'aire totale de tout le carré = 4² =16
chacune des figures et chacun des graphiques représente une situation dynamique : ce qu'il se passe quand E se déplace
et selon la figure les variations de cette aire sont différentes
certaines ne font que croitre
d'autres croissent puis décroissent etc
c'est les variations qu'il faut examiner, comment varie l'aire de chaque figure quand E se déplace. sur cette figure
à suivre : animation d'une des figures à titre d'exemple
et donc l'énoncé est faux (la figure 1 ne correspond à aucun des graphiques)
ce n'est pas parce que c'est dans un livre que c'est forcément vrai, même dans les livres il y a des erreurs...
Bonsoir,
Oui, pour moi, seule la figure 4 trouve chaussette à son pied.
Pour la figure 3, on ne sait pas ce qui doit être colorié quand le point E passe sur le côté [BC].
On continue à s'accrocher au sommet A ou pas ?
Si oui, le polygone dont l'intérieur est colorié est un peu biscornu ; mais on trouve aussi chaussure à son pied.
Reste 2 figures et 2 graphiques orphelins.
Dommage, ça aurait pu être un exercice intéressant.
l'interrogation est déja valable pour la figure 1 !!
en fait on ne sait pas comment évoluent exactement les figures quand E se déplace, ce n'est pas défini explicitement dans l'énoncé "les aires coloriées" c'est flou de chez flou et il faut deviner !
j'ai pris comme hypothèse pour la figure 1 qu'il s'agissait du triangle DAE
mais cette hypothèse est peut être fausse !
(et c'est plus difficile de faire l'animation si c'est autre chose ! car le nombre même de sommets du polygone varie selon le côté sur lequel se trouve E)
nouvelle hypothèse sur la façon dont varie la figure 1 :
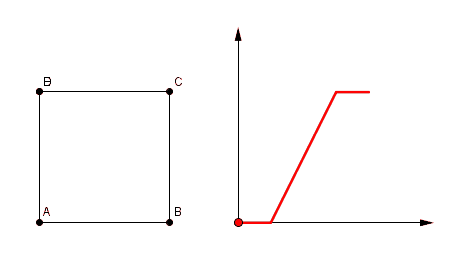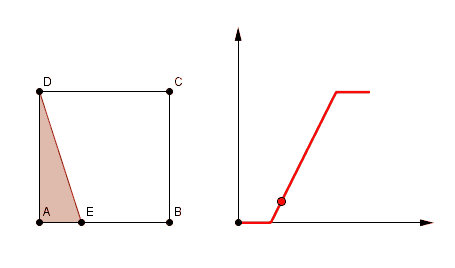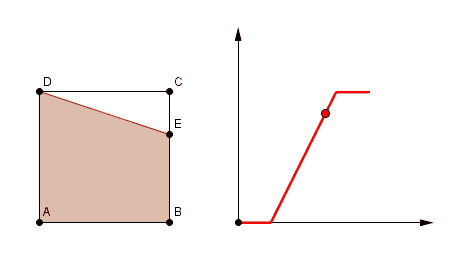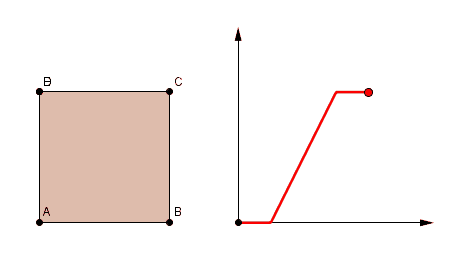
et pareil pour la figure 3 si on admet que le polygone reste "accroché" selon le même principe aux côtés du carré au fur et à mesure
en tout cas avec cette nouvelle hypothèse il y a presque les 4 "matchs" sur 4 !
seule la figure 2 ne correspond pas exactement, même si "ça ressemble" à la courbe restante une fois les autres trouvées (qui elles sont exactes du coup)
mathafou @ 24-01-2020 à 19:15
*** reste de la citation inutile ***
Merci beaucoup pour les animations je comprends mieux. C'était pas du tout clair. Du coup il suffit de regarder les variations, en fonction du triangle DAE.
Sylvieg @ 24-01-2020 à 18:28
*** reste de la citation inutile ***
de plus caduque vu ma réponse ultérieure...
Merci pour la réponse
je ne comprends même pas comment certains graphiques peuvent aller jusqu'à 16 = aire du carré puisque les figures ne sont jamais le carré
en fait pour la figure 3 il faut considérer l'aire balayée par le segments [OM] depuis le segments [OD] et en tournant dans le sens positif ...
figure 3 : oui, et donc quand ce segment a fait un tour complet il a balayé tout le carré = 16
et même la figure 1 (la deuxième hypothèse, très certainement la bonne vu que la courbe correspond) quand E arrive sur le segment CD, le polygone (un pentagone DABCE) remplit le carré, donc aire = 16 tout le temps que E parcourt [CD] (le plateau à la fin)
pour la figure Geogebra :
je définis mon carré ABCD
je définis un curseur t variant de 0 à 16, abscisse "curviligne" de E le long du périmètre
(il est masqué pour la figure)
puis les coordonnées de E par une expression conditionnelle sur t (avec des SI), en relatif par rapport aux sommets du carré :
E = Si[t < a, D + (0, -t), Si[t < a + b, A + (t - a, 0), Si[t < 2a + b, B + (0, t - a - b), C - (t - 2a - b, 0)]]]
(en fait mon carré est un rectangle de dimensions a et b, tant qu'à faire ...)
dans chaque cas je définis le polygone et son aire S (encore une expression conditionnelle)
ensuite pour afficher le graphique :
je définis un point origine arbitraire I (nom caché) et deux vecteurs matérialisant les axes
et le point P = I+(t/4, S/4) (idem, nom caché, divisés par 4 sinon trop grands, "facteur d'échelle")
je demande de tracer le lieu de P
et c'est fini
il n'y a plus qu'à créer un GIF animé à partir de ça (menu adéquat de Geogebra)
aboudesouffle : "en fonction du triangle DAE"
bein non vu que ce n'est un triangle que quand E est sur [AB] !!
au départ quand E est encore sur [DA] l'aire est nulle ("triangle aplati, dégénéré")
sur [AB] c'est le triangle ADE
sur [BC] c'est le trapèze DABE
et sur [CD] le pentagone DABCE, indiscernable du carré tout entier.
nota : totalement inutile (donc nuisible) de citer le message entier auquel tu réponds
pour répondre c'est le bouton Répondre écrit Répondre dessus,
ou ne rien faire du tout si la zone de saisie de réponse est déja présente
et taper sa réponse dans cette zone de saisie et rien d'autre.
mathafou : merci ... mais j'ai trouvé encore plus mieux bien (en fait j'avais déjà fait une figure de ce genre) car beaucoup plus efficace :
créer le carré ABCD avec A = l'origine du repère (mais est-ce vraiment nécessaire ?)
créer le point M point sur objet sur le bord du carré q1 (il reste sur le bord et se retrouve bloqué à l'intérieur si on le créer à l'intérieur)
créer le nombre paramètrechcemin(M) créer un réel (que je note t) variant dans l'intervalle [0, 1] quand M parcourt le carré)
créer le triangle t1 (un de ceux qu'on veut) (t1 = aire du triangle t1)
puis comme toi créer le point (que je note P) : P = (4t, t1) puis lieu(P, M)
je multiplie t par 4 pour un carré de côté 4 (ou non : ça étale sur l'axe des abscisses tout simplement ... et en général de toute façon je prends toujours une figure "unité" : ici un carré de côté 1 : il est toujours aisé de multiplier par coefficient d'agrandissement/réduction)
je t'aurai bien montrer ... malheureusement pour exporter un GIF qui soit animé il faut exclusivement un curseur
c'est beaucoup plus mieux bien car une fois j'avais fait comme toi avec un paramétrage à l'aide de SI ... mais que c'est pénible .... mais obligatoire si on veut l'exporter en GIF animé
si tu as besoin d'info fais moi signe ... mais c'est trop cool !!! 

bien vu la fonction parametrechemin() !!
ceci dit pour un Gif il faut partir d'un curseur, tu l'as bien remarqué.
en tout cas si tu as A = l'origine = origine du repère pour le graphique, ça se superpose mochement
il vaut mieux dissocier les deux en choisissant soit un carré "flottant " à partir de A libre, soit un repère du graphique flottant comme j'ai fait.
je ne vois pas comment tu peux échapper aux "Si" car la forme même (le nombre de sommets) du polygone peint dépend de la position de E (sur quel côté il est)
il est vrai qu'avec parametrechemin() il n'y a qu'une seule structure de "Si" : le polygone.
ce n'est pas toujours un triangle pendant le déplacement de E !!!
alors en fait j'ai déplacé mon carré et ça ne pose pas de pb finalement :
cordonnées de A = (-1.5, 0) et carré direct de côté 1 (en créant bien les points B, C et D puis polygone)
pour les figures les triangles ne posent aucun pb : création dans l'ordre des points DAE, CDE et DOE et j'obtiens toujours des triangles et les graphiques a, c et d (ou presque)
seule le quadrilatère DAEO pose pb car il est croisé à un moment avec ggb et je suppose que c'est :
je ne comprends même pas comment certains graphiques peuvent aller jusqu'à 16 = aire du carré puisque les figures ne sont jamais le carré
en fait pour la figure 3 il faut considérer l'aire balayée par le segments [OM] depuis le segments [OD] et en tournant dans le sens positif ... je pense
je trouve lamentable de ne pas préciser quelles sont exactement les figures considérées

une dernière remarque :
E = Si[t < a, D + (0, -t), Si[t < a + b, A + (t - a, 0), Si[t < 2a + b, B + (0, t - a - b), C - (t - 2a - b, 0)]]]
on peut (peut-être) faire mieux aussi (en tout cas ça marche avec des nombres mais je n'ai jamais essayé avec des points) et des booléens mieux ... meilleurs !!!
E = [D + (0, -t)] * (0 < t < a) + [A + (t - a, 0)] * (a < t < a + b) + [B + (0, t - a - b)] * (a + b < t <2a + b) + [C - (t - 2a - b, 0)] * (2a + b < t < 2a + 2b)
PS : j'ai mis des crochets pour rendre lisible l'expression mais il faut bien sur n'utiliser que des parenthèses
je ne sais pas trop ce que ça donne le produit d'un élément par un booléen
vu que c'est par principe douteux, j'aurais tendance à éviter !! 
avec de nombres ça marche et je l'utilise pour définir des fonctions par morceaux
f(x) = (x^2 + 1) * (x <= 0) + (2x + 1) * (x >=0) est parfaitement définie
en géométrie on peut multiplier des points par des nombres
I = (2A + 3B)/5 est le barycentre de (A, 2) et (B, 3)
donc je n'ai pas encore essayé mais à priori pourquoi pas ... même si un booléen n'est effectivement pas un nombre (mais souvent traduit par les nombres 0 et 1)
et avec un logiciel il n'y a rien de douteux ... juste un code qui s'exécute ou pas ...

breaking news : ça marche !!! et je le mets dans mes outils !!

si on veut que "ça colle" entre les graphiques et les figures
figure 1 : un polygone variable (ma deuxième animation de la figure 1 !!!)
et on ne va pas dire qui est qui pour ne pas faire l'exo à la place du demandeur!!! graphique OK et exact
figure 2 : clairement un triangle variable mais le graphique est faux (même remarque je ne dis pas lequel)
l'erreur ressemble plus à une erreur d'inattention de celui qui a fabriqué l'exo : c'est "presque ça"
figure 3 : un polygone variable (balayage du carré par le rayon OE), graphique OK et exact
figure 4 : un triangle, graphique OK et exact