Inscription / Connexion Nouveau Sujet
Avec Python
Bonjour à tous,
Notre professeur de mathématiques nous a donné cet exercice à faire sans nous avoir donné un cours du coup je ne comprends pas bien ce que nous devons faire, pouvez vous m'aiguiller s'il vous plait afin que je comprenne ce que je dois faire et si mes réponses sont justes ou pas ?
Voici l'énoncé de l'exercice
Dans cet algorithme, les variables xA, yA, xK, yK contiennent des nombres réels.
Algorithme : xB 2 X xK - xA
yB 2 X yK - yA
1 a. Si xA, yA, xK, yK contiennent respectivement - 1, 5, 2, 3 avant exécution de l'algorithme, que contiennent les variables xB et yB après exécution ?
b. Placer dans le plan les points a(xA ; yA), K(xK ; yK) et B(xB ; yB).
c. Que représente le point B par rapport à A et K ?
d. Quelle conjecture peut-on faire sur le rôle de cet algorithme ? Le démontrer.
2. Le script suivant en Python définit une fonction.
def sym(xA, yA, xK, yK) :
return (2*xK - xA, 2*yK - yA)
a. Quel est le nom de cette fonction ?
Combien a t'elle d'arguments ?
b. Quelle sortie obtient on après exécution de l'instruction sym (-1, 5, 2, 3)?
c. Quel est le rôle de cette fonction ?
Dites moi si je suis sur la bonne voix pour le petit a et b de la question 1
a) xB 2 x 2 - -1 xB = 5
yB 2 x 3 - 5 yB = 1
b) A(-1 ; 5), K(2 ;3), et B(5 ; 1)
je réécris ton algorithme (j'ai mis du temps à le déchiffrer ^^)
Algorithme :
xB <-- 2 * xK - xA
yB <-- 2 * yK - yA
1c) tu as placé les points ?
que constates-tu ?
Ryota
je réécris ton algorithme (j'ai mis du temps à le déchiffrer ^^)
Algorithme :
xB <-- 2 * xK - xA
yB <-- 2 * yK - yA
1c) tu as placé les points ?
que constates-tu ?
Oui je n'avais pas mis les flèches j'ai eu un bug avec mon clavier par contre le reste était bon c'est bien 2* Xk-Xa et 2*Yk-Ya c'est écris ainsi dans le manuel
Justement je ne comprends pas le petit c ni le reste des questions suivante je ne sais pas ce que je dois faire ensuite car notre professeur ne nous a rien expliqué
Ryota
je réécris ton algorithme (j'ai mis du temps à le déchiffrer ^^)
Algorithme :
xB <-- 2 * xK - xA
yB <-- 2 * yK - yA
1c) tu as placé les points ?
que constates-tu ?
Oui je n'avais pas mis les flèches j'ai eu un bug avec mon clavier par contre le reste était bon c'est bien 2 * xK - xA et 2 * yK - yA c'est écris ainsi dans le manuel
Justement je ne comprends pas le petit c ni le reste des questions suivante je ne sais pas ce que je dois faire ensuite car notre professeur ne nous a rien expliqué
tu as placé les points dans un repère orthonormé ?
Je ne comprends pas pourquoi un repère orthonormé ? C'est quoi d'ailleurs ?
merci de ne pas citer les messages précédents, ça alourdit le fil inutilement.
je ne comprends pas le petit c
quand tu auras placé les points, tu dois remarquer quelque chose...
Si ce que j'ai copié sur le net est juste car je nous n'avons pas encore appris a faire un plan orthonormé voir un plan tout court même.
Je dirais que les points A et B sont en face l'un de l'autre alors que le point K non.
Bonjour,
En passant... (Carita reprendra la main dès son retour)
As-tu placé les 3 points A(-1 ; 5), K(2 ;3) et B(5 ; 1) dans un repère ? Tu sais ce que cela est, j'espère qu'un repère sur ta feuille plane : un point origine O et deux axes gradués pour les abscisses et les ordonnées  ou ce qui revient au même (O;I;J) ou encore (O;
ou ce qui revient au même (O;I;J) ou encore (O; .
Montre nous la figure que tu as obtenue.
Je ne comprends pas ce que tu veux dire quand tu écris :
Je dirais que les points A et B sont en face l'un de l'autre alors que le point K non.
Bonjour,
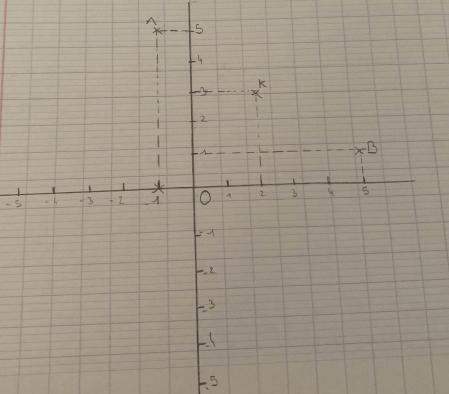
Voici une photo de mes réponses ainsi que du plan que j'ai essayé de faire sachant que nous n'avons fait aucune leçon la dessus.
Pour la question 1 c) je dirais que le point B et A forme une droite dont le point K est son milieu.
Mais ensuite je ne sais pas ce que je dois faire car nous n'avons fait aucun cours.
bonjour
1b) oui, tes points sont bien placés.
c. je dirais que le point B et A forme une droite un segment dont le point K est son milieu.
en effet, le point K est le milieu du segment [AB]
(pas de la droite (AB) car une droite n'a pas de milieu)
mais la question est posée ainsi : Que représente le point B par rapport à A et K ?
réponse : le point B est le ..... ?
et ne me dis pas que tu n'as pas fait de cours ^^ (tu as appris tout ça en 5ème)
d. Quelle conjecture peut-on faire sur le rôle de cet algorithme ? Le démontrer.
je te laisse un peu réfléchir sur l'utilité de l'algorithme
si tu ne vois pas : refais tourner l'algorithme avec xA=-4 yA=1 xB=-2 yB=4
puis place les points A, B et K; que constates-tu à nouveau ?
pour la démonstration, on verra quand tu auras trouvé la conjecture.
c) Oui j'ai écris trop vite c'est un segment dont K est son milieu.
On peut en déduire que le point B est l'opposé du point A.
d) pour la d j'ai refais les calculs qui m'avait permis de trouver la valeur de xB et yB
du coup en changeant les données cela donnerait cela
xB <-- 2*2-4
xB =8
yB <-- 2*47-1
yB = 7
l'autre point est en dehors du segment.
c) le terme exact est symétrique.
le point B est le symétrique du point A par rapport au point ....?
si tu veux faire une petite révisions, c'est par ici ![]() Symétrie
Symétrie
d) avec xA=-4 yA=1 xK=-2 yK=4
xB <-- 2*2-4
xB =0
yB <-- 2*47-1
yB = 7
donc B(0;7)
place B, ça devrait aller mieux 
c) que représente le point B par rapport au point A est que le point B est symétrique du point A est que le point K est le milieu du segment [AB].
C'est bien cela ?
d)xB <-- 2*-2-4
xB = 0
yB <-- 2*4-1
yB = 7
Donc B (0;7)
j'ai refais le plan avec le nouveau point est que c'est bien cela ?
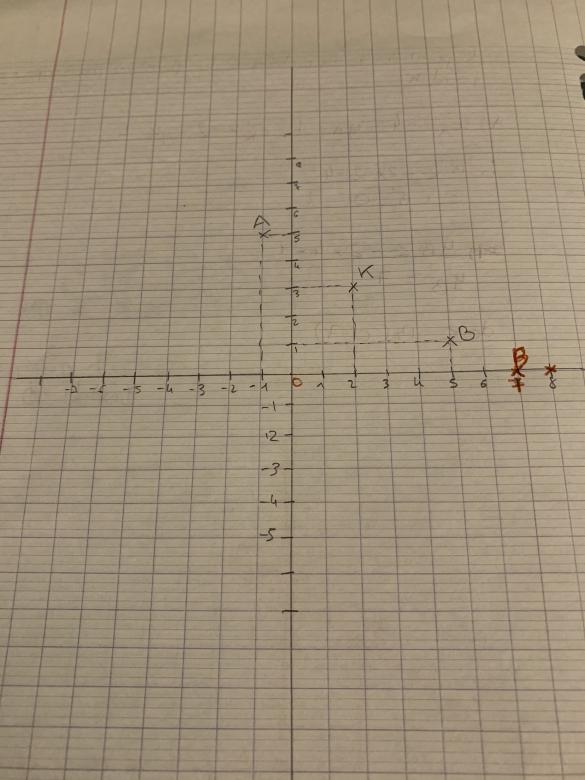
c) le point B est symétrique du point A par rapport au point K --- cette précision est indispensable.
d) résultat de l'expérience :
on conjecture (c'est-à-dire on émet l'hypothèse), que
cet algorithme permet de calculer les coordonnées du point B, symétrique du point A par rapport à K
maintenant on doit le démontrer !
dire que le point B est symétrique du point A par rapport au point K,
c'est dire que K est le milieu du segment [AB] ---- ce que tu as dit.
tu vas utiliser un chapitre du cours qui permet de calculer les coordonnées d'un point milieu :
on pose A(xA; yA) et B(xB; yB)
à toi !
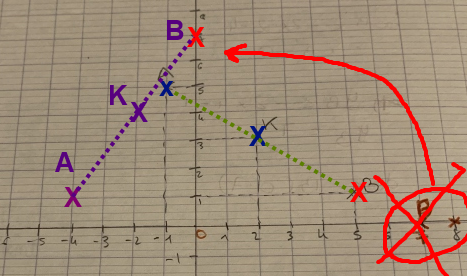
Petite remarque en passant....
La figure fournie par Ryota à 18h15 est... très fausse 
Si on part des points A(-4;1) et K(-2;4), on obtient bien comme symétrique du point A par rapport à K, le point B de coordonnées (0;7)... qui est sur l'axe des ORDONNÉES.
justement nous n'avons pas encore fait de cours la dessus j'ai trouvé cela sur le net je ne sais pas si c'est juste.
A (xA ; yA) B(xB ; yB)
A (-1 ; 5) B (5 ; 1)
Les coordonnées du milieu du segment [AB]
sont (xA + xB/2 ; yA + yB/2)
(-1+5/2 ; 5+1/2)
K est le milieu de [AB] donc AK = KB
on a AK (xK - xA ; yK - yA) et KB (xB - xK; yB - yA).
Comme ces 2 vecteurs sont égaux. Ils ont les mêmes coordonnées par conséquent.
xK -xA = xB - xK et yK - yA = yB- yK ; soit 2xK = xA+ xB et 2yk = yA + yB
donc xK = xA+xB/2 et yK = yA+yB/2
en effet il y a eu un bug avec mes deux photos j'ai envoyé la mauvaise photos et supprimé la bonne les bons points sont bien comme ZEDMAT a gentiment corrigé sur la photo erreur
c'est la bonne formule, mais avec des ( ) obligatoires pour que ce soit juste
Les coordonnées du milieu K du segment [AB] sont ( (xA + xB) /2 ; (yA + yB ) /2) ---- oui
-----
on a AK (xK - xA ; yK - yA) et KB (xB - xK; yB - yA). ---- non, là tu pars sur les vecteurs, il est inutile de passer par là.
-----
je reprends : avec la formule du cours que tu as citée juste au-dessus, on a donc
xK = (xA + xB) / 2
yK = (yA + yB) / 2
manipule simplement ces égalités pour retrouver ce qu'il y a dans l'algorithme.
xB = .....?
yB = ....?
d) Les coordonnées du milieu K du segment [AB] sont ( (xA + xB) /2 ; (yA + yB ) /2)
par conséquent
xK = (xA + xB) / 2
yK = (yA + yB) / 2
xK = (-4+0)/2
xK = -2
yK (1+7)/2
yK = 4
non
on oublie tout nombre à présent : on ne travaille qu'avec des variables
le calcul que j'attends, tu y étais presque ici :
.... soit 2xK = xA+ xB et 2yk = yA + yB
compare ce que tu as écrit et l'algorithme.

que reste-t-il à faire pour arriver aux formules de l'algo ?
il ne faut pas mettre les nombres je croyais donc si je reprends tout
les coordonnées du point K qui est le milieu du segment [AB] sont ((xA+xB)/2;(yA+yB)/2)
xK = (xA+xB)/2
yK =(yA+yB)/2
soit 2xk = xA+XB et 2yK= yA +yB donc xK = xA+xB/2 et yK = yA+ yB/2
est ce que c'est cela ?
dans l'algo tu as
xB <-- 2 * xK - xA
yB <-- 2 * yK - yA
donc tu dois établir
xB = 2 * xK - xA
yB = 2 * yK - yA
xK = (xA+xB)/2
yK =(yA+yB)/2 oui
2xk = xA+XB
2yK= yA +yB oui
d'où
xB =
yB =
je suis perdu la je ne comprends plus trop
xB = 5 et yB = 1 c'est ce qu'on a trouvé pour le petit a de l'exercice 1 non ?
ou c'est xB = 0 et yB = 7 ?
on a dit : plus de valeurs particulières !
que des variables.
tu sais quand même comment passer de 2xK = xA+xB à xB = 2 * xK - xA
non je ne sais pas du tout puisque notre professeur nous a donné cet exercice sans nous avoir fait une leçon avant c'est pour cela que je ne comprends pas ce qu'il faut faire.
pas besoin de cours pour ça, seulement appliquer les règles de calcul littéral
si j'écris a = b + c
tu en déduis que c = ....?
ah bon ?
Je suis désolé je dois vous paraître pénible, mais contrairement aux autres élèves je n'ai pas eu une scolarité normal j'ai du subir deux grosses opérations du cœurs qui ma privé d'énormément de cours que je n'ai pas pue récupérer pour la plus part du coup je suis en retard sur certains sujets
si a = b+c
je dois en déduire que c = a- b ? ou ce n'est pas ça
2xK = xA+ xB
xB = 2* xK-xA
2yK = yA+yB
yB = 2*xK-yA
je compatis avec ta situation,
et je n'ai jamais dit que tu es pénible, juste que tu es capable, avec ce que tu connais déjà depuis longtemps, de faire ce que tu as fini par faire 
oui, c'est la bonne réponse.
conclusion de notre démarche :
si K est le milieu de [AB], c'est-à-dire si B est le symétrique de A par rapport à K
alors, on a bien : xB = 2* xK-xA et yB = 2*xK-yA
on a ainsi démontré notre conjecture selon laquelle l'algo calcule les cordonnées du symétrique B du point A par rapport à K.
2) je te laisse relire le cours que tu as sur python,
ou à défaut faire quelques recherches internet pour découvrir l'instruction def
il y en a beaucoup sur le net ! en voici une prise "au hasard" ![]()
les questions du 2) ne sont pas très difficiles.
je dois couper pour l'instant, je reviens demain pour continuer l'aide,
sauf si Zedmat souhaite prendre le relais.
bonne soirée !
non je ne vous citez pas en disant cela mais j'ai eu malheureusement des réflexions très blessant à ce sujet.
Donc si je résume entièrement le petit d et que je me m'égare pas
La conjoncture qu'on peut faire sur le rôle de cet algorithme est que les coordonnées du symétrique B du point A par rapport à K car les coordonnées du milieu K du segment [AB] sont ((xA+xB)/2 ; (yA +yB)/2)
xK = (xA+xB)/2
yK =(yA+yB)/2
soit 2xk = xA+XB
2yK= yA +yB
donc xB = 2* xK-xA et yB = 2*xK-yA
est ce que c'est cela et est ce que je dois inclure l'autre segment dans mon plan A(-4,1) K (-2,4) et B(0,7) ?
merci beaucoup
j'ai fais l'exercice 2 pourriez vous me dire vite fait si c'est bon
2)a. le nom de cette fonction est symétrique et contient deux argument A et K.
b. La sortie qu'on obtient après l'exécution de l'instruction sym (-1,5,2,3) est que
(2*2-1, 2*3-5)
c. le rôle de cette fonction est de trouver les coordonnées du point B.
d) conjecture :
cet algorithme permet de calculer les coordonnées du point B, symétrique du point A par rapport à K --- (et c'est tout)
démonstration :
dire que le point B est symétrique du point A par rapport au point K, revient à dire que K est le milieu du segment [AB]
montrons que K est le milieu du segment [AB]
soit A(xA; yA) et B(xB; yB)
xK = (xA+xB)/2
yK =(yA+yB)/2
soit 2xk = xA+XB
2yK= yA +yB
donc xB = 2* xK-xA et yB = 2*xK-yA
on retrouve bien les instructions de l'algorithme.
conclusion : la conjecture est démontrée, à savoir :
cet algorithme permet de calculer les coordonnées du point B, symétrique du point A par rapport à K,
lorsqu'on lui fournit les coordonnées des points A et K.
bon, là, je coupe pour de bon 
a+
def sym(xA, yA, xK, yK) :
return (2*xK - xA, 2*yK - yA)
2)a.
le nom de cette fonction est symétrique
et contient deux argument A et K. --- non, compte combien il y a de données dans les parenthèses après "sym"
b. La sortie qu'on obtient après l'exécution de l'instruction sym (-1,5,2,3) est que
(2*2-1, 2*3-5) ---- en rouge, erreur de signe
c. le rôle de cette fonction est de trouver les coordonnées du point B. ---- oui

eh bien tu vois ! tu en sais des choses pour quelqu'un qui n'a pas eu de cours ! 
merci beaucoup.
J'ai fais l'exercice 2 sans me poser aucune question je suis choqué moi même encore une fois merci beaucoup pour votre aide c'est vraiment gentil à vous.
merci beaucoup
j'ai fais l'exercice 2 pourriez vous me dire vite fait si c'est bon
2)a. le nom de cette fonction est symétrique et contient deux argument A et K.
Non ,pas vraiment.
Tu as
def sym(xA, yA, xK, yK) :
donc le nom de la fonction est sym( )[/b]
et si tu regardes bien, entre les parenthèses, il y a...4 variables donc cette
fonction requière 4 arguments.
b. La sortie qu'on obtient après l'exécution de l'instruction sym (-1,5,2,3) est que
(2*2-1, 2*3-5)
ce qui fait ?? (3;1)
Le calcul à la main ne te donnait pas cela mais (5;1) (et on t'a dit que cela était exact=> erreur (ici)
c. le rôle de cette fonction est de trouver les coordonnées du point B.
OUI
Bon pendant que je rédigeais ma réponse , Carita a poursuivi. Pas grave... tu as 2 avis 
Comme on a dit la même chose  , pas de problème.
, pas de problème.
As tu installé le langage python sur ton ordinateur et saisi le script de l'énoncé pour vérifier tes réponses ? Cela serait bien (pour toi) d'essayer si tu ne l'as pas fait.
Si tu veux, Carita ou moi pouvons t'aider à découvrir un peu python à travers ce premier exemple... mais ce sera pour demain de préférence 


