Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. SecondeForum de Maths Seconde Droites et systèmesTopics traitant de droites et systèmes [tout]Lister tous les topics de mathématiques

1 2 +

Niveau seconde
Partager :

Avec un guide (1)

Posté par
badeasy 19-03-13 à 14:13

f est la fonction affine définie par :
f(x) = 2x-3.
Dans un repère orthonormé, d est la droite qui représente la fonction f.
On donne les points :
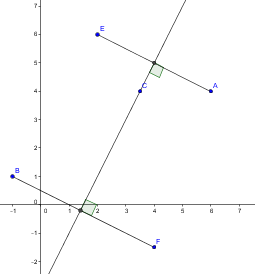
A (6;4), B (-1;1), C (7/2 ; 4) , E (2;6) , F (4;-3/2)
a) Construire la droite d et placer les points définis.
b) Le point C appartient-il a la droite d ?
c) Les points E et F sont-ils alors les symétriques respectifs des points À et B par rapport à d ?

Posté par
heklare : Avec un guide (1) 19-03-13 à 14:20

Bonjour

vous ne dites  ni bonjour ni merci

en outre vous ne dites pas  ce que  vous avez déjà réalisé ni où sont vos difficultés

pour aider  oui; pour le faire  non

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 14:22

Bonjour Pardonnez moi mais j'ai écrit ça vite fait

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 14:24

Pour la a je ne sais pas si c'est 6 en ordonnée ou en abscisse je confond toujours

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 14:26

Et pour les fraction on fait comment ?

Posté par
heklare : Avec un guide (1) 19-03-13 à 14:31

A \dbinom{a}{b} a est suivant le  premier vecteur c'est l'abscisse

b est suivant  le second vecteur  c'est l'ordonnée  

les coordonnées d'un point  sont  toujours (abscisse ; ordonnée)  ou (selon x ; selon y)

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 14:37

Ok merci

Posté par
heklare : Avec un guide (1) 19-03-13 à 14:41

de rien

sans commentaire la figure

Avec un guide (1)

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 14:44

Cest bon ça me fait exactement ça j'ai compris.  Le point C appartient à la droite mais pour la b on justifie comment ?

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 14:45

Merci

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 14:45

Il faut faire des calculs je croix

Posté par
heklare : Avec un guide (1) 19-03-13 à 14:57

un point appartient à une courbe  si et seulement si ses coordonnées vérifient  l'équation de la courbe

le point C \in d \iff  y=f(\frac{7}{2})

vous calculez  f(\dfrac{7}{2})  si vous trouvez 4 c'est bon pour l'appartenance

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 15:02

J'ai pas compris

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 15:07

F(7/2) = 4 ?

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 15:08

Comment on fait pour trouver 4 par le calcul

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 15:12

Pour la c il faut calculer la mediatrice ou on dit juste une définition ?

Posté par
heklare : Avec un guide (1) 19-03-13 à 15:13

l'équation de la droite  est y=2x-3 l'ordonnée du point de  la droite d'abscisse  \dfrac{7}{2} est : y=2\times \dfrac{7}{2}-3 =\dots

je vous laisse le calcul et la conclusion

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 15:18

À oui.
y = 2 x 7/2 - 3 = 4

Posté par
heklare : Avec un guide (1) 19-03-13 à 15:22

et la conclusion ?

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 15:26

Il ne faut rien faire d'autre ?

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 15:26

Donc C appartient à la droite d

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 15:34

Pour la b il ne faut pas dire en plus que c'est la meduatrice par rapport à la c ?

Posté par
heklare : Avec un guide (1) 19-03-13 à 15:54

que voulez-vous dire ?

pour b) vous avez dit que C appartenait à la droite  vous avez donc répondu à la question. point

pour c) il va falloir montrer que d est la médiatrice de [AE] et aussi celle de  {BF]


a) calculez les coordonnées du milieu de {EA]

b) vérifiez que ce point  appartient à d

c) donner un nom à l'intersection de d et (AE) par exemple  M

d) montrez que AMC est un triangle rectangle

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 15:56

Ou il faut le dire pour la c ? Mais je sais pas comment justifier

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 15:56

À ok pardon pour le message d'avant

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 16:02

Eu..

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 16:04

Pour le milieu on fait comment ?

Posté par
heklare : Avec un guide (1) 19-03-13 à 16:05

ce n'est pas tellement explicite

a)milieu d'un segment

si I est le  milieu de [AB]
x_{\text{I}}=\dfrac{x_{\text{A}}+x_{\text{B}}}{2}\qquad y_{\text{I}}=\dfrac{y_{\text{A}}+y_{\text{B}}}{2}

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 16:07

Mais pour ça il faut une figure non ?

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 16:13

Ça fait (4;5) ?

Posté par
heklare : Avec un guide (1) 19-03-13 à 16:14

oui et c'est cohérent avec le dessin

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 16:15

Il est bien sur la droite

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 16:17

Pour la d il faut faire un calcul ?

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 16:21

Sinon après in fait le même raisonnement pour [BF] ?

Posté par
heklare : Avec un guide (1) 19-03-13 à 16:22

oui  il faut calculer AM, AC et MC  sachant que

\text{AB}=\sqrt{\left(x_{\text{B}}-x_{\text{A}}\right)^2+\left(y_{\text{B}}-y_{\text{A}}\right)^2}


puisqu'il n'y a plus  l'orthogonalité au programme

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 16:31

Ça fait racine de 5 ?

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 16:32

Pour AI ?

Posté par
heklare : Avec un guide (1) 19-03-13 à 16:38

si vous avez appelé I le point d'intersection de la droite d avec (AE) on a bien AI= \sqrt{5}

  il est bien entendu qu'il faudra faire  de même pour montrer que F et B sont symétriques par rapport à d

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 16:49

J'ai trouvé racine de 5 , racine de 6,25 et racine de 57,25 maïs le dernier me paraît bizar

Posté par
heklare : Avec un guide (1) 19-03-13 à 17:00

AC=\dfrac{5}{2}

AI=\sqrt{5}

IM=\dfrac{\sqrt{5}}{2}

AI^2+IC^2=5+\dfrac{5}{4}=\dfrac{25}{4}

AC^2=\dfrac{25}{4}

Posté par
heklare : Avec un guide (1) 19-03-13 à 17:01

au lieu de IM lire IC

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 19:39

Ok et c'est tout après on fait pareil pour l'autre et puis cent bon ?

Posté par
heklare : Avec un guide (1) 19-03-13 à 19:42

c'est bien ce que  j'avais dit à 16 :38

remarque faites attention à l'orthographe

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 19:59

Ok et après on met rien d'autre quand ça c'est fait ?

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 20:24

comment vous avez fait pour trouver IC et IL parce que je ne trouve pas pareil

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 20:27

AC pardon

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 20:34

j'ai trouvé pour l'autre : (1.5;-0.25)

Posté par
heklare : Avec un guide (1) 19-03-13 à 20:38

\vec{AC}\quad \dbinom{\dfrac{7}{2}-6}{4-4}\quad \dbinom{-\dfrac{5}{2}}{0} \qquad AC=\dfrac{5}{2}

\vec{AI}\quad \dbinom{4-6}{5-4}\quad \dbinom{-2}{1} \qquad AI=\sqrt{5}

\vec{IC}\quad \dbinom{\dfrac{7}{2}-4}{4-5}\quad \dbinom{-\dfrac{1}{2}}{-1} \qquad AC=\dfrac{\sqrt{5}}{2}

Posté par
badeasyre : Avec un guide (1) 19-03-13 à 20:51

Ils sont ou les + ?

Posté par
heklare : Avec un guide (1) 19-03-13 à 20:54

quels + ? il faudrait être un peu plus explicite

1 2 +


Rechercher
Menu
Espace membre
9 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1741 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !