Bonjour !

J'ai des exercices de maths à faire en ligne sur la plateforme wims et j'aurais besoin d'aide pour un exercice. Je me demande si il n'y a pas un "bug" dans l'exercice car je suis quasiment sûre de mes calculs et pourtant il m'est impossible de trouver une réponse.
Je m'explique.

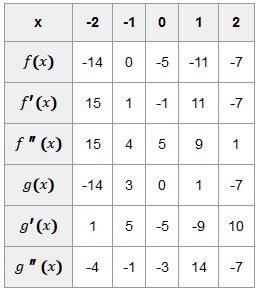
Nous avons un tableau qui nous présente les images de deux fonctions f et g ainsi que les images de leurs dérivées et dérivées seconde pour certains antécédents (-2 ; -1 ; 0 ; 1 et 2). Je joins le tableau à ce post. On nous dit ensuite que la fonction h est telle que h=f(g), et on nous demande de calculer h''(2).

Selon moi, voici le calcul pour obtenir h" :

h = f(g)

h' = (f(g))' = f'(g) * g'

h" = (f'(g) * g')' = (f'(g))' * g' + g" * f'(g) = f"(g) * (g')² + g" * f'(g)

Tout d'abord, est-ce juste ?

Si ça l'est, alors je ne comprends pas comment trouver le résultat avec le tableau. En effet on aura donc pour h"(2) :

h"(2) = f"(g(2)) * (g'(2))² + g"(2) * f'(g(2))
h"(2) = f"(-7) * 100 - 7 * f'(-7)

Or sur le tableau on n'a pas f(-7) car -7 ne fait pas partie des antécédents proposés.

Y a-t-il un moyen de trouver f(-7) ?

Je vous remercie d'avance, bonne soirée.

Marthe