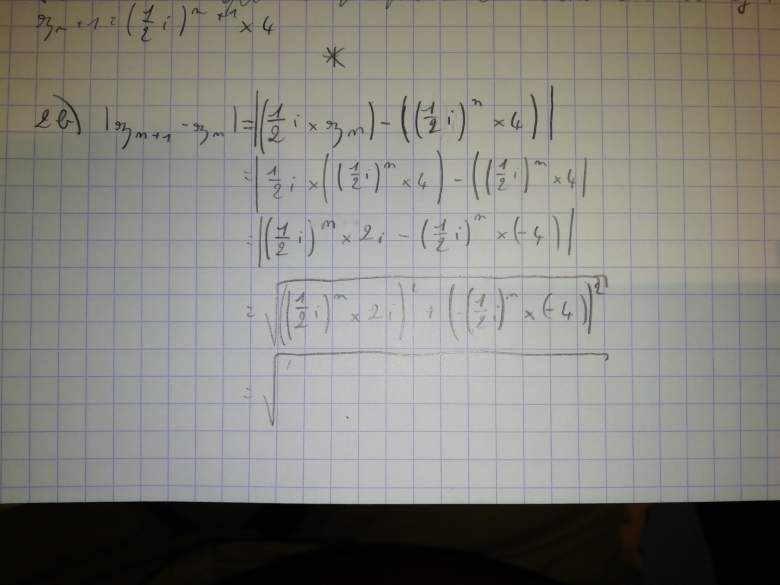Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Nombres complexesTopics traitant de nombres complexes [tout]Lister tous les topics de mathématiques
Niveau terminale
Calcul avec des complexes
Posté par romaingrc
Bonjour, j'ai un calcul à réaliser où la réponse nous est donné mais je n'arrive pas à y aboutir...
On nous demande:
|z(n+1)-z(n)|=2\sqrt{5}*\frac{1}{2^n}
Sachant que:
z(n+1)=\frac{1}{2}i*z(n)
z(n)=(\frac{1}{2}i)^n*4
Merci d'avance
Yzz @ 01-03-2020 à 18:11
Exprime z(n+1) - z(n)en fonction de n , en utilisant=(\frac{1}{2}i)^n*4)
Exprime z(n+1) - z(n)en fonction de n , en utilisant
c'est déjà ce que j'ai fait mais j'ai du faire des erreurs de calculs parce que je ne trouve pas le bon résultat...
Yzz @ 01-03-2020 à 18:11
LLLe mieux serait quand même d'avoir l'énoncé complet...
LLLe mieux serait quand même d'avoir l'énoncé complet...
Le plan complexe est rapporté à un repère orthonormé direct (0;u;v).
On considère la suite de nombres complexes z(n) définie sur N par z(0)= 4 et on note
On note A(n) le point du plan d'affixe z(n)
1°)a) calculez z(1), z(2) et z(3) et sur une figure placez les points A0,A1, A2, A3
b) calculez une mesure en radians de l'angle (OA0,OA2).
2°) a) montrer par récurrence que: pour tout n appartenant à N*,
b) montrer que: pour tout n appartenant à N*,
[...]
Citation :
c'est déjà ce que j'ai fait mais j'ai du faire des erreurs de calculs parce que je ne trouve pas le bon résultat...
Peux-tu donner le détail de tes calculs ?c'est déjà ce que j'ai fait mais j'ai du faire des erreurs de calculs parce que je ne trouve pas le bon résultat...