Calcul d'angle : exercice de mathématiques de école ingénieur

 Niveau école ingénieurPartager :
			        
Calcul d'angle
Posté par 
AsPiraTeuRe  31-10-21 à 17:32
Bonsoir à tous,

Pour illustrer la modélisation géométrique inverse d'un robot à deux degrés de liberté (robotique pour la mécatronique),  mon prof a utilisé un exemple, que je n'arrive pas à comprendre.

L'objectif est de déterminé l'angle Q2. 
Sans explication, il montre que : 

Pouvez-vous m'expliquer de quelle façon il arrive à ça ?

Je vous remercie d'avance.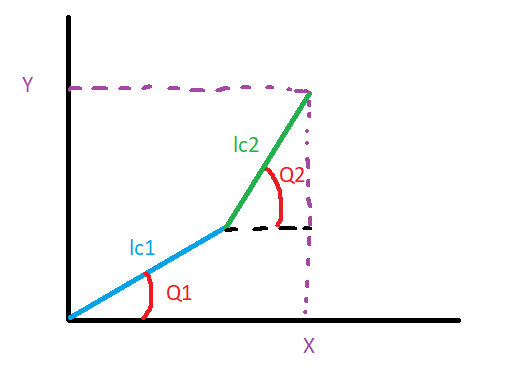

* Modération > Image recadrée pour éviter du vide à la fin du message  *
 Posté par 
philgr22re : Calcul d'angle  31-10-21 à 17:37
Bonjour,

Ecris ce que vaut cosQ2
 Posté par 
carpediemre : Calcul d'angle  31-10-21 à 17:38
salut

dommage de ne pas nous avoir mis des points aux extrémités des segments ...

il a simplement calculé un produit scalaire selon la formule 

 Posté par 
GBZMre : Calcul d'angle  31-10-21 à 17:39
Bonsoir,

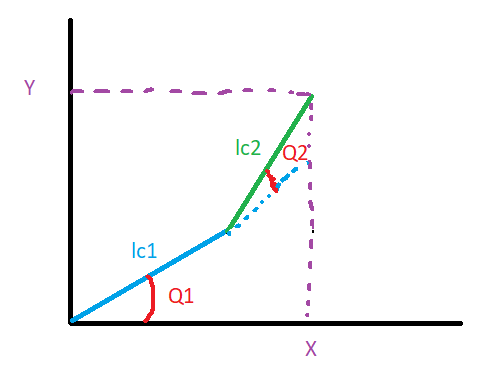
M'est avis que tu t'es trompé dans ton croquis, et que  n'est pas l'angle que tu indiques mais l'angle entre le prolongement de la première barre et la deuxième barre.

Le mot clé est alors : Al Kashi
 Posté par 
AsPiraTeuRere : Calcul d'angle  31-10-21 à 19:34
Merci pour vos réponses.

Je n'ai toujours pas trouvé. Pour vous répondre : 

GBZM @ 31-10-2021 à 17:39

Bonsoir,

M'est avis que tu t'es trompé dans ton croquis, et que  n'est pas l'angle que tu indiques mais l'angle entre le prolongement de la première barre et la deuxième barre.

Le mot clé est alors : Al Kashi

Oui, c'est une erreur de ma part. 

philgr22 @ 31-10-2021 à 17:37

Bonjour,

Ecris ce que vaut cosQ2

Je voulais utiliser les formules de trigo (soh cah toa), mais comme je n'ai pas un triangle rectangle pour l'angle Q2, je pense que ça va être difficile 

carpediem @ 31-10-2021 à 17:38

salut

dommage de ne pas nous avoir mis des points aux extrémités des segments ...

il a simplement calculé un produit scalaire selon la formule 

J'ai essayé, mais je ne trouve pas le bon résultat. Voici ce que j'ai fait : 

Voila voila 

Une autre idée m'est venu et peut-être plus simple  Et elle rejoint un peu l'idée de GBZM

On sait que (résultat prof)  : 

(1) : 

Avec pour objectif de trouver Q2 tel que :

(1) 

Et la je reste perplexe et je suis découragé pour trouver seulement cos(q2) 

Je pense que c'est la méthode qu'a utilisé mon prof
 Posté par 
AsPiraTeuRere : Calcul d'angle  31-10-21 à 19:39
J'ai oublié le nouveau schéma 

* Modération > Image recadrée pour éviter du vide en bas du message  *
 Posté par 
carpediemre : Calcul d'angle  31-10-21 à 19:56
il suffit de prendre pour u le vecteur représenté par le segment lc1 et pour v le vecteur représenté par le segment lc2 ...
 Posté par 
GBZMre : Calcul d'angle  31-10-21 à 20:52
Rassure-moi ... Al Kashi, tu connais, n'est-ce pas ?

Et le triangle dans lequel l'appliquer, il s'impose de lui-même ...
 Posté par 
AsPiraTeuRere : Calcul d'angle  31-10-21 à 22:44
GBZM @ 31-10-2021 à 20:52

Rassure-moi ... Al Kashi, tu connais, n'est-ce pas ?

Et le triangle dans lequel l'appliquer, il s'impose de lui-même ...

Le nom seulement  J'avais oublié son concept. J'ai compris. Merci.

carpediem @ 31-10-2021 à 19:56

il suffit de prendre pour u le vecteur représenté par le segment lc1 et pour v le vecteur représenté par le segment lc2 ...

Oui. Je ne sais pas ce que j'ai fait tout à l'heure 

Merci à vous deux 
  Posté par 
carpediemre : Calcul d'angle  01-11-21 à 09:44
de rien