Bonjour à tous,

Le sujet qui suit est un sujet lié aux probabilités.

Dans le cadre de recherches liées aux paris sportifs, je souhaite adopter une méthode des paris en chaînes par palier. J'ai essayé de traduire tout cela sous forme "mathématique" pour pouvoir ensuite vous poser mon problème.

Pour expliciter le texte plus haut et pour la suite, j'ai défini quelques variables :

Q est le nombre de paliers de la chaîne considérée.
M_1,0 est la mise initiale de la chaîne. On la note M par simplification.
N est le numéro du palier de pari en cours (j'appelle cela aussi "l'ordre du pari").
E_N est le nombre d'étapes consécutives à réaliser à l'ordre N pour passer au palier suivant.
c_N est la cote moyenne jouée sur le palier N. Les cotes étant multiplicatives, la moyenne est une moyenne géométrique et non arithmétique.
r_N est le "retour de cavage" qui détermine un rapport exprimé en pourcentage, soit la dernière mise du palier N-1 divisée par la première mise du palier N.
n_N est le nombre d'essais consécutifs à réussir au palier N pour passer au palier N+1.
n_N peut se calculer de deux manières :
? n_N = a/b où a est la valeur du dernier pari réalisé à l'ordre N-1 et où b représente la valeur du premier pari réalisé à l'ordre N.
? n_N = 1 / (1-r_N)
P_N(G) est la probabilité théorique de gagner une épreuve lorsqu'un pari est réalisé à l'ordre N.
P_N(G) peut est fixée de telle façon à ce que P_N(G) = 1/c_N
P_N(P) est la probabilité de perdre une épreuve au palier N. Celle-ci vaut 1-P_N(G).
Convention : nous décidons que n₁ = 1.



Pour expliciter les quelques variables ci-dessus, voici un exemple :
Soit une chaîne composée de Q=4 paliers,
La chaîne est notée ainsi :
(N=1) : 1 => 3 => 9 => 27
(N=2) : 9 => 27 => 81 => 243
(N=3) : 81 => 243 => 729 => 2187
(N=4) : 729 => 1300 => 2500 => 5000 => 10000

Alors : E₁=3 (car 3 flèches : il faut réussir 3 paliers consécutifs pour atteindre la fin du palier, c'est à dire 27 ?). E₂ = 3 ; E₃ = 3 et E₄ = 4.

n₁ = 1 (convention posée) ; n₂ = dernière mise de l'ordre 1 (palier 1) c'est à dire 27, divisée par première mise de l'ordre 2 (palier 2) c'est à dire 9 et donc 27/9 = 3.
n₃ = 243/81 = 3 ; n₄ = 2187/729 = 3.

Ensuite, le calcul des c_N :
c₁ = 3 (car on ne fait que des multiplications par 3 entre chaque pari).
c₂ = c₃ = 3 pour les mêmes raisons.
c4 = moyenne géométrique {1300/729 ; 2500/1300 ; 5000/2500 ; 10000/5000} = moyenne géométrique {1,78327 ; 1,92308 ; 2 ; 2} = racine_quatrième (1,78327 x 1,92308 x 2 x 2) = 1,9245.
Pour vérifier, si on réalise 729x 1,9245⁴ = 10 000 (quasiment, au vu des arrondis).



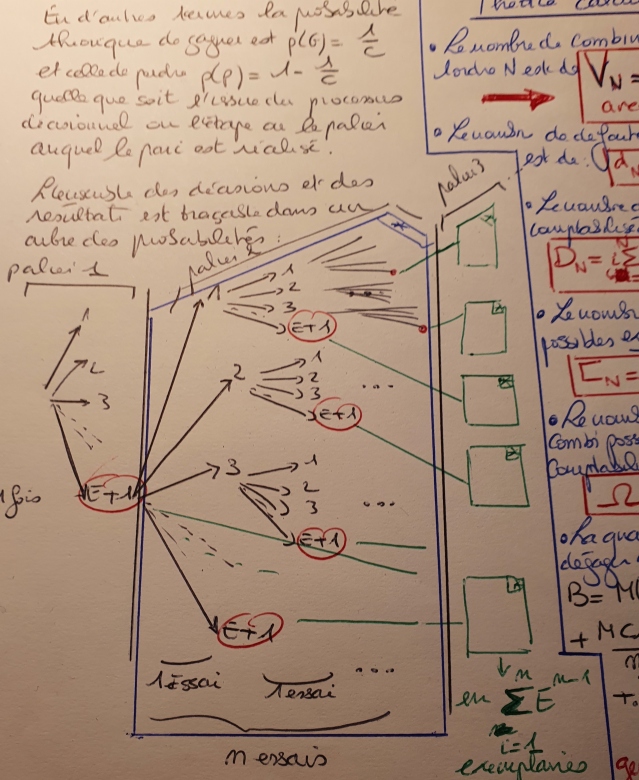
On appelle "combinaison", un ensemble d'évènements successifs.
Par exemple : GGPGGPGGGPGGGG (gagner, gagner, perdre, ...).
Si on reprend l'exemple en italique et en séparant par "|" les différents paliers, la combinaison idéale est la suivante : GGG|GGG|GGG|GGGG

La pire combinaison réalisable (en gagnant quand même le dernier palier) avec l'exemple en italique ci-dessus est la suivante : GGG|GGPGGPGGG|GGPGGPGGG|GGGPGGGPGGGPGGGG (en effet, on rappelle qu'à part le palier 4 [où E=4], il faut gagner consécutivement 3 fois à chaque autre palier et en n essais maximum (et on avait calculé que n=1 pour N=1 et n=3 pour N=2 et 3 et n=4 pour N=4, d'où le fait qu'il y ait nE "évènements" par palier, vu que c'est la pire configuration possible pour réussir la chaîne).

Ainsi, j'avais fait quelques calculs :

Le nombre de combinaisons gagnantes pour une chaîne comprenant Q paliers est de :
V_Q(somme de t=1 à t=n avec de E^(t-1)) x V_Q-1 avec V₁ = 1.

Le nombre de défaites exclusives à l'ordre N (et uniquement à l'ordre N) est de :
d_N = Eⁿ x V_N-1

Le nombre de défaites possibles pour une chaîne comprenant Q paliers est :
D_Q = somme de N=1 à N=Q des d_N

Le nombre total de combinaisons d'évènements possibles à l'ordre N est de :
C_N = V_N + d_N
(A noter que V_N se calcule comme V_Q en remplaçant toutes les occurrences de Q par N).

La quantité totale de bénéfices maximum à dégager à l'ordre N est de :
B_N = M(c₁^E1-1) + ((Mc₁^E1)/n₂)) x (c₂^E2-(T₂+1)) + ((Mc₁^E1c₂^E2)/(n₂n₃)) x (c₃^E3-(T₃+1))+ ... + M((c₁^E1 x ... x c_N-1^EN-1)/(n₂ x ... x n_N)) x ((c_N^EN-(T_N+1)) avec T_N le nombre de fois où E_N paris consécutifs n'ont pas été réussis au palier N (nota : si T_N = n_N, la chaîne entière a échoué).

Si c et E sont invariants sur toute la chaîne (donc quel que soit N), la formule ci-dessus peut se généraliser par l'expression B_{c,E fixes} = somme de N=1 à Q de : Mc^(p-1).E x (c^E - (1+T_N))

Le Gain maximum à dégager est G_Q = B_Q + M
(On distingue le bénéfice qui représente l'argent récupéré en plus de la mise initiale de la chaîne effectuée DU gain qui représente le bénéfice plus la mise de départ).

Si la chaîne est échouée (en d'autres termes, qu'on a pas réussi E_N paris consécutifs lors du palier N, avec au plus n_N essais), alors on perd M euros.

Voilà pour tous les calculs que j'ai pu effectuer de mon côté.

Un exemple d'arbre de probabilité que j'obtiens est joint dans le message (pour la configuration donnée en exemple italique). Ici "1" désigne "P" , "2" désigne "GP", "3" désigne "GGP" et "4" désigne "GGG".

La question que je me pose est vraiment complexe, et je comprends que vous y mettrez du temps à répondre :

Comment calculer l'espérance mathématique d'une chaîne de Q paliers (sans passer par Excel, c'est beaucoup trop long pour certains arbres) pour toutes les configurations possibles (c'est à dire, tous les M, E_N, c_N, n_N, P_N(G) et P_N(P) possibles ?

Je suis conscient que je vous demande un travail de titan.

J'ai fait l'exercice avec Excel, mais il me faut parfois près de une heure pour établir toutes les combinaisons... C'est pour ça que je préfère directement passer par une approche mathématique

Merci de votre aide, je n'hésiterai pas à venir clarifier tous les soirs mon énoncé si vous avez des questions.

Un grand merci à vous !