Inscription / Connexion Nouveau Sujet
Calcul de la courbure d'un dôme.
Bonjour,
Je me tire les cheveux depuis quelques jours sur un problème purement mathématique.
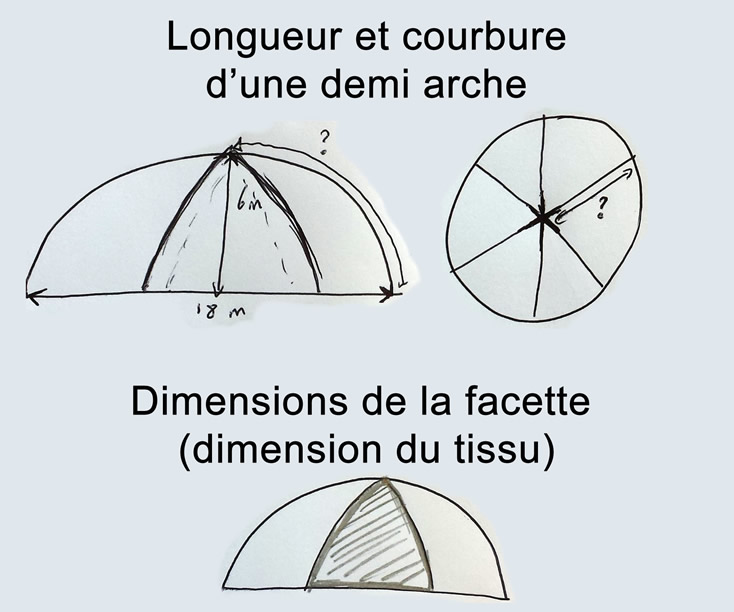
Un client me demande de concevoir un dôme de 18m de diamètre pour 6m de hauteur.
Le dôme est basé sur une structure en tube ce qui donne 6 facettes a ce dôme.
Je cherche à connaitre la longueur d'une demi arche ainsi que sa courbure.
Dans un second temps je dois équiper chaque facette d'un tissu qui prendra la courbe de l'arche.
Ma seconde question est de connaitre les dimensions et la surface d'une facette.
Je tourne en rond avec ces informations depuis quelques temps sans trouver de solutions.
Je joins un dessin expliquant la situation.
Je m'en remet a la communauté dans l'espoir que vous puissiez m'aider.
Je vous remercie par avance.
Bonjour ,
Il faudrait préciser le type de courbure souhaité (sphèrique , parabolique , elliptique ...) .
Cordialement
Merci de votre réponse,
Dans l'idée ce serait une section de sphère.
Je ne sais pas comment expliquer plus précisément.
Cordialement
Ce cas est le plus simple à résoudre puisqu'il suffit de déterminer des angles et des arcs de cercle .
Merci beaucoup pour votre réponse,
Vous me sauvez la vie 
Mes années trigo sont assez loin.
Merci d'avoir pris le temps de me répondre.
Bonjour,
Il me semble que tu as besoin aussi de la surface
Ta sphère est de rayon 9.75 m
la formule est avec h=6 et R=9.75 ce qui donne
en divisant par 6 cela donne approximativement 61.26
mais ton tissus ne va pas épouser la surface de la sphère car même avec un parasol qui possède 8 baleines
la toile est tendue entree 2 baleines consécutives.
Tu auras donc pour chaque morceau de toile un triangle isocèle curviligne de base rectiligne de longueur A'C= (le sixième de
) dont les autre côtés SC mesureront 11.466 d'après la réponse de fm_31.
tu devra évaluer les écarts à chaque niveau
Merci de ta réponse,
quelque chose m'échappe.
tu me parle d'un rayon de 9.75m... mais le diamètre de mon dôme est de 18m ça devrais faire 9m de rayon non ?
la hauteur est bien de 6 mètres en effet.
quelles mesures dois-je fournir à mon vendeur de tissu pour qu'il corresponde aux "quartiers".
J'avoue avoir du mal à m'y remettre
Comme l'a précisé DOMOREA , il n'est pas possible de mettre à plat une partie de sphère .
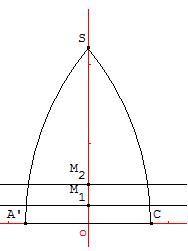
Cependant on peut faire une approximation comme sur le schéma joint (qui ne tiens pas compte des coutures) .
Avec des logiciels comme GeoGebra par exemple , on peut multiplier facilement le nombre de points intermédiaires si on souhaite plus de "précision" dans cette approximation .
Je comprend le raisonnement,
seulement je ne parviens pas a trouver les valeurs intermédiaires ( du moins la formule ) pour obtenir les valeurs comme 2.83 ...
J'essaye plein de choses avec géogebra sans résultats.
Je comprend très bien le 9.43 pour l'arc, ainsi que le 11,47 de rayon tout comme je comprend l'angle de 30°.
d'après le schéma, cela voudrait dire que [BS] est plus grand que 11,47 ?
Effectivement l'arc BS est un peu plus grand que 11,43 .
Il est obtenu en traçant le cercle dont le centre est à l'intersection de la perpendiculaire à SM et de médiatrice de SB . Ce point étant assez éloigné de S (50m) , il n'est donc pas facilement utilisable pour un tracé direct sur le tissus .
Mais avec GeoGebra , on peut le tracer facilement et relever graphiquement (sans calcul) les valeurs 1,51 , 2,83 et 3,94 (en réalité 1,54 , 2,85 et 3,95) qui vont permettre de tracer la découpe .
Si nécessaire on peut relever graphiquement d'autres valeurs en subdivisant le rayon SN en davantage de parties .
Merci beaucoup pour vos réponses,
J'ai pu reproduire le dessin et créer un point mobile sur ma hauteur me permettant d'afficher l'écart en tout point.
Vraiment top.
Merci beaucoup de ce coup main.
Bonjour,
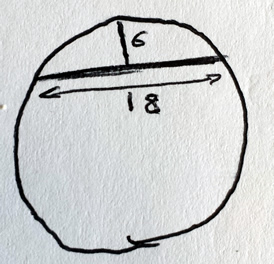
J'ai lu avec intérêt ce post car je veux recouvrir d'un toile une demi sphère de 18 cm. Mon niveau de math étant ce qu'il est, c'est à dire très bas, me permet de comprendre le principe, mais je suis totalement incapable ni de comprendre , ni à fortiori de faire ces calculs moi même.
je sais que c'est ancien, mais si vous aviez encore la méthode utilisée cela me sauverai. voilà & mois que je cherche et je commence à craquer!
merci d'avance
Pascal
Bonjour ,
comme il a été dit , on ne peut pas recouvrir une demi sphère avec une toile .
On procède donc par des approximations qu'on peut peut comparer aux fuseaux horaires de la terre . Plus on mettra de fuseaux , plus l'approximation sera fine .
Il faut donc établir le patron d'un fuseau . Pour cela , le mieux est d'utiliser des logiciels comme GeoGebra par exemple .
Cordialement
Merci du retour. j'ai bien compris le principe du quartier et j'ai fait des essais en ce sens avec des système en degrés, donc rien de suffisamment précis. quand à GeoGebra j'y suis allé mais je sais même pas par ou commencer!
Pour t'aider plus efficacement il serait bon d'en connaitre un peu plus sur le contexte .
- Est-ce un devoir de math à rendre ? Alors il faut développer les formules utilisées et les calculs faits . Quel est l'énoncé ?
- Est-ce une construction géométrique à proposer ?
- Est-ce une réalisation réelle à faire ?
- Le nombre de fuseaux est-il donné ?
- Peut-on (doit-on) utiliser un logiciel graphique ?
- .....
Cordialement
bonjour,
Il s'agit de la construction d'une maquette animée. Une demi sphère de 18 cm de diamètre doit être recouverte par de la toile de peintre pour pourvoir être peinte ensuite.
le nombre de fuseau est libre. J'ai travaillé sur la base de 8 fuseaux avec les calculs repris sur le tableau annexé et tiré d'une méthode pour faire une mappemonde. Mes calculs sont peut être faux; le report sur papier n'est pas simple non plus car impossible de le faire avec beaucoup de précision. la précision n'est pas suffisante et donc le rendu inefficace.
est-il possible de faire mieux?
j'espère que je suis clair?
merci
pascal

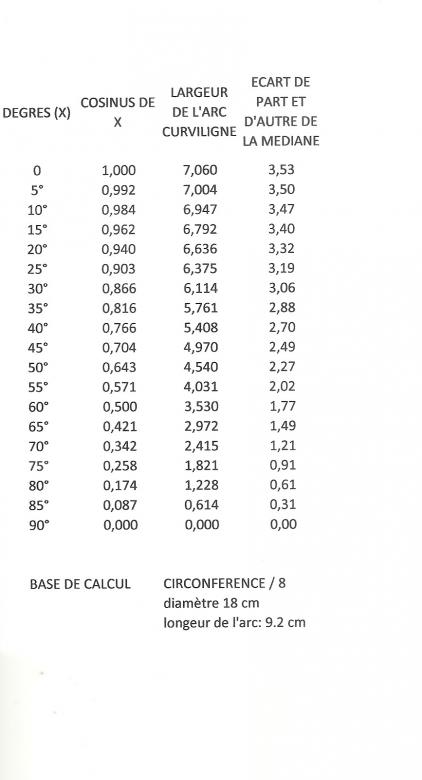
Les valeurs trouvées (largeur de l'arc curviligne*) me semblent bonnes mais pas suffisantes pour construire le patron des fuseaux .
Le mieux serait que tu m'envoies un mail (voir mon adresse dans mon profil) . Ainsi en retour je t'enverrai le fichier GeoGebra qui montre comment construire ce patron .
* un arc n'a pas de largeur mais une longueur
bonjour, je recherche de l'aide, je souhaite réaliser un dôme octogonal (tracé à partir d'un cercle de R= 8cm, la hauteur est de 3cm), comment calculer la courbe des 8 cotés me permettant de monter le dôme ? l'idéal pour moi serait de pouvoir dessiner les 8 cotés au compas
Bonjour
oui je dessin c'est bien cela, sauf que j'ai oublié de dire que les 8 cotés vont reposer sur un octogone de R2 (hauteur 3cm), qui sera positionner au centre de l'octogone principal, autrement dit , les cotés deviennent des trapèzes, dont la grande longueur sera à 6,12 (via sin 22,5 X8X2) et la petite longueur sera à 1,53 cm, mes inconnus sont la courbe du trapèze et sa hauteur
j'espère avoir été claire, merci d'avance
Ce serait plus clair si tu joignais un schéma .
Ce que je ne comprends pas entre autre :
"octogone de R2 (hauteur 3cm)"
"courbe du trapèze"
6,12 (via sin 22,5 X8X2)
merci pour votre réponse, ci-joint un schéma, ma problématique est de trouver la courbe (pente) de chaque trapèze
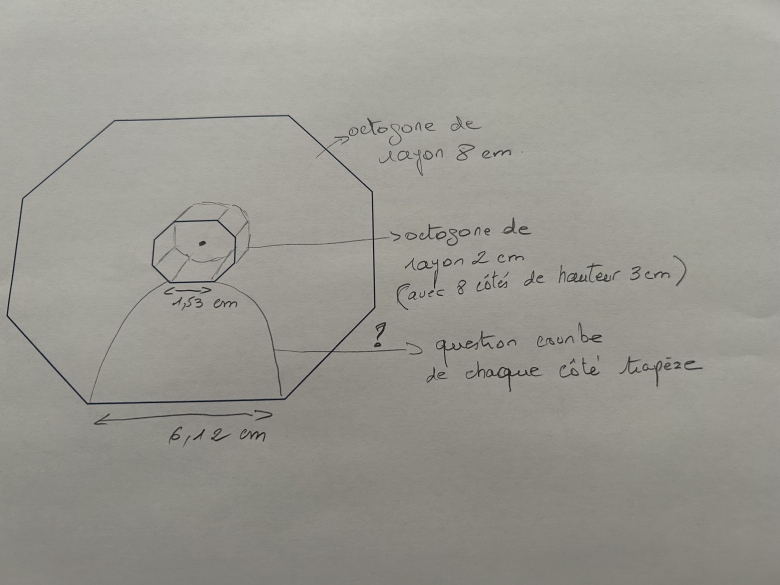
Bonsoir ,
Si ça s'éclaircit un peu , j'ai toujours quelques interrogations.
Ce que je ne comprends toujours pas est courbe de chaque côté du trapèze . Les côtés d'un trapèze sont des segments de droites , pas des courbes.
J'ai du mal à comprendre aussi ce que tu veux dire par trouver la courbe (pente). La courbe de quoi ? , la pente de quoi ?
Sur ton schéma , le dôme n'apparait pas clairement et tu ne me dis pas si mon 2° schéma est représentatif ou pas.
A moins que ce ne soit comme sur le schéma ci après ?
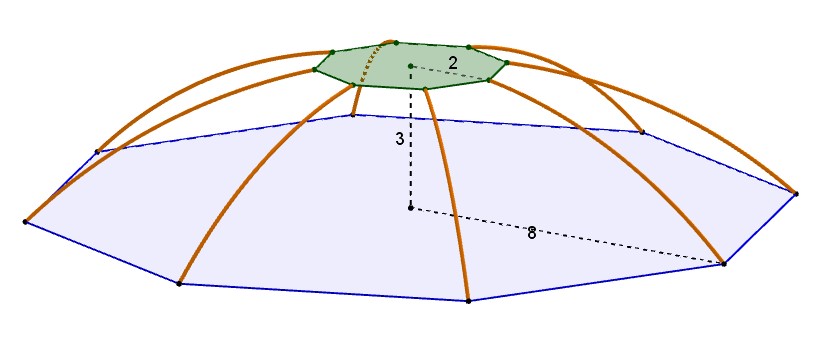
Bonjour, ton dernier schéma représente parfaitement ce que je veux faire ! un dôme c'est bien arrondi, il y a une courbure, je m'explique : les 8 trapèzes qui vont relier le grand octogone au petit octogone sont forcément courbés (il me semble), ma question est = comment les dessiner, quelles sont les mesures ? voir mon schéma (en fait le tien) dans lequel j'ai indiqué ma recherche, point c que je voudrais dessiner avec un compas
Encore merci
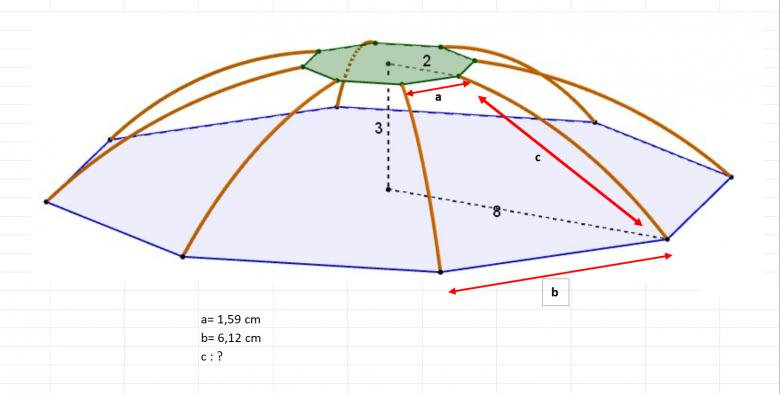
Bonjour,
Avec un compas, tu n'y arriveras pas (sauf à faire de l'approximatif). Mais la résolution exacte fait intervenir une fonction spéciale, une intégrale elliptique. Tout d'abord un petit schéma, plus sommaire que celui de fm_31, repésentant un pan du dôme vu de dessus et vu de profil . Ensuite, je fais des calculs au moyen du logiciel de calcul formel Maple. D'abord, je rentre la paramétrisation de l'armature droite du pan de dôme. C'est un arc de cercle de rayon 7,5cm.
M:=[sin(Pi/8)*(2+15/2*s), -cos(Pi/8)*(2+15/2*s), -9/2+15/2*sqrt(1-s^2)];Le paramètre
Je calcule ensuite en fonction de
:
N:=simplify(sqrt(diff(M[2],s)^2+diff(M[3],s)^2),trig);
L:=int(N,s);
L'expression de la longueur d'arc d'ellipse est une véritable horreur:
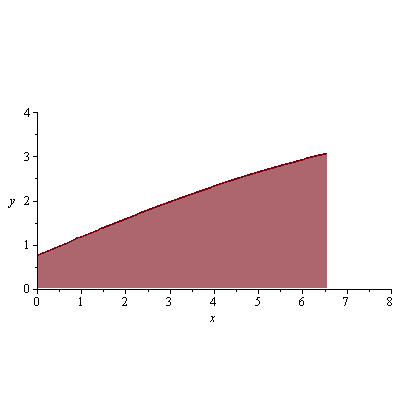
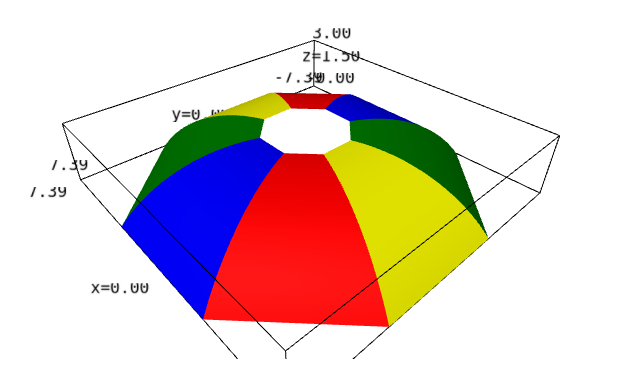
Tu vois que le compas est hors-jeu. Mais ça n'empêche pas de faire dessiner le demi-pan de dôme mis à plat :
plot([L,M[1],s=0..4/5],x=0..8, y=0..4,filled=true, scaling=constrained);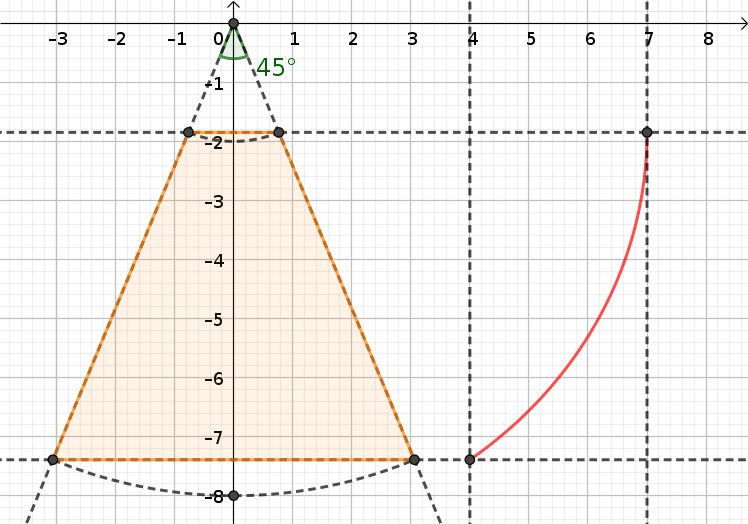
Bonsoir à tous.
Avec une interprétation plus simple que celle de GBZM : je considère que la figure est tracée sur une sphère que l'on voit en coupe ci-dessous.
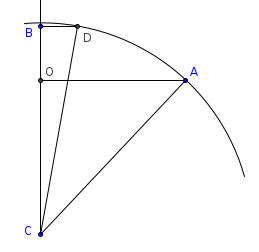
Par hypothèse on a OA=8, OB=3 et BD=2.
Soit C le centre du cercle on a
(OC+OB)2+BD2=OC2+OA2
on en déduit facilement OC=17/2, puis le rayon AC du cercle.
Pour la longueur de l'arc AD
on calcule l'angle ACD=arctan(16/17)-arctan(4/23).
L'interprétation n'est pas plus simple, elle est différente.
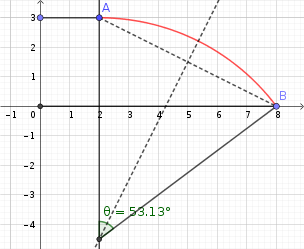
J'ai mené mon calcul avec l'armature circulaire arrivant horizontale au sommet de l'octogone du haut. Ça donne le dessin en bas du message, et un arc de cercle de rayon 15/2. L'angle est
car on voit dans la figure un triangle rectangle de côtés dans la proportion 3, 4, 5. La longueur de l'arc de cercle formant l'armature est donc
.
So far so good, mais ce que semble oublier verdurin est que l'arc de cercle formant armature n'est pas, dans un cas comme dans l'autre, le profil du pan de dôme ! Le profil du pan de dôme est la projection de cet arc de cercle sur le plan médiateur de deux sommets consécutifs de l'octogone, et cette projection est une ellipse. La longueur d'un arc d'ellipse, c'est plus coton !
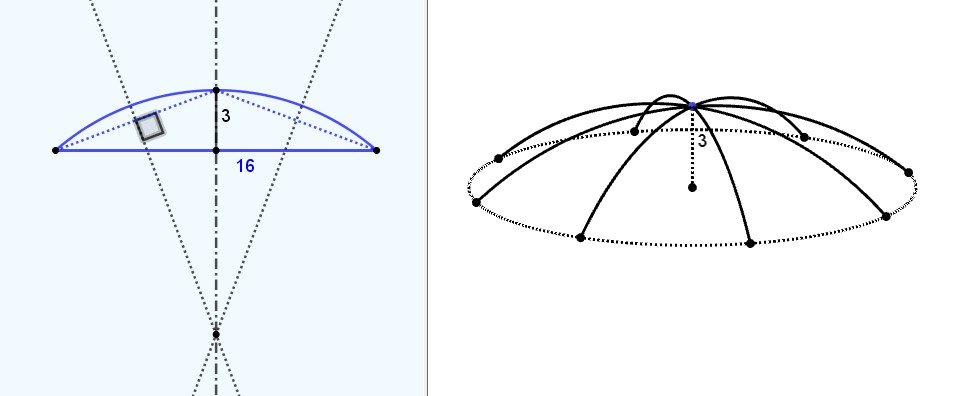
Maintenant qu'on est enfin clair sur le schéma , un certain nombre d'éléments peuvent être déterminés. Voir ci après. Est-ce que ça répond à tes attentes ?
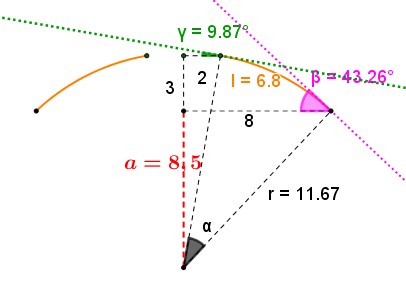
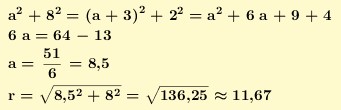
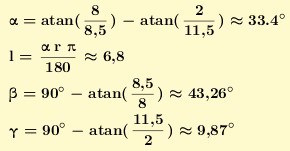
Maintenant qu'on est enfin clair sur le schéma
Pas tout à fait, comme je l'ai expliqué dans mon message précédent.
Tu considères comme verdurin que les armatures sont des arcs de cercle dont le centre est situé sur l'axe du dôme. Ces arcs de cercle n'arrivent donc pas horizontalement au sommet du petit octogone supérieur.
Je considère au contraire que les armatures sont des arcs de cercle qui arrivent horizontalement au sommet de l'octogone supérieur.
À Kino83 de préciser ce point.
Par ailleurs il me semblait comprendre que Kino83 voulait savoir la forme des courbes qui sont les côtés du trapèze curviligne plan qui est un pan de dôme tendu entre deux armatures, une fois mis à plat. En gros, avoir un patron pour découper dans du tissu un pan de dôme qu'il fixera sur les armatures en arc de cercle entre l'octogone du bas et celui du haut. Me trompé-je ? Encore un point sur lequel Kino83 devrait préciser sa demande.
De toutes façons on ne peut pas « aplatir » une sphère, ni même une portion de sphère.
En d'autre termes, je dis ça pour Kino83, il est impossible d'avoir un morceau de de plan qui se place entre deux armatures pour faire une portion de sphère.
On peut bien sur mouler un tissu ou un papier humide et encollé pour que ça marche à peu près.
Ma chérie l'a déjà fait, mais ça ne relève pas des mathématiques. C'est de l'artisanat.
Bien sûr qu'on ne peut pas aplatir une sphère, et je n'ai jamais parlé de morceaux de sphères. Les pans du dôme que je calcule et qui s'attachent sur les armatures en arcs de cercle sont des morceaux de cylindre qui s'aplatissent parfaitement en un trapèze avec côtés curvilignes. Déterminer la forme des côtés relève tout à fait des mathématiques.

J'ai inutilement compliqué l'expression de la longueur de l'arc d'ellipse en travaillant avec plutôt qu'avec
, l'angle au centre de l'arc de cercle sur l'armature. Avec
, c'est simplement
Beaucoup plus sympathique, mais toujours avec une intégrale elliptique de seconde espèce.
Merci à tous pour vos réponses détaillées ! j'ai testé la proposition de FM31 (r = 11,67), c'est quasi parfait, mais il reste encore des espaces vides, il me semble que j'ai oublié de préciser une donnée importante, la hauteur du trapèze (6,7cm), merci à tous
Tiens, un revenant !
Des questions : est-ce que tes pans de dôme (tes "trapèzes") sont une fois en place des morceaux de cylindre s'appuyant sur des armatures en arcs de cercles (les "arêtes" du dôme) ?
Est-ce que ces armatures en arcs de cercles arrivent horizontalement à l'octogone du haut ? Ou est-ce que ce sont des arcs de cercle dont le centre est sur l'axe du dôme ?



 trigonométrie en post-bac
trigonométrie en post-bac