Inscription / Connexion Nouveau Sujet
calcul de poids
Bonjour,
J'ai de nouveau de la difficulté à faire un exercice que voici :
1)
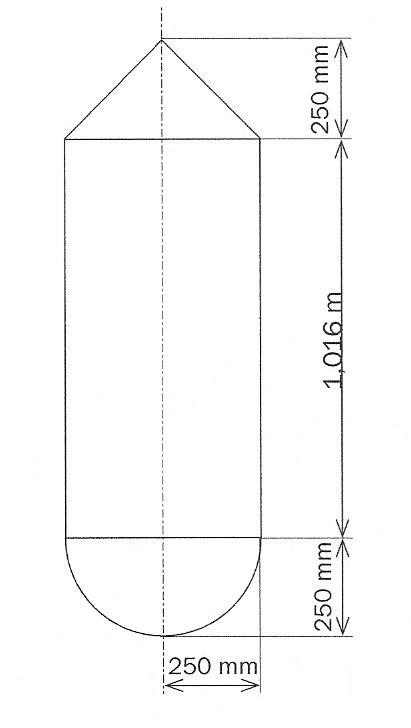
Trouvez le poids du récipient vide représenté par la figure ci-contre. Il est en acier de 5mm. Le poids du métal est 8kg au m² par mm d'épaisseur.
2)
Trouvez le poids total du récipient, rempli aux trois quarts de la partie cylindrique d'un liquide de densité 0.907.
Je connais la formule pour calculer le poids qui est :
P(kg) = densité × Volume (dm^3)
Il faut, je pense et dans un premier temps, calculer les volumes du cylindre, du cône et de la sphère avec les formules :
V(cylindre)=πR² h
V(sphère)=4/3 πR^3
V(cône)=1/3 πR² h
Puis les additionner pour avoir le volume total ...
Seulement voila, avec toutes ces unités différentes comment procéder ? Faut il préalablement tout convertir ? J'ai essayée en mm, je me retrouve avec des chiffres énorme 
Quelqu'un pour me mettre sur la voix ???
C'est plus compliqué que ça. C'est la surface extérieure que tu cherches, pas le volume. C'est un récipient, il n'est pas plein !
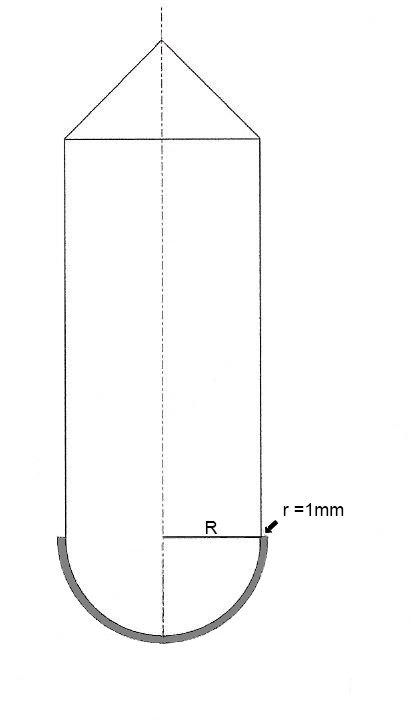
Il faut sommer les surfaces pour 5 rayons différents, correspondant à 5 couches de 1 millimètre. Si tu veux faire le calcul précis il va falloir savoir de combien sont espacés lesdites couches et si les mesures données correspondent à la couche interne ou à la couche externe.
L'autre solution, c'est de calculer la différence entre le volume pour le rayon R et le volume pour le rayon R+h, avec h = 5mm. Ou bien avec le rayon R-h. Ca ne fera pas une grande différence vu les dimensions du récipient
Ci-dessous un schéma pour la première couche.
Juste pour la cuve en demi-sphère, ca fera un volume
. Tu peux faire pareil avec le cylindre et le cône ensuite et en déduire le poids de la première couche de métal, entre R = r+r.
Ensuite, il y a une deuxième couche, d'épaisseur , qui se trouve à une distance
de la première couche, c'est à dire entre les rayons
et
. Même méthode, mêmes calculs.
Et ensuite la troisème couche à une distance de la deuxième, une quatrième à distance
de la troisième, et une cinquième à distance
de la quatrième.
En fonction de comment tu modélises la chose, tu peux décider que les couches sont collées les unes aux autres (tous les ), ou que toutes les couches ont une épaisseur de 1mm (tous les
). C'est toi qui vois

salut
je ne comprends pas trop ces histoires de couche ni cette histoire de en rouge
Il est en acier de 5mm. Le poids du métal est 8kg au m² par mm d'épaisseur.
Quelqu'un pour me mettre sur la voix ??? je peux évidemment le crier ... mais j'ai bien peur que tu n'entendes rien !!!

pour moi la couche d'acier me semble homogène avec pour masse tout simplement 8 kg par mm3 ...
ainsi il me semble que la demi-sphère d'épaisseur 5 mm à tout simplement pour volume la différence des volumes des boules de rayon r + 5 et de rayon r ...
et on fait de même pour les parties cylindrique et conique ...
bonjour
carpediem
c'est 8 kg par mètre carré sur 1 mm d'épaisseur...
tetelle62490
vu les dimensions le mieux me semble de travailler en dm pour les distances, dm² pour les aires et dm3 pour les volumes.
1 m²  1 mm = 100 dm²
1 mm = 100 dm²  0,01 dm = 1 dm3
0,01 dm = 1 dm3
donc ton métal fait 8 kg/dm3
ensuite faut calculer les volumes de toutes tes parois... je présume que les dimensions sont "externes"
vu la précision des données, je pense qu'il est raisonnable d'arrondir les calculs de volume au mm3 près, donc 6 décimales pour les volumes en dm3
le cylindre :
son volume est la différence entre la volume du cylindre externe moins le volume du cylindre interne
ha oui damned !!! ça fait un peu lourd sinon !!!
merci matheuxmatou pour ta vigilance 
sinon je vois que tu es d'accord avec ce que je propose ...
certes, mais tetelle62490 est en reprise d'étude ingénierie, donc je pense qu'il travaillent plutôt en valeurs approchées.
d'ailleurs l'énoncé ne donne aucune consigne sur la précision attendue pour les masses finales... le gramme ? le milligrammes ?
Bonjour à tous,
Merci pour vos réponses 
Les enfants étant à l'école, je vais pouvoir me remettre à travailler sur le sujet 
donc j'ai :
V(sphère) = (4/3 × π × 2.53 ) - (4/3 × π ×2.453 ) = 4/3 × π × 0.918875 ≈ 3.848974 dm3
V(cône) = (1/3 × π × 2.5² × 2.5) - (1/3 × π × 2.45² × 2.5) = 1/3 × π × 0.61875 ≈ 0.647953 dm3
D'où :
V = V(cylindre) + V(sphère) + V(cône) = 7.899849 + 3.848974 + 0.647953 = 12.396776 dm3
Et par conséquent :
P = 8 × 12.396776 = 99.174208 kg

dm
le cône "intérieur" ne fait pas 2,5 dm de haut ...
Je ne comprend pas, pour quel raison ? La mesure donnée est bien 250mm donc 2.5

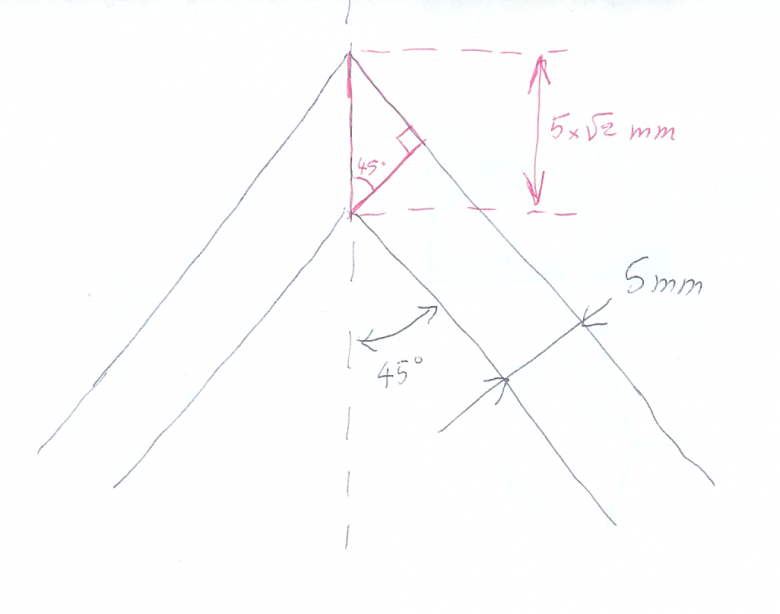
le cône extérieur fait bien 2,5 dm de haut... mais pas le cône intérieur
fais un dessin des 2 cônes emboités l'un dans l'autre...
non !
l'épaisseur de la tôle est 5 mm mais à la pointe la différence de hauter est plus grande que 5 mm
fais un dessin coté
ah oui d'accord je comprends un peu mieux !
Mais du coup, comment je peux calculer cette différence d'épaisseur ?
ok donc 5√2 ≈ 7.1 mm → 0.71 dm
Et : h = 2.5 - 0.71 = 1.79 dm
D'où:
V(cône) = (1/3 × π × 2.5² × 2.5) - (1/3 × π × 2.45² × 1.79) = 1/3 × π × 4.880525 ≈ 5.110874 dm3
Par contre après réflexion c'est une demi sphère et non une sphère donc la formule est bien :
V(demi-sphère) = (4/6 × π × 2.53 ) - (4/6 × π × 2.453 ) = 4/6 × π × 0.918875 ≈ 1.924487 dm3
D'accord merci 
Donc finalement j'ai :
V(cône) = (1/3 × π × 2.5² × 2.5) - (1/3 × π × 2.45² × 1.79) = 1/3 × π × 4.880 ≈ 5.11 dm3
V(cylindre) = (π × 2.5² × 10.16) - (π × 2.45² × 10.16) = π × 2.5146 ≈ 7.90 dm3
V(demi sphère) = (4/6 × π × 2.53) - (4/6 × π × 2.453) = 4/6 × π × 0.918875 ≈ 1.92 dm3
D'où :
V = V(cylindre)+V(demi sphère)+V(cône) = 7.90 + 1.92 + 5.11 = 14.93 dm3
Et par conséquent :
P = d × V = 8 × 14.93 = 119.44 kg
Ensuite pour le 2):
On sait que : R(intérieur)=2.5 dm ; h(cylindre)=10.16 dm
Pour la partie cylindrique, on a :
h(liquide) = 3/4 × 10.16 = 7.62 dm
V(liquide) = π × 2.45² × 7.62 = 143.69 dm3
Pour la partie sphérique :
V(liquide) = ( 4/6 × π × 2.453 ) = 30.80 dm3
Donc :
V(liquide demi sphère+liquide cylindre) = 143.69 + 30.80 = 174.49 dm3
D'où :
P= 119.44 + (0.907×174.49) ≈ 119.44 + 158.26 ≈ 277.7 kg
quand on fait les calculs sans arrondir... ou seulement à la fin arrondir au gramme on trouve
P(récipient vide)  119,482 kg
119,482 kg
P(récipient rempli)  277,748 kg
277,748 kg
c'est très bien 
Super ! 
Merci beaucoup pour toutes les explications et pour l'aide !
Encore une fois, ce forum est vraiment top 
Bonjour,
Il me semble qu'une petite erreur se soit glissée.
ok donc 5√2 ≈ 7.1 mm → 0.71 dm Faux. C'est 0,071 dm
Et : h = 2.5 - 0.71 = 1.79 dm et donc faux également
D'où:
V(cône) = (1/3 × π × 2.5² × 2.5) - (1/3 × π × 2.45² × 1.79) = 1/3 × π × 4.880525 ≈ 5.110874 dm3 faux
ah ben oui tiens ! j'avais même pas vérifié !!!! j'avais repris ses résultats sur le principe sans me pencher sur les calculs intermédiaires... 
merci alma78 
d'où
P(récipient vide)  87,334 kg si je ne m'abuse
87,334 kg si je ne m'abuse
Effectivement, petite erreur d'inattention de ma part 
Et donc après reprise des calculs je retrouve bien les mêmes résultats que matheuxmathou 
Merci alma78 
(va falloir que je nettoie mes lunettes ! heureusement qu'il y en a des plus vigilants
 )
)Je vais penser à nettoyer les miennes aussi !

Ce qui m'a interpellé c'est que tetelle62490 trouvait un cône qui faisait 5 litres (à la grosse) alors que la demi-sphère faisait 2 litres. Alors que à l'œil, ce n'est pas du tout ça.


 en post-bac
en post-bac