PS 3 : mais qu'est ce qu'il est petit surtout ! Je suis très déçu.

Au lieu de croire : regarde par exemple


http://www.math.univ-toulouse.fr/~raymond/book-CD-LIM.pdf
..

Oui merci, j'ai eu largement le temps de vérifier entre temps.

Je l'ai laissé en PS parce que je supposais que c'était à partir de là qu'il fallait partir dans la résolution de l'exercice.

Comme je l'ai dit, je n'ai pas trop de problème avec la définition, mais plus dans son application : on la trouve comment cette fonction linéaire qui satisfasse la définition de la GDérivée ?

PS : je connaissais déjà le poly, j'en ai épluché une dizaine mais cela ne m'a pas servi pour l'instant.

As-tu calculé les dérivées directionnelles de  } à l'origine ? (tu remarqueras qu'un petit d peut avoir des effets grossissants). Il convient de distinguer les cas et pour faire les calcul dans la direction (x_1,x_2).
Peux-tu en déduire la différentielle au sens de Gâteaux à l'origine ? (C'est facile !). C'est une forme linéaire très, très simple.
Pour vérifier ensuite si la fonction donnée est différentiable au sens ordinaire à l'origine, on regarde (puisque ) si tend bien vers 0 quand tend vers . C'est bien sûr le cas si on suit une direction donnée, mais ça ne suffit pas...

Au fait : avoir des dérivées partielles en (0,0), ça ne veut pas dire avoir des dérivées dans toutes les directions en (0,0), et encore moins être Gâteaux différentiable.

Hello GaBuZoMeu, merci de t'occuper de mon cas ! (J'ai l'impression d'être aux urgences)

1) Gâteaux-différentielle

Citation :
As-tu calculé les dérivées directionnelles de   à l'origine ?

Citation :

1° Ca ne va pas. La dérivée directionnelle associée au vecteur à l'origine est . Relis tes définitions !

2° Dire que est différentiable à l'origine avec différentielle la forme linéaire , c'est dire que
autrement dit, puisque , que

1) Gâteau-Différentielle (suite et fin ?)

Citation :
1° Ca ne va pas. La dérivée directionnelle associée au vecteur à l'origine est . Relis tes définitions !

Est-ce que tu as divisé par N₂ (x₁,x₂) des deux côtés, ce qui nous donne O(1) qui est égal à 0 ?
Je suis pas terrible en négligence d'une fonction, j'ai un peu séché le cours dessus.

1) " le quotient est équivalent en 0 à t⁴/t³ fois une certaine constante"
Non. En particulier si (ou comme tu préfères) est nul, ce n'est sûrement pas vrai.
2) "j'ai un peu séché le cours dessus"
Nul ne peut se prévaloir de ses propres turpitudes.

Ok je vois que tu es pointilleux, je n'ai pas cherché à différencier les cas d₁ ou d₂ 0. (On ne le fait pas en cours, c'est pour cela que je n'ai pas pensé à le faire.

1) Gâteau-Différentielle

- Si d₂=0 et d₁=0, on a que toute fonction est dérivable selon la direction nulle, donc c'est bon.

- Si d₂=0 et d₁0, cela ne change pas grand-chose (car d₂ ne factorise ni le dénominateur ni le numérateur), et on a bien l'équivalence avec le quotient t⁴/t³ qui tend vers 0 quand t tend vers 0.

- En revanche, si d₁=0 et d₂0, cela peut poser un problème, car au numérateur, on aurait
On voit donc bien pourquoi le cas d₂=0 ne pose pas problème, mais le cas d₁=0 si.

Cependant, je n'arrive pas à savoir comment résoudre ce contre-temps. Il faut réussir à simplifier les d₁ pour que le numérateur ne soit plus facteur de d₁ ?

2) Fréchet-Différentielle

Soit. Je ne sais pas pourquoi on prend la norme N₂ systématiquement (parce que c'est celle qui nous arrange ?). Donc dire que f est (Fréchet-)dérivable par prolongement en (0,0), c'est dire que :


C'est ça ?

Il faut donc prouver, puisque la norme et f sont positives, que le quotient est strictement supérieur à 0, puisqu'on nous demande de prouver qu'elle n'est pas (Fréchet-)dérivable.

Encore une fois, j'ai la correction (prouver l'appartenance de f à un certain cercle, puis en déduire que sur ce cercle, le quotient est égal à une certaine constante, pour tout vecteur (x₁,x₂)), mais je préfère me faire guider pour y parvenir, pour comprendre définitivement.

3) Question subsidiaire (tu n'es pas obligé d'y répondre si ça te gave)

Clairement, est-ce qu'une fois qu'on a réécrit la condition pour que la fonction soit Fréchet-Dérivable, existe-t-il une astuce ou une démarche à suivre pour savoir si elle l'est ? Et comment le démontrer ensuite ?


Merci en tout cas !

Tu trouves qu'éviter d'écrire des choises fausses c'est être pointilleux ? Alors oui, je suis pointilleux.

Pour le cas , prend un peu de recul sur ce que tu écris, et réfléchis !

Toutes les normes sur un espace de dimension finie sont équivalentes. On prend celle qui nous arrange.

"Il faut donc prouver, puisque la norme et f sont positives, que le quotient est strictement supérieur à 0".
Je vais être encore pointilleux : ce que tu écris là ne va pas.

1) Est-ce que 0 tend vers 0 ? Grave question !

2) Ca ne va toujours pas. Une quantité strictement positive ne peut pas tendre vers 0, selon toi ?

1) Je suis.. pointilleux
Sérieusement, c'est plus facile de douter de tout quand on bute sur la compréhension d'un exo.. Je me suis même demandé toute à l'heure si un carré était forcément positif, c'est te dire. (Je plaisante hein).

2) Si. Bon donc il faut prouver tout simplement que cette quantité ne tend pas vers 0 lorsque le vecteur x tend vers 0. COMMENT FAIT-ON ?

Je ne sais pas si tu as déjà répondu, mais si non, j'ai peut-être débusqué une piste, je la poste dès que je parviens à quelque chose.

Bon, pas terrible ma piste, peut-être que je n'arrive pas à conclure.

Je pars du quotient . L(x₁,₂) est nulle, c'est la GDérivée/GDifférentielle.

En fait, j'ai essayé de chercher pour quelles valeurs du vecteur x le quotient était strictement positif, pour voir s'il était nécessairement strictement positif, même lorsque x tend vers 0, mais non seulement j'obtiens qu'il est strictement positif si x₁ est strictement non nul, mais en plus ça revient à faire ce que j'ai proposé au début, donc c'est FAUX.

Toute aide de ta part sera donc appréciée
Merci.

Le fait que f soit dérivable à l'origine dans chaque direction montre que que tend vers 0 quand tend vers l'origine selon une droite. On peut donc essayer de trouver une courbe, pas droite, arrivant à l"origine et le long de laquelle ce quotient ne tend pas vers 0. Tiens au fait, ce quotient, tu peux l'écrire explicitement pour qu'on y voie plus clair ?

Ca me semble assez visuel non ? Si un point (x_1,x_2)

Ca me semble assez visuel non ? Si un point tend vers l'origine, il peut y aller tout droit ou en tournant. Ca ne te parle pas ?

Si, visuellement je me le représente assez bien dans repère à 3 dimensions.
C'est la transcription "analytique" que je n'arrive pas à faire, mais je crois que je commence à comprendre.

Quand on est dans un repère à 2 dimensions, càd une fonction qui associe un réel quelconque à un réel, par exemple, x ne peut tendre vers 0 "qu'en y allant tout droit", et en l'occurrence en suivant la droite passant par x et l'origine.

Quand on est dans un repère à 3 dimensions, càd une fonction qui associe un vecteur de ² à un réel, on a la possibilité de faire suivre au vecteur x une courbe pour le faire atteindre 0_².

Pour m'aider à comprendre comment on écrit tout ça en terme de fonction, j'ai quelques petites questions :
- L'équation de la courbe doit nécessairement coïncider avec le graphe de f non ?
- Comment trouve-t-on l'équation de la courbe qui satisfasse notre problème ?

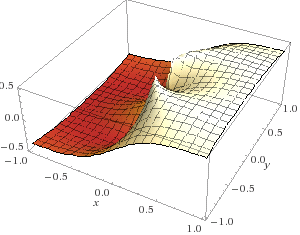
J'ai joint à mon poste le graphe de la fonction sur [0,1]².

Le graphe de la fonction f que l'on étudie.

Je ne comprends rien à ton histoire de 2 et 3 dimensions. La droite et la courbe sont bien sûr tous les deux dans le plan.
Pour ne pas trop traîner, je te vends la mèche : regarde ce qui se passe quant on suit la courbe (avec t tendant vers 0, bien sûr). On peut deviner que c'est un bon choix en contemplant le graphe.

Hello GaBuZoMeu !

Tout d'abord je m'excuse de mon absence, j'ai du acheter un nouveau chargeur d'ordinateur car l'ancien m'avait lâché (donc plus d'ordinateur pendant quelques jours). Je te remercie encore une fois de m'aider ( & de ta patience ).

Malheureusement, mon absence est peut-être autant virtuelle qu'intellectuelle : je pense que je vois où tu veux en venir, j'ai saisi que l'on voulait faire tendre notre quotient vers un nombre différent de 0 en faisant suivre à la fonction f une trajectoire en forme de courbe, mais tu me demandes malheureusement de répondre à la partie de l'exercice où je n'ai rien compris.

Je n'arrive pas à expliciter cela. Et pourtant la correction de mon exercice semble me proposer quelque chose de similaire à ta correction, mais je ne vois pas comment l'écrire (comment trouver une courbe adéquate ? comment en conclure que le quotient ne tend pas vers 0 lorsque le vecteur x tend vers l'origine ?).

Donc premièrement : ça veut dire quoi une courbe de paramètre x₁(t) et x₂(t) ? J'ai regardé dans mon cours, et je n'en ai pas d'exemple.. (On a seulement étudié les équations cartésiennes d'une courbe et je t'avoue que je ne vois pas comment la trouver via tes indications..).

"ça veut dire quoi une courbe de paramètre et ?"
Ca ne veut rien dire, et ce n'est pas ce que j'ai écrit.
Tu n'as jamais vu de courbe paramétrée de ta vie ?
La courbe , par exemple, ça ne te dit rien du tout ?
Ici, quand je te suggères de regarder ce qui se passe quand on tend vers 0 en suivant la courbe , il suffit de remplacer dans l'expression de la fonction les coordonnées et par et respectivement, et de chercher la limite de cette fonction de quand tend vers 0.

Je l'avais fait au cas où..

Et je ne trouvais rien de probant.. Même pour le quotient.

Je me retrouve (en remplaçant respectivement dans la fonction et dans le FAMEUX quotient) :






Quand t tend vers 0, les deux quotients tendent irrémédiablement vers 0 non ?

1°) Ne pas reconnaître dans (cos(t),sin(t)) une paramétrisation du cercle unité, faut le faire. Tu es en L2 math-info, tu n'as pas fait que de l'optimisation, je suppose ? Peut-être as-tu aussi séché les cours sur les courbes paramétrées ?
2°) Tu t'es trompé en recopiant f. Reprends les choses plus soigneusement.

1)

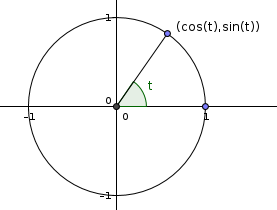
Non, vraiment rien ?

Les bras m'en tombent...
Arriver en deuxième année d'études universitaires en maths et n'avoir aucune idée de ce qu'est une courbe paramétrée. Si vraiment tu n'as rien séché, c'est qu'il y a quelque chose qui ne tourne pas rond dans le cursus que tu as suivi.

Imagine : t, c'est le temps. Au temps t, un mobile dans le plan est donné par ses coordonnées cartésiennes (x(t), y(t)). Quand le temps s'écoule, le mobile décrit une courbe dans le plan.

Je suis sûr que ton logiciel dessine des courbes paramétrées. Voici ce que fait le mien (Sage) quand je lui demande de dessiner la courbe (t^2,t) pour t variant entre -2 et 2 :

Ah au fait : la limite ce n'est pas 1...

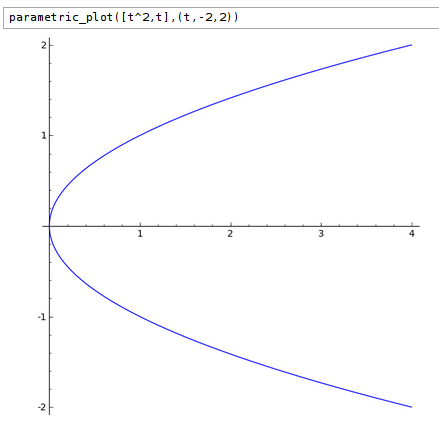
1) Réponse

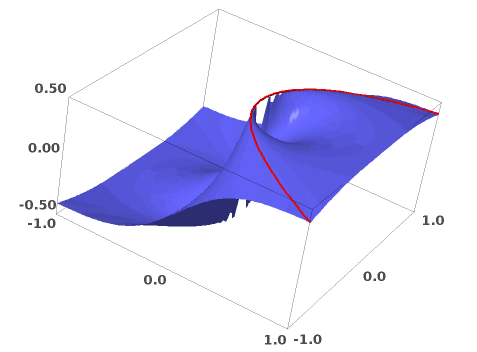
Très chouette le graphique, je visualise beaucoup mieux ! Merci !

Je vais réétudier le "rôle de x₁" comme tu dis, parce que je n'avais pas l'impression que tu voulais me faire comprendre toute la démonstration via son comportement en 0.

Mais donc d'un point de vue pragmatique, si je tombe sur un énoncé légèrement différent, cela signifie que n'ayant ni "intuition" digne de ce nom dans le domaine, ni "expérience", je vais me vautrer c'est ça ?


PS : j'ai vu que tu étais professeur, et je ne sais pas si tu connais déjà ce site (ici c'est le lien qui mène au graphe que j'ai trouvé), mais c'est un outil en ligne gratuit très puissant pour effectuer toute sorte de "recherche" dans le domaine des sciences (pas seulement les mathématiques), et qui permet notamment la représentation de fonction en 3D, notamment. Notre professeur de TD nous l'a donné et il m'a beaucoup servi, et je sais que c'est le cas des autres élèves. Voilà

Même si le but principal de ce topic était de comprendre comment parvenir à démontrer qu'une fonction n'était pas Fréchet-différentiable dans un cas général, but pour lequel il ne semble pas exister de "solution générale", je te remercie de ta patience & de tes explications, car j'ai au moins bien compris ce qu'était une Gâteau-différentielle ainsi qu'une Fréchet-différentielle et j'ai plutôt bien assimilé ces notions maintenant.

J'espère que ce topic pourra servir à d'autres personnes !

Oui, je connais le site de Wolfram. Mais je préfère utiliser sur ma machine un logiciel de calcul formel, en l'occurrence Sage qui est libre et gratuit :

Je pense que ton corrigé ne dit pas tel quel "l'appartenance de la fonction au cercle de coordonnées : .". Mais il dit peut-être que la fonction   vaut 1/2 en tout point de ce cercle. On s'en aperçoit facilement en réécrivant l'équation de ce cercle sous la forme
Quel rapport entre ce cercle et la parabole ? Ces deux courbes ont un contact d'ordre 3 à l'origine (le cercle a une paramétrisation ).

Ton résumé est incorrect : "l'intersection de f et du cercle" ne veut rien dire. Comment intersecter une fonction avec une partie du plan ? J'ai pourtant dit les choses correctement (et en une demi-ligne), pourquoi les reformules-tu incorrectement ?

Pourquoi dis-tu que le cercle et la parabole n'ont aucun rapport, alors que je viens justement d'expliquer le contraire : à savoir que le cercle est "collé" à la parabole (ou vice-versa) au voisinage de l'origine. C'est d'ailleurs pour cette raison qu'ils fournissent tous les deux une façon de tendre vers l'origine telle que la limite du quotient soit égale à 1/2 dans les deux cas.

Ton énoncé indiquait ce qu'il fallait faire, en annonçant le résultat : pas de Fréchet-différentiabilité à l'origine. Il fallait juste montrer la non-continuité du quotient à l'origine. Ce qui était un peu compliqué, c'est que le quotient tend vers 0 quand on tend vers l'origine le long de n'importe quelle droite passant par l'origine. Il fallait donc faire un peu plus rusé, et j'ai déjà dit les raisons poussant à chercher une courbe tangente à la droite .

Je te conseille de faire un effort pour employer des formulations correctes techniquement. Tu vas être évalué prochainement. Ce qui va être évalué, c'est ce qui est écrit sur ta copie, pas ce que tu as dans la tête en écrivant.

J'en suis parfaitement conscient !

J'ai remarqué, et cela est aussi vrai dans mon cas, qu'il y a moins de rigueur de sa part lorsqu'un étudiant poste sur un forum : on ne sait pas comment exprimer tous les symboles mathématiques que l'on voudrait, on a un devoir de concision qui nous fait parfois élaguer certaines données non négligeables (ce que l'on aurait pas fait en contrôle par exemple) et dans mon cas, j'ai très peu de temps à chaque fois pour poster sachant que j'ai plusieurs autres matières à travailler, ce qui peut même m'amener à écrire des erreurs alors que c'est un peu plus clair dans ma tête.

Mais il est clair que toutes les précisions que tu m'as apportées me serviront et je les réemploierai à nouveau si j'y suis confronté dans ma copie. D'autant que mon maître de conférence n'est pas connu pour son laxisme en la matière.

Je te remercie donc pour tous tes conseils et tes explications, l'essentiel c'est que je sois parvenu à comprendre (le graphique a beaucoup aidé) qu'une fonction peut ne pas être fréchet-différentielle même si le quotient impliqué semble tendre vers 0 (selon une droite).

À la prochaine !