Inscription / Connexion Nouveau Sujet
calcule de hauteur d'une pyramide à base rectangulaire
Bonjour j'aimerais savoir comment calculer la hauteur d'une pyramide à base rectangulaire ,
je sais que je peut utiliser le théorème de Pythagore donc ,
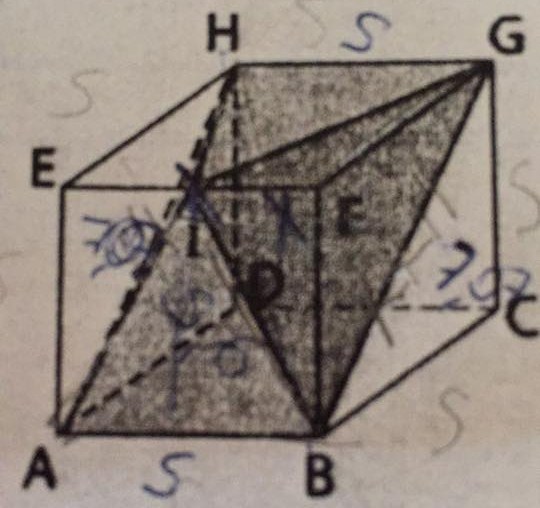
ABCDEFGH est un cube d'arête 5cm , le point I est le milieu de l'arête [EF]
on me demande de déterminer la hauteur de la pyramide IABGH issue de I , pour trouver la hauteur j'ai tracé les diagonal de la base rectangulaire se qui ma donné la hauteur et je l'ai appelé N , la hauteur est donc le segment [IN]
en suite on me demande calculer cette hauteur ,
j'ai déjà calculer a l'aide du théorème de Pythagore le côté HA = 7.07
En suite j'ai un peu de mal , merci de votre aide , est ce que vous connaissais un autre logiciel que geoplan geospace pour créer des figures dans l'espace merci
Pour y voir plus clair, je te conseille de faire une figure complémentaire représentant la coupe du cube par le plan passant par le point I et perpendiculaire au côté EF.
Bonjour,
autre logiciel que Geoplan / Geospace : Geogebra l'essayer est l'adopter à mon avis, vu l'ergonomie à ch... de Geoplan
il me semble que la dernière version fait du 3D (pas essayée)
mais ici le meilleur logiciel est encore un bout de papier et son cerveau 
un dessin à main levée sur un bout de papier fait tout aussi bien l'affaire que de "contempler" passivement des beaux dessins faits par un logiciel.
l'avantage du logiciel est ici qu'il permet d'obtenir des figures "exactes" à peu de frais et surtout "toutes propres" si on sait bien s'en servir.
mais à mon avis pour avoir exactement ce qu'on veut, il va falloir "tricher" en cachant des trucs, en créant des plans supplémentaires "de coupe" etc pour ne pas avoir des plans qui peignent toute la surface de la fenêtre inutilement, ce qui ne représente plus rien au final. Et donc bien plus de travail que le "dessin à main levée au brouillon"
ou alors utiliser le logiciel en 2D pour construire en 2D la perspective...
MERCI de votre aide je pense avoir résolut cette affaire voici ma démarche
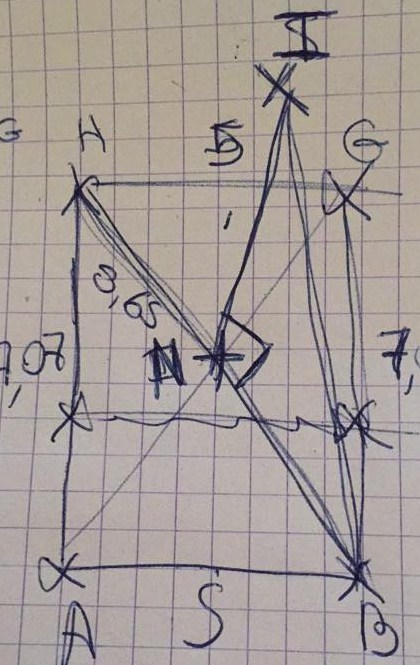
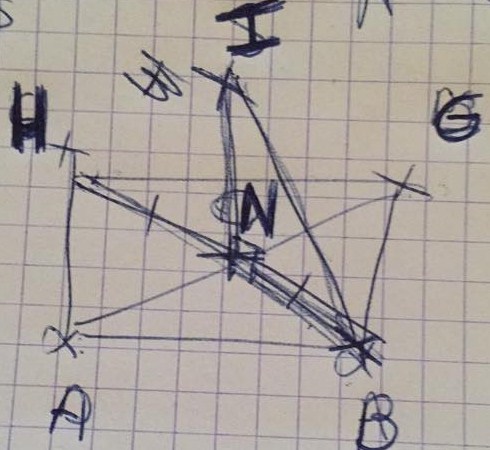
j'ai d'abord calculer le cote AH = 7.07cm car je sais que c'est un triangle rectangle ,
puis j'ai calculée HB =8.65 puis je les divisé en deux car je sais que le point N est son milieu donc BN = 4.32
en suite j'ai calculer IB car je sais que IFB est un triangle rectangle et enfin j'ai put calculer la hauteur car je sais que BNI est un triangle rectangle la hauteur vaut alors 7.06
voici les photos merci
Cela ne me paraît pas bon.
As-tu tenu compte de la longueur des côtés du cube (5 cm) ?
As-tu fait le dessin que je t'ai suggéré ?
D'une manière générale, je te conseille de conserver les valeurs exactes plutôt que de les remplacer par des valeurs approchées. Par exemple, il vaut mieux conserver  2 que de le remplacer par 1,41.
2 que de le remplacer par 1,41.
début du calcul correct, rien à redire.
la fin tu ne donnes pas les résultats intermédiaires mais ta hauteur est fausse
ensuite j'ai calculer IB car je sais que IFB est un triangle rectangle et enfin j'ai pu calculer la hauteur car je sais que BNI est un triangle rectangle
la hauteur vaut alors 7.06
attention le triangle BNI est rectangle en N, ne pas faire Pythagore à l'envers ! si c'est ça ton erreur.
une autre méthode de calcul bien plus rapide consiste à placer le point J milieu de CD
et à justifier que N est le milieu de IJ
et comme IJ se calcule de tête "instantanément" (IJ = FC !) ...
par ailleurs quand on enchaine des calculs on ne part pas d'une valeur intermédiaire arrondie pour poursuivre les calcul
on part d'une valeur exacte
au pire on garde l'intégralité de toutes les décimales de la calculette en enchainant les calculs sans sortir de la calculette (sans retaper de valeurs) avec les mémoires de la calculette au besoin.
ici on obtient les valeurs exactes AH = 5
 2 et pas 7.07, HB = 5
2 et pas 7.07, HB = 5 3 et pas un truc qui est parti de 7.07 déja arrondi, et réarrondi à la fin en un 8.65 inexact, alors que ça devrait donner 8.66 etc...
3 et pas un truc qui est parti de 7.07 déja arrondi, et réarrondi à la fin en un 8.65 inexact, alors que ça devrait donner 8.66 etc...Cette méthode m'a l'air plus simple mais avec quelle méthode je peut prouver que INJ sont alignés merci
ton point N étant l'intersection des deux diagonales AG et BH du cube est en fait le centre du cube
qui est "trivialement" au milieu de IJ (se placer dans le plan de symétrie verticale du cube, plan médiateur de [AB])
ceci dit avec les calculs "pas à pas" que tu as fait c'est tout à fait faisable aussi, il suffit juste de ne pas faire d'erreur et de calculer "de préférence" en valeurs exactes.
une autre méthode est via le volume de la pyramide
ce volume se calcule de plusieurs façons et en écrivant que ces différentes façons donnent le même volume, on obtient la hauteur de la pyramide
J'ai trouvé lA méthode :
Les points INJ sont alignés car si nous garçon la deuxième diagonale de la face FGCB elle coupera le segment GB qui est lui aussi une diagonale du carré FGCB le point d'intersection sera nommé K , en suite nous traçons une demi droite de K vers le cube nous pouvons remarquer qu'elle passe par N , nous pouvons en déduire que N est le milieu du cube ABCDEFGH , en suite nous pouvons tracer INJ cette droite passe par tout les points car le segment EC est égal au segment IJ
Donc EKC = INJ
Voila comment je démontre que les points INJ sont alignés merci de votre aide 😜
oui si tu veux, enfin le coup de la "demi droite de K vers le cube" ne convaincra personne  surtout si ça se poursuit par : nous pouvons remarquer qu'elle etc"
surtout si ça se poursuit par : nous pouvons remarquer qu'elle etc"
rédiger correctement et rigoureusement les trucs évidents sur les symétries du cube n'est pas si simple que ça 
il ne faut tout de même pas chercher midi à 14 heures et à mon avis ma démonstration par les diagonales BH et AG (que de toute façon tu avais déja considérées dans le rectangle de base de ta pyramide) me semble la plus directe et courte :
le centre d'un cube est l'intersection des "grandes diagonales" (qui joignent un sommet au sommet opposé du cnbe)
et il est "au milieu" des segments "médiateurs" des arêtes opposées et au milieu des segments joignant les centres de faces opposées, il est sur tous les plans de symétrie du cube etc...
démontrer ça "formellement" par des applications lourdingues de droites des milieux, parallélogrammes, de coupes dans tous les sens ne me semble pas nécessaire.


