Bonjour à tous !
Je poste ici car j'ai rencontré un petit soucis sur un DM de maths.
Voilà le début de mon DM :



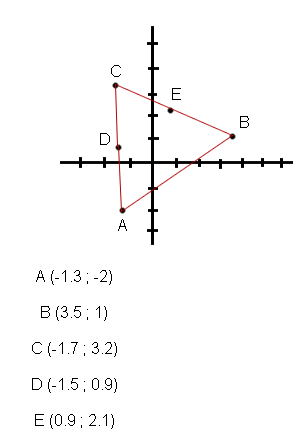
(Echelle non respectée ici, je l'ai vite refais sur photofiltre)
Je devais placer les points A, B, C, D et E, les relier, et faire une conjecture sur les droites (AB) et (DE) : on suppose qu'elles sont parallèles. Je devais également trouver les coordonnées du milieu du segment [AC] : c'est fait également, il s'agit des coordonnées du point D (j'ai justifié).

Mais je bloque ici : il faut prouver que les droites (AB) et (DE) sont parallèles. Pour cela, je dois utiliser la réciproque de Thalès, mais avant, je dois calculer la distance entre chaque point (je voudrais tous les calculer).

Je sais que la formule pour calculer la distance entre deux points A et B dans un repère orthonormé est :
(xb-xa)² + (yb-ya)²  [Le tout avec une racine carré mais je ne sais pas la faire sur le clavier]

Mais voilà là où je bloque : par exemple, sur la figure, je veux calculer la distance CE. Mais je ne sais pas si je dois calculer :

Racine carré de (xe-xc)²+(ye-yc)² OU racine carré (xc-xe)²+(yc-ye)²
En fait, je ne sais pas dans quel ordre mettre les points, et ce pour tous les points du graphique.

Ma question est donc : comment je détermine l'ordre dans lequel je dois les mettre ?
J'espère être assez claire dans mes propos ^^
Merci d'avance !