Inscription / Connexion Nouveau Sujet
calculer la limite d'une suite
Soit f(x) la fonction définie par :
f(x)= (6x²-2x+1)/(10x²-3x-1)
Déterminer la limite de f en - l'infinie
en -1/5 pour x<-1/5
en -1/5 pour x>-1/5
en 1/2 pour x<1/2
en 1/2 pour x>1/2
Pour les limites en -1/5 et 1/2 j'ai construit un tableau de signes
Par contre pour la limite en - l'infinie je ne sais pas trop comment faire.. Pourriez-vous m'aider ?
Soit f(x) la fonction définie par :
f(x)= (6x²-2x+1)/(10x²-3x-1)
Déterminer la limite de f en - l'infinie
en -1/5 pour x<-1/5
en -1/5 pour x>-1/5
en 1/2 pour x<1/2
en 1/2 pour x>1/2
Pour les limites en -1/5 et 1/2 j'ai construit un tableau de signes
Par contre pour la limite en - l'infinie je ne sais pas trop comment faire.. Pourriez-vous m'aider ?
On obtient donc lim (lorsque x tend vers - l'infinie) 6-2/x+1/x² = 6
et lim (lorque x tend vers - l'infinie) 10-3/x-1/x²) = 10 ?
ah oui d'accord merci
ensuite, pour la limite en -1/5 avec x<-1/5, j'ai trouvé + l'infinie
pour la limite en -1/5 avec x>-1/5 j'ai trouvé - l'infinie
et pour la limite en 1/2 j'ai trouvé + l'infinie pour x<1/2 et x>1/2
est-ce que cela est juste?
Merci
il faut remarquer que le dénominateur de f(x) qui est (10x²-3x-1) s'annule pour x=1/2 ou x=-1/5
..... à suivre...
OK pour les limites en -1/5
pour les limites en 1/2 ce n'est pas l'infini
6x^2-5x+1 s'annulent pour quelles valeurs de x ?
c'est faux
le dénominateur s'annule pour (1/2) et pour (-1/5)
factorise le numérateur , que remarques-tu ?
Concernant la limite de f(x) lorsqu'elle tend vers - l'infinie, la limite est-elle bien 6/10 ?
Merci d'avance
Je récapitule, j'ai trouvé que :
6x²-5x+1 s'annulait en 1/3 et 1/2
et que 10x²-3x-1 s'annulait en -1/5 et 1/2, ceci est-il juste ?
OUI les limites en l'infini sont justes ,tu peux simplifier 6/10 =3/5,
et celles pour -1/5 , sont justes aussi
et que 10x²-3x-1 s'annulait en -1/5 et 1/2, ceci est-il juste ?
le numérateur s'annule pour 1/2 OK
mais l'autre est fausse
oups j'ai confondu..
6x²-5x+1 s'annulait en 1/3 et 1/2 OK
et que 10x²-3x-1 s'annulait en -1/5 et 1/2, ceci est-il juste ? OK
d'où la fonction f non définie pour -1/5 et pour 1/2
cherche sa limite quand x tend vers 1/2
et je trouve donc + l'infinie lorsque x<-1/5 et - l'infinie lorsque x>-1/5
et + l'infinie lorsque x<1/2 et x>1/2
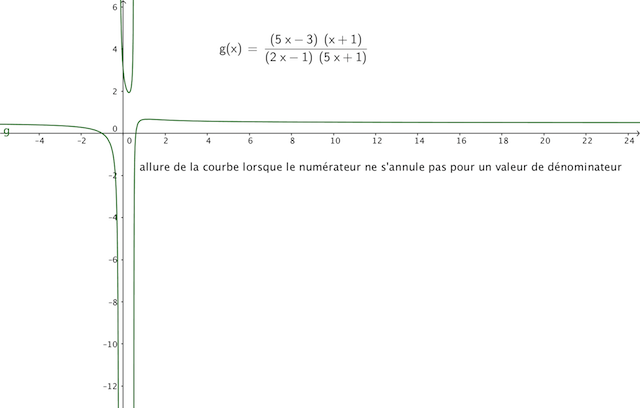
allure de la courbe lorsque le trinôme du numérateur ne s'annule pas pour une valeur qui annule le trinôme du dénominateur
Bonsoir Labo,
Je ne fais que de me promener.
Je crains fort que Marion éprouve quelques difficultés à interpréter les graphiques.
Bonsoir kenavo ,
je suis d'accord avec ta remarque, elle pourra essayer de les refaire à l'aide de geogebra ou autre logiciel
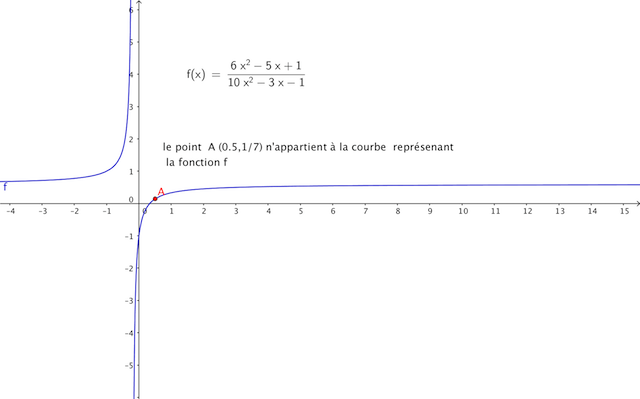
dans son cas ,si elle tape A=(0.5 f(0.5)) elle aura comme réponse indéfini
je poursuis...
si elle prend l'expression simplifiée h(x)= (5x+1)/(3x-1)
et si elle tape B=(0.5,h(0.5) ) le point B sera sur la courbe
c'est peut-être plus claire..
Mais comment se fait-il que d'après mon tableau de signe je trouve + l'infinie pour x<1/2 et x>1/2 alors?
encore merci pour toutes vos explications!
en général on fait un tableau de signe pour les variations d'une fonction , où tu indiques les limites au bornes des intervalles de définitions .
, mais pour déterminer les limites on fait des calculs en dehors du tableau
ici
tu calcules la valeur du numérateur pour x=1/2 et tu constates que le numérateur s'annule .. donc tu tombes sur une FI =0/0
mais puisque le numérateur s'annule , on peut mettre (2x-1) en facteur
il ne reste plus qu' à déterminer la seconde racine du numérateur ..pour obtenir l'expression simplifiée parde f
puis de calculer la valeur du quotient simplifé lorque x vaut 1/2
quand tu cherches la limite en 0.5 tu fais ce calcul
forme indéterminée..
si j'obtiens 0 au numérateur , cela veut dire que 1/2 est racine du trinôme , donc je peux factoriser (2x-1) , car 2x-1 s'annule pour x=0,5
donc je cherche la seconde racine ( que tu as trouvée)
donc on peut factoriser le trinôme
de même
1 s'annule pour x=1/2 et x=-1/5
d'où
ah oui!!!! d'accord je comprends mieux merci
du coup lim f(x) lorsque (x<1/2 et x>1/2)= 1/7 si j'ai bien compris ?