Bonjour,

Merci beaucoup pour la rapidité de la réponse.
Si j'ai bien compris je peux conjecturer le centre de symétrie de ma fonction si je connais les asymptotes à celles-ci ?
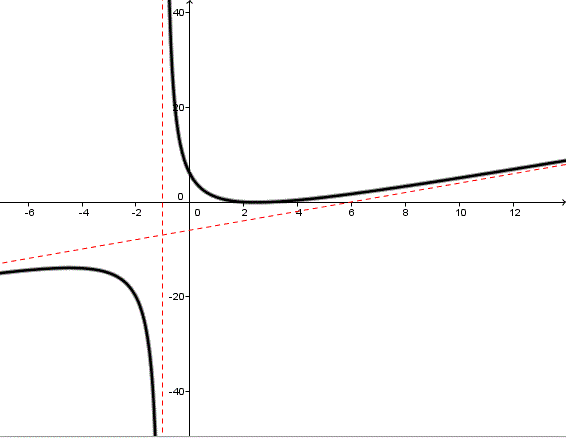
Dans le cas présent les asymptotes seraient respectivement les droites D1|y=x-6 et D2|x=-1. Du coup je peux conjecturer que le centre de symétrie de f correspond à l'intersection des deux asymptotes et serait alors le point C(-1,-7) puis je le prouve avec mon changement de repère.

Une manière parmi d'autres :

S'il y a 2 asymptotes et que la courbe admet un centre de symétrie, ce centre est alors à la rencontre des 2 asymptotes.

f(x) = (x²-5x+6)/(x+1)

asymptote verticale d'équation x = -1

f(x) = (x²-5x+6)/(x+1)
f(x) = (x-6) + 12/(x+1)

Donc la droite d'équation y = x-6 est asymptote oblique.

Si la courbe admet un centre de symétrie, les coordonnées de ce centre sont solutions du système :

x = -1
y = x-6

---> le candidat comme centre de symetrie est le point P(-1 ; -7)
-----
Si ce point est centre de symétrie, alors on aura : [f(-1 + X) + f(-1 - X)]/2 = -7  (1)

Vérifions si c'est le cas :

f(-1 + X) = ((-1+X)²-5(-1+X)+6)/(-1+X+1)
f(-1+X) = (1+X²-2X+5-5X+6)/X
f(-1+X) = (X²-7X+12)/X

f(-1 - X) = ((-1-X)²-5(-1-X)+6)/(-1-X+1)
f(-1 - X) = (X²+2X+1+5+5X+6)/(-X)
f(-1 - X) = (X²+7X+12)/(-X)
f(-1 - X) = -(X²+7X+12)/X

f(-1+X) + f(-1 - X) = (X²-7X+12)/X -(X²+7X+12)/X
f(-1+X) + f(-1 - X) = -14
[f(-1+X) + f(-1 - X)]/2 = -7  

(1) est bien vérifié.

Et donc le point P(-1 ; -7) est centre de symétrie de la courbe représentant f(x) = (x²-5x+6)/(x+1)
-----
Sauf distraction.  

Merci pour la réponse J-P.
Je vois maintenant comment faire un exercice de la sorte.
Merci beaucoup d'avoir pris le temps et la peine de me répondre.

salut

pour compléter ce que dit J-P ::

s'il y a deux asymptotes non parallèles !!!!

voir  :: Centre de symétrie la fonction


mais aussi regarder par exemple

Bonsoir Carpediem.
Après avoir regardé et réfléchi sur les exemples de fonctions que tu m'as proposé je trouve comme asymptotes pour la première fonction les droites d'équations x=4 et x=-2. Ces asymptotes sont parallèles et je ne trouve pas de potentiel centre de symétrie en regardant sur ma calculatrice.
Il en va de même pour la seconde où je trouve l'asymptote horizontale d'équation y=4 en plus des deux asymptotes verticales sus-citées.
Je ne remarque ensuite (graphiquement) aucune symétrie ou parité dans un repère centré en un point donné.

Ce qu'il me semblerait vraisemblable est que le centre de symétrie soit situé au milieu des deux asymptotes verticales, mais ma calculette n'a pas l'air d'accord avec ce raisonnement.

Normal, aucune de ces courbes n'admet de symétrie.

le critère sur les asymptotes est juste un guide pour conjecturer où se trouveraient un centre ou un axe de symétrie, s'il y en avait un

puisque si axe ou centre de symétrie il y a, c'est forcément un axe ou un centre de symétrie de la figure réduite à ces seules asymptotes.
le contraire étant évidemment faux : ce n'est pas parce que la figure formée par les asymptotes admet un centre ou un axe de symétrie que la courbe en a un !


ensuite de toute façon c'est les calculs ...

Merci pour la clarification Mathafou. C'est désormais plus net dans ma tête.

effectivement ces courbes n'ont pas de centre de symétries ...

par contre trace sur geogebra f(x) puis g(x) = f(1 - x) + f(1 + x) (tu peux même mettre n'importe quel nombre à la place de 1 (essaie avec 2 par exemple aussi))


ensuite crée le point A sur g et le point B = (-x(A),g(-x(A)))

crée ensuite le segment [AB] et anime A .... puis regarde ....

pardon c'est g(x) = f(a - x) - f(a + x)

mais tu peux aussi essayer avec + ....