Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup AlgèbreTopics traitant de algèbre [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

Centre du groupe des permutations

Posté par
robby3 31-05-24 à 18:34

Bonjour à tous,

Voici l'énoncé du problème:

Citation :
Déterminer le centre de S_n, pour 3\leq n


Voici mon raisonnement:

Le centre de S_n, noté Z(S_n) est l'ensemble des permutations p de S_n qui commutent avec n'importe quel élément \sigma de S_n.
Or si je prend un élément k de \{1,...,\} alors il existe bien une permutation \sigma de S_n qui va laisser fixe k et faire bouger les n-k autres éléments.
Donc je vais avoir \sigma(k)=k.

Ainsi si je prend un élément p de Z(S_n) alors j'aurais
\\ (\sigma o p)(k)=(p o \sigma)(k)=p(\sigma(k))=p(k)
Donc \sigma(p(k))=p(k) \Rightarrow p(k) est invariant par \sigma or le seul élément invariant par \sigma est k donc j'ai p(k) = k d'où p = I_n.

Ainsi Z(S_n)=\{I_n\}.

Est-ce que mon raisonnement est correct ?
Si oui, je ne comprends pas où intervient le 3\leq n

Merci d'avance de vos remarques et de votre aide.

Posté par
carpediemre : Centre du groupe des permutations 31-05-24 à 19:41

salut

ça me semble convenir ... mais tu pouvais utiliser ton sujet précédent en remarquant que \sigma \circ p = p \circ \sigma \iff \sigma \circ p \circ \sigma ^{-1} = Id

et que toute permutation se décompose en produit de cycles disjoints

pourquoi n = 3 : parce que S_1 = \{Id\} $ et $ S_2 = \Z/2 \Z qui sont évidemment "élémentaires" comme groupe

Posté par
robby3re : Centre du groupe des permutations 31-05-24 à 22:24

Carpediem>

Citation :
mais tu pouvais utiliser ton sujet

C'était un l'exercice juste après effectivement mais je n'arrivais pas à m'en sortir clairement...

Par exemple, si je dis que \sigma et \sigma^{-1} se décomposent en produits de cycles à supports disjoints, ça veut dire qu'ils commutent et donc je peux m'arranger pour que p = Id directement, c'est ça ?

Ok pour S_1
S_2=\mathbb{Z}/2\mathbb{Z} ou bien S_2 \cong \mathbb{Z}/2\mathbb{Z}

Merci de ta réponse !

Posté par
Sylvieg Moderateurre : Centre du groupe des permutations 01-06-24 à 06:57

Bonjour,
Une réponse un peu différente pour "je ne comprends pas où intervient le 3\leq n" :

Citation :
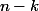il existe bien une permutation \sigma de S_n qui va laisser fixe k et faire bouger les n-k autres éléments.
Si n = 2, une telle permutation n'existe pas.

Posté par
Sylvieg Moderateurre : Centre du groupe des permutations 01-06-24 à 06:59

Et il y a une coquille :
"qui va laisser fixe k et faire bouger les n-1 autres éléments"

Posté par
robby3re : Centre du groupe des permutations 03-06-24 à 11:25

Bonjour Sylvieg,

Oui, merci pour la coquille !

Effectivement, c'est là qu'intervient le n plus grand que 3.
Merci !

Posté par
Sylvieg Moderateurre : Centre du groupe des permutations 03-06-24 à 15:29

De rien, et à une autre fois sur l'île \;


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1719 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !