Annuler
connectez vous
- Bissectrice et cercle inscrit dans un triangle - Cours 4ème
- Exercice Bissectrices et cercles inscrits dans un triangle
- Cours sur les Figures planes, Distance d'un point à une droite et Tangente à un cercle
- QCM : Figures planes, distance et tangente - Exercice 4ème
- Six Exercices de géométrie pure - quatrième
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques Collège cycles 3 /4On parle exclusivement de maths, niveau collège. QuatrièmeForum de quatrième GéométrieTopics traitant de géométrie [tout]Lister tous les topics de mathématiques
Niveau quatrième
cercle inscrit dans un triangle
Posté par Lulu58
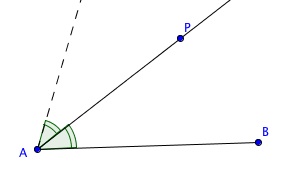
J'ai un segment AB et un point P situé au dessus .
Construis le point C tel que P soit le centre du cercle inscrit au triangle ABC . Justifie .
Bonjour , s'il vous plait , se serai pour m'aider à justifier cet exercice de maths .
Merci de m'aider .
OK
P est le centre du cercle inscrit dans le cercle
d'après la définition c'est que P sera à l'intersection de quelles droites ?
ok
donc si tu traces (AP) c'est la bissectrice de l'angle BAC
tu peux donc tracer cet angle qui sera le double de l'angle BAP
Est ce que cela suffit pour justifier que le cercle C est inscrit dans le triangle ABC ou dois je construire une autre bissectrice ? 
pour tracer le cercle on verra après...
d'abord on trace le point C pour avoir le triangle ABC
as-tu fait la 1ere construction au point A ?
et as-tu compris pourquoi on fait ça ?
(voir le schéma posté à 18h53)
Oui j'ai fait la 1er construction . Le point P appartient à la bissectrice donc il est equidistant peut etre au point C ?
Le tracé est faisable en 5ème car il n'utilise que les angles ("équidistant..." on verra après)
P est sur la bissectrice de BAC donc (AP) est la bissectrice de BAC
et donc on put tracer l'angle BAC comme le double de l'angle BAP
mais on ne sait pas encore où est C
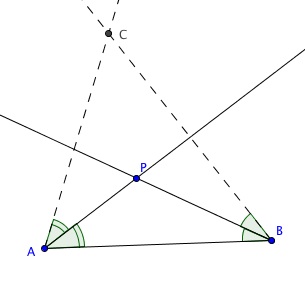
C est quelque part sur la demi-droite en pointillé sur mon shéma...
Pour trouver C , il faut faire le même raisonnement et le même tracé du côté de B
les deux demi-droites ainsi obtenues se coupent en C
l'angle ABP est égal à l'angle PBC car (BP) est la bissectrice de l'angle ABC
de plus "équidistant" tout seul ça ne veut rien dire ...
P est équidistant de 2 choses
lis-tu les infos que je te mets ???
as-tu fait le même tracé de côté de B que celui fait du côté de A ???
J'ai bien tracé la bissectrice partageant l'angle ABC en 2 comme c'est une bissectrice les 2 angles sont égaux ?? sinon je ne comprends pas pour faire la figure autrement ??
la bissectrice partageant l'angle ABC c'est (BP)
après avoir tracé (BP) as-tu tracé l'angle ABC : le double de ABP ?
oui le cercle a pour centre P
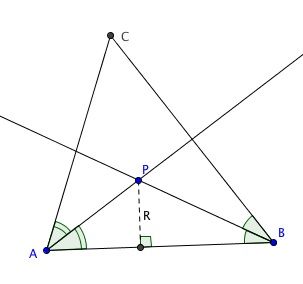
mais avant de le tracer il faut dessiner le rayon : la rayon est le segment perpendiculaire à [AB] partant de P
Oui , je l'ai bien marquer , je n'aurais plus cas justifier au propre .
Merci beaucoup de m'avoir aidée .
Bonne soirée .