Bonjour coa347.

supposons que nous ayons la négation de ce que tu demandes. Il suit qu'on pourrait avoir ceci :

soient a et b deux représentants de classes à gauche qui se trouvent dans une même classe à droite.



Il suivrait et donc et

Ainsi, cela contredit les qualités de a et b.

Une transversale ou une simple famille finie de représentants ?
Groupe fini ou pas ? Famille finie ou pas ?

Ulmiere Merci. Il s'agit d'une simple famille finie de représentants, groupe quelconque, indice de H dans G fini.

jsvdb Merci. Ta démonstration m'étonne car pour tout a, il est vrai que a est dans aH et dans Ha, et on conclurait au final que a est dans H.
Je crois que l'erreur se situe dans : b dans bHa ?

Oui, c'est pas clair mon truc, et là, je vois pas ...

Ok jsvdb.
Le problème est que je suis dans un exercice où il faut montrer qu'il existe une famille de représentants des classes à droite et à gauche, et que j'ai montré que toute famille de représentants.... J'ai donc dû faire une erreur, seulement je ne la vois pas.

Je cherche donc en même temps un contre-exemple.

Si quelqu'un a une idée...

En raisonnant sur les cardinaux, on peux trouver quelque chose. Je vais prendre un exemple pour illustrer.

Je considère un groupe fini non abélien G et H un sous groupe tel qu'il y a ait trois classes à gauche et à droite.
Je note H, G1,G2,D1 et D2 les classes.
Elles ont toutes |G|/3 éléments.
H,G1 et G2 forment une partition de G, ainsi que H, D1 et D2.

Soit a un élément qui ne soit pas dans H.
a est donc dans G1 ou G2 et dans D1 ou D2.
Pour fixer les idées, supposons a dans D1 et G1.

Soit b un élément de D2. Il n'est pas dans H est est donc nécessairement dans G1 ou G2.
S'il est dans G2, c'est fini, sinon, on choisit un autre élément de D2.
On conclut que si tous les éléments de D2 sont dans G1 alors G2 est vide, ce qui est absurde.
Il existe donc un élément commun à D2 et G2.

Merci jsvdb,

Si je comprends bien, ta démonstration porte sur le fait qu'il existe une famille de représentants communs aux classes à gauche et à droite. Cela doit être vrai car c'est le résultat de l'exercice.

Cela me fait pen[rouge][/rouge]ser que toute famille de représentants à gauche l'est aussi à droite, est faux. En effet, si c'est le cas, cela interdit que deux éléments qui appartiennent à deux classes différentes à gauche soient dans la même classe à droite (sinon ces deux représentants à gauche ne le seraient plus à droite), donc cela interdit les remaniements entre les classes. Donc cela veut dire que les classes à gauche et à droite sont les mêmes, i.e. H est normal. Ce qui n'est pas le cas général.

Cela répond donc à ma question (sauf erreur). Ce n'est pas toute famille ... . J'ai donc fait une erreur dans ma démo. Si j'ai le temps, je la posterai.

Et ta démo montre bien l'idée qu'il existe une famille commune de représentants à droite et à gauche. En effet si ce n'était pas le cas, une fois constituées les classes à gauche, il faudrait mettre tous les éléments du groupe dans la même classe à droite pour empêcher la répartition, donc la représentation, et ceci est impossible compte tenu du fait que les classes doivent contenir le même nombre d'éléments.

Nos messages se sont croisés.

Bonjour jsvdb,

Notre démo pour il existe ne tient la route que s'il y a 3 classes au plus (dont la classe neutre H) ! En effet, avec plus de 3 classes, on peut caser les éléments de la 3ème classe dans une 4ème et l'argument du nombre d'éléments dans une même classe tombe.

Je fais dans le cas fini.
Soit G groupe et H sous-groupe.
Soient H D1 ... Dn les classes à droite et H G1 ... Gn les classes à gauche.

Dans la suite, l'expression "faire correspondre" signifie "trouver un point commun entre"

On a vu qu'on pouvait faire correspondre  D1 et G1 (quitte à les renommer au besoin).
Supposons qu'on ait mis en correspondance D1 ... Dj respectivement avec G1 ... Gj.

Supposons D(j+1) ne puisse être mis en correspondance avec aucun des G(j+1) à Gn (autrement dit D(j+1) Gk = 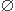pour k de j+1 à n).
Alors forcément, il existe un Dp avec j < p 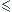n tel que Dp puisse être mis en correspondance avec G(j+1).
Sinon, on a un gros soucis de cardinalité : tout le groupe G, réparti en n classes à gauche, serait réparti en au maximum n-1 classes à droite, ce qui est absurde.

Dans le cas infini, on peut distinguer deux cas selon que H est d'indice fini ou pas.
Dans le premier cas, ça se fait comme dans le cas fini.
Dans le second, j'imagine qu'il va falloir passer par l'argument fini pour y arriver et qu'il va y avoir du choix dans l'air.

T'as tout lu ?

Oui

En effet, ça tient pas trop la route ma fin d'argumentation.
Bon bin là je sais pas comment poursuivre ... ni trop envie.

Bonsoir jsvdb,

Citation :
Je fais dans le cas fini.
....
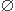Supposons D(j+1) ne puisse être mis en correspondance avec aucun des G(j+1) à Gn (autrement dit D(j+1) Gk = pour k de j+1 à n).
Alors forcément, il existe un Dp avec j < p 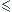n tel que Dp puisse être mis en correspondance avec G(j+1).
Sinon, on a un gros soucis de cardinalité : tout le groupe G, réparti en n classes à gauche, serait réparti en au maximum n-1 classes à droite, ce qui est absurde.

Messages croisés. Je n'ai pas trop envie de poursuivre non plus, mais cette propriété aussi évidente n'apparait pas facile à démontrer.

Ok, mais avant de quitter je livre un truc que j'avais écrit puis effacé :

on a une bijection naturelle entre l'ensemble des classes à gauche et à droite :



Plus précisément, si représente , alors

La bijection réciproque :



Peut-être à utiliser ...

Autre élément de réflexion :

ce problème est peut-être un problème ensembliste : soit G un ensemble et P, Q deux partitions de G à j éléments telles que chaque éléments de chaque partition contienne le même nombre n d'éléments de G. On a donc #G = jn.

Est-ce que tous les éléments de P et Q peuvent être représentée par une famille commune aux deux partitions ?

C'est exactement ça.

Bonjour,

Foxdevil je reproduis ici l'exercice qui m'a fait poser cette question.

Soit G un groupe et H un sous-groupe d'indice fini dans G.
Pour tout , ,  est appelée classe double de G modulo H.

a) montrer que le nombre de classes doubles est fini.

b) étant donné , vérifier que l'on a : , où , et
pour tout , et , si .

c) Prouver que l'on a : , où pour tout , et , si .

d) On pose , vérifier que .

e) En conclusion de ce qui précède, prouver que si , il existe dans G des éléments formant une famille de représentants, à la fois, de l'ensemble des classes à droite et de l'ensemble des classes à gauche modulo H.

J'ai fait jusqu'à d). Je sèche sur la e) (si quelqu'un a une idée..), ou plutôt, j'ai montré que toute famille de représentants des classes à droite, l'est aussi à gauche (ce qui est faux compte tenu de ce qui a été dit dans ce fil).

Finalement, si la e) est vraie comme conséquence de la théorie des ensembles (pour toute partition double d'un ensemble ...), cet exercice apparait un peu lourd pour démontrer juste ça.

... ... il y a une relation d'équivalence définie par : g R g' s'il existe h et k dans H tels que g'=hgk.

Ahhhh ... bah y'avait des questions avant pour aider ... t'aurais pu le signaler d'entrée de jeu 😢... ça m'aurait évité une nuit « presque » blanche.

Bonsoir jsvdb,

Ah désolée de t'avoir fait passer une nuit blanche. J'espère que tu as décroché la lune et trouvé une solution à notre problème !

Grâce à ce fil, j'ai quand même eu une réponse partielle au mien : pour toute famille ... (non) et il existe une famille ... (oui), mais je ne vois toujours pas où est mon erreur dans la e). J'ai beau relire 10 fois.

Pour mémoire, on essayait de démontrer "il existe une famille ..." avec la théorie des ensembles. Le faire avec les groupes me parait assez compliqué avec cet exercice.

Bah en fait c'est tout bête : il suffit de considérer tout simplement les donnés par d).

Les ensembles de l'union de d) sont tous disjoints (prouve le) et ils partitionnent la double classe, qui elles-mêmes partitionnent G.

Donc on prouve avec l'exo assez facilement qu'il existe une telle famille.

Quand à "toute famille", effectivement je suis sceptique.  Pourrais-je voir ta démo s'il te plaît ?

Bonjour Foxdevil et merci,

Les ensembles de l'union de d) sont tous disjoints : pas de problème, cela a été prouvé en b), vu que (car ), ils partitionnent la double classe : pas de problème, vu que leur union fait la double classe (par d) et que leurs intersections sont disjointes 2 à 2, et qui elles-mêmes partitionnent G : par définition de la relation d'équivalence sur G dont les classes sont les doubles classes.

En effet, vu comme cela, c'est tout bête. (je crois que j'avais perdu de vue que les HgH partitionnent G)

Je cherchais comment exhiber (par le calcul, en utilisant b) une telle famille de représentants  des classes à droite et des classes à gauche de G modulo H : mais si les sont une famille de représentants des doubles classes, alors les répondent au problème (l'union des classes fait G et leurs intersections sont disjointes 2 à 2 : facile à montrer).

Je posterai ma solution fausse de e) dans la journée.

Voici ma démonstration du e) :

Soit une famille de représentants des classes à droite de G modulo H. Donc .

Comme pour tout k, , on a , donc ,

soit (en utilisant d)

Avec a) : pour tout , donc , de même ,

en combinant avec ce qui précède, on obtient ,

donc toute famille de représentants des classes à droite de G selon H, l'est aussi à gauche.

Si tu as le courage, Foxdevil, de me dire où est l'erreur dans cette démonstration, merci d'avance.

... toute famille de représentants ...

Bonjour coa347,

Tous les passages de ton raisonnement me paraissent bons, excepté celui là:

Citation :
Avec a) : pour tout ,

Merci Foxdevil,

Heu ce n'est pas avec a), mais avec b), désolée.
Et mon erreur est là : compte tenu de , j'ai supposé que les , donc les   formaient une partition de .
C'est simplement (c'est l'hypothèse) les qui forment une partition de .
(j'aboutissais à , j'aurais pu m'en rendre compte )

C'est bien ce qu'il m'avait semblé


Dit en passant, plutôt que de laisser mourir le topic, la généralisation ensembliste proposée par jsvdb me semble fort intéressante. À creuser...

Je me demandais aussi si on pouvait utiliser ce résultat pour démontrer la proposition de jsvdb sur les ensembles, plus générale. A suivre ...

Bonjour coa347,

Je pense que oui. C'est aussi l'idée que j'avais. En fait, si on arrive à trouver une bijection entre deux ensembles qui respecte les partitions (deux partitions respectivement par ensemble), c'est gagné. Il faudrait à la rigueur trouver une condition (suffisante) pour qu'une telle bijection existe.
Si elle existe, alors la bijection répond au problème  (il suffira d'interpréter notre ensemble comme un groupe "au travers" de cette bijection).

De plus, le résultat serait alors généralisable au cas où les sous ensembles sont infinis (mais de même cardinalité).

Sinon, quelques petits schémas faits rapidement m'ont presque convaincu que le problème est purement combinatoire et devrait pouvoir se démontrer juste avec des outils combinatoires. Non seulement ces bijections existent, mais on devrait pouvoir les dénombrer exactement. Ou dénombrer le nombre de famille de représentants des deux partitions. Il y a probablement un lien entre les deux.

Mais j'avoue ne pas y avoir réfléchi plus que ça (et avoir un peu la flemme aussi)

Bonjour Foxdevil,

Si E est un ensemble de cardinal mxn, on peut le partitionner en n classes de m éléments. On suppose qu'on a deux telles partitions de E, pour lesquelles on cherche un système de représentants commun.
Pour pouvoir utiliser le résultat sur les groupes, il faut trouver un groupe G non commutatif d'ordre mxn (je ne sais pas si c'est toujours possible, il me semble que oui), un sous-groupe non distingué H de G, puis il faut mettre en bijection E et G de telle sorte que les deux partitions de E coïncident avec les deux partitions (G/H)d et (G/H)g. Puis on peut transposer la loi de G sur E pour faire de E un groupe (mais c'est inutile).

Il reste encore un problème dû au fait que les deux ensembles quotients à droite et à gauche de G selon H ont une classe commune H, ce qui n'est pas forcément le cas de E. Donc il faut agrandir G en mx(n+1) éléments, pour pouvoir éliminer ensuite la classe commune H et faire la bijection sur G privé de H.

Tout cela ne me parait pas évident à mettre en oeuvre, surtout trouver H de telle sorte que les classes à droite et à gauche de G coïncident avec les classes des partitions de E. Il faut que les répartitions coïncident...

Bonsoir coa347,

Bon, j'avoue qu'après avoir cherché un peu je sèche. J'ai jamais été fan de la combinatoire . Du coup, je mets mes idées ici si jamais ça inspire quelqu'un.

On a pas besoin de faire tout ce que tu dis car apparemment le problème se résoudrait de manière purement combinatoire (je parle d'une preuve sans utiliser le résultat sur le Groupe, qu'on vient de montrer).

Soit un ensemble et deux partitions et de , où # #. On suppose que tous les sous-ensembles de peuvent être mis en bijection entre eux et avec n'importe lesquels des sous-ensemble de .

On appelle famille de représentants d'une partition , une famille , où .

On commence par montrer qu'il existe une famille de représentants commune à et si et seulement si il existe une bijection à la fois de et de dans , avec au moins un point fixe entre chaque et tels que .

La famille de points fixes nous fournit alors la famille de représentants commune à et .

Si une telle bijection existe, alors il semblerait bien qu'on puisse même les dénombrer (dans le cas fini). Le plus étonnant semble être que dans le cas où est fini, une telle bijection existerait toujours! (bon j'ai pas fait des tests hyper poussés non plus....)

Le tout est de construire cette bijection (ou de prouver que son inexistence est absurde). J'ai un algorithme de construction qui semble bien répondre à la question. Mais je suis incapable de prouver qu'il finit par donner une telle bijection.

Bonjour Foxdevil,

Je suis d'accord avec toi pour dire qu'on n'a pas besoin des groupes pour démontrer ce que l'on cherche à montrer : de toute façon, cela parait infaisable.

Il y a des passages dans ce que tu écris que je ne comprends pas, par exemple, je ne vois pas comment il peut exister une bijection de G dans P' étant donné que ces deux ensembles n'ont pas le même nombre d'éléments (les éléments de P' sont les classes d'éléments de G).
Je verrais une bijection entre les classes de P, entre les classes de P', et entre une classe de P et une classe de P' (on aura ainsi toutes les bijections voulues).
Mais la bijection de classe à classe dans une même partition me gêne, car elle ne rend pas compte que les classes sont disjointes. Une bijection entre les classes de P et celles de P' induit un ensemble de permutations de G.
La clé semble être le même nombre de classes (c'est évidemment faux si le nombre de classes est distinct entre les deux partitions), donc un raisonnement élément par élément va échouer.
Je ne comprends pas non plus "construire une telle bijection" : on en a une arbitraire, il faut montrer qu'elle marche.

Je sèche aussi, mais je n'ai pas beaucoup de temps pour y réfléchir (je prépare le M1 à distance).

Je pense avoir trouvé en y réfléchissant un peu plus :

On part d'une situation initiale où on a réparti les éléments dans des classes de même nombre d'éléments (ou dans des partitions en bijection pour un nombre infini d'éléments) .
On échange deux éléments :
- s'ils sont dans la même classe, on a toujours un système commun de représentants entre les deux situations avant et après;
- s'ils sont dans deux classes différentes, idem ....... (évident).
Etant donné que deux situations diffèrent par un échange deux à deux d'éléments au bout d'un nombre fini d'étapes (décomposition d'une permutation en produit de transpositions), on passe ainsi d'une situation à l'autre.

Alors je m'explique mieux parce tout n'était peut être pas clair.

OUI!!!!

Grâce au Théorème de Hall!!!

Il suffit de montrer que toute sous partie de a au moins arrête en commun avec , ce qui est évident.
En effet, étant donné que est une partition de , pour chaque , il existe tel que l'arrête soit dans le graphe. Donc on a bien au moins arrête en commum avec . D'après le théorème, il existe un couplage parfait.
Ce couplage parfait nous donne la bijection de vérifiant les 2 propriétés:
- Bijection de sur (par définition d'un couplage parfait).
- On envoie n'importe quel sur lui même, puis on répartit le reste des sur les éléments restants de (de même cardinal, donc facile).

On a construit notre bijection!!!

Ainsi, il existe toujours une telle bijection, et cette bijection nous fournit un système de représentant commun aux deux partitions (dans le cas fini).

Corollaire: Dans tout groupe G avec H d'indice fini dans G, il existe toujours un système de représentants de classe à droite et de classe à gauche modulo H.

Preuve: Deuxième preuve. Appliquer le résultat d'avant aux classes à gauche et à droite (qui sont toutes deux des partitions de G).

Bonjour Foxdevil,

Oui, une bijection de G virgule, et de P' dans P ... Et ma démo ne marche effectivement pas, les permutations entre éléments ne sont pas la solution, ils ne rendent pas compte des partitions.
Je ne peux pas vérifier ta solution, tous les théorèmes que tu cites me sont inconnus. Mais c'est quand même étonnant qu'un problème en apparence simple, n'ait pas de solution simple (je sais bien ...).

Bonjour coa347,

Avec les différents liens que j'ai mis tu peux comprendre assez facilement. N'hésite pas si tu as des questions. En plus, la preuve du théorème de Hall n'est pas très difficile.

(le gars qui lâche pas l'affaire )