Inscription / Connexion Nouveau Sujet
Conjecturer la position relative de fonctions
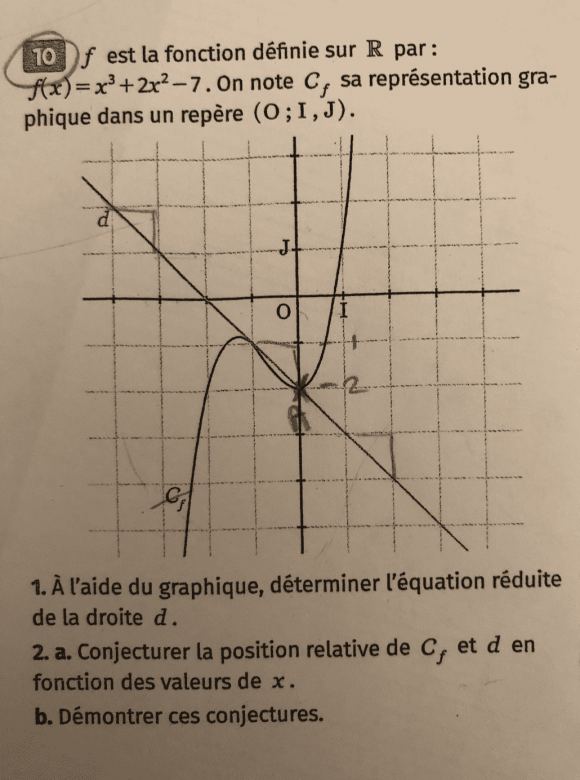
Bonjour sur cet exercice, il nous est dit : f est la fonction définie sur R par : f(x) = x^3+2x^2-7. On note Cf, sa représentation graphique dans un repère. (O, I, J).
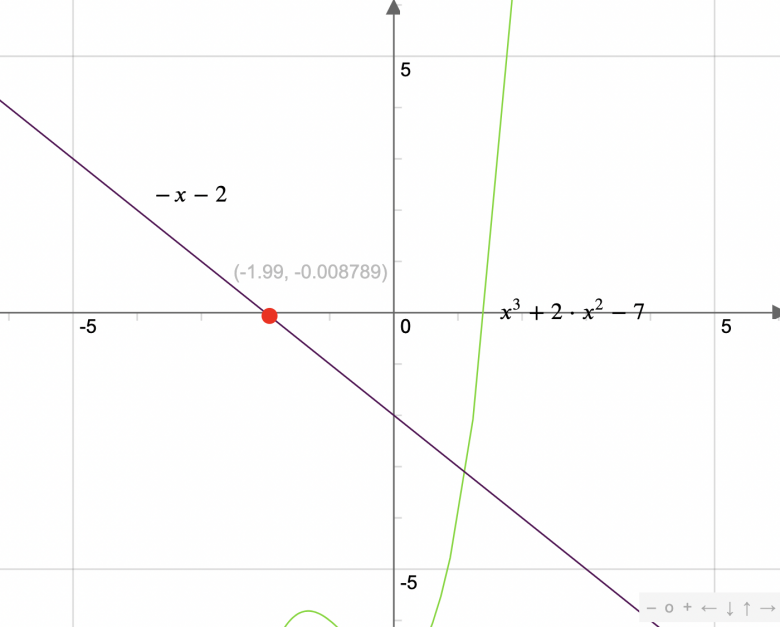
1. A l'aide du graphique, déterminer l'équation réduite de la droite d. J'ai trouvé grâce au graphique que l'équation de la droite était -x-2.
2.a. Conjecturer la position relative de Cf et d en fonction des valeurs de x. J'ai essayé de faire f(x)-d = 0 pour déterminer le point d'intersection mais il est impossible de factoriser x^3+2x^2-7-(-x-2). Je me suis donc demandé si on pouvait trouver le point d'intersection en disant qu'on l'avait trouvé à l'aide de la calculatrice et ensuite on disait que comme f(x) était au dessus ou en dessous de d f(x)-d était négatif ou positif.
Cependant la question b de la 2e question me demande de démontrer les conjectures. Je ne sais donc pas comment faire car j'ai trouvé le point d'intersection à l'aide de la calculatrice. Faut-il que je prouve ces conjectures en soustrayant des point de f(x) et de d ?
Vous trouverez l'exercice complet et une représentation graphique des courbes faite en ligne en PJ.
bonjour,
conjecturer : c'est dire ce que tu peux en penser en regardant la figure.
Pour conjecturer, il n'y a pas de calcul à faire.
Que peux tu répondre en 2a) ?
Je peux répondre que la courbe Cf est en dessous de d de -l'infini à un point non connu et au dessus de d de ce point inconnu à + l'infini
Bonsoir
Juste de passage je ne comprends pas le graphique. Si l'on dit que le repère est (O ; I, J) cela veut dire OI=1 et OJ =1
La courbe devrait donc couper l'axe des ordonnées au point d'ordonnée et non aux environs de
hekla, l'erreur est corrigée.
Hexperthyse
f(x) = x^3 +2x² -2
(d) : y=-x-2
ta conjecture : en effet, de -oo à x= 0, la courbe est en dessous de la droite, elle est au dessus ensuite.
pour démontrer : ta démarche est bonne.
f(x) - y = x^3 + 2x² + x
tu peux factoriser !
f(x)-d = x^3+2x^2-2-(-x-2) = x^3+2x^2-2+x+2 = x^3+2x^2+x = 0
On factorise :
x(x^2+x+1) = 0
Si A*B = 0 alors A = 0 ou B = 0
Soit x = 0 soit x^2+x+1 = 0 (identité remarquable : a^2+2ab+b^2
(x+1)^2 = 0 et comme A^2 = 0 alors A = 0
Donc x+1 = 0 avec x = -1
oui, c'est très bien.
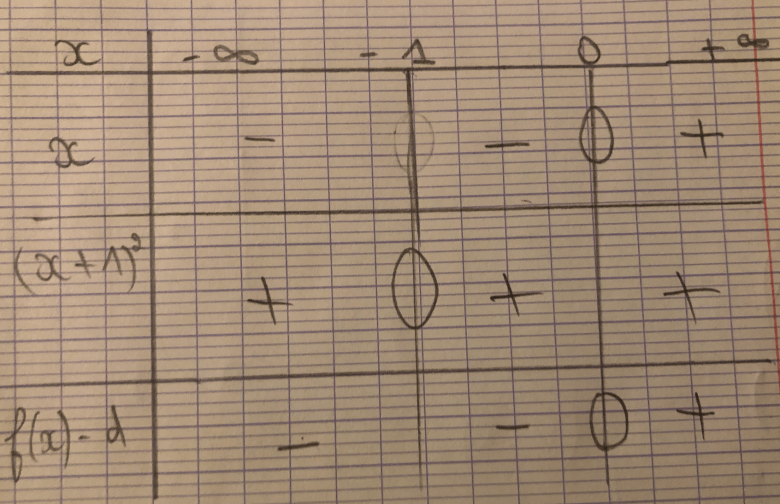
f(x)-d = 0 pour x=-1 ou x=0
mais ce qui nous intéresse c'est le signe de f(x)-d
donc le signe de x (x+1)²
soit tu sais conclure tout de suite, soit tu fais un tableau de signes.
tu peux remarquer que (x+1)² est toujours positif ou nul.
donc dans x (x+1)² seul le signe de x compte.
f(x)- d < 0 quand x<0 ==> ça correspond à quelle situation avec les courbes ?
ta conjecture, c'était bien la position des courbes, n'est ce pas ?
là, en question 3, tu as regardé le signe d'une expression.
tu dis
f(x)-y < 0 quand x <0 (c'est juste)
est ce que ta conjecture (avec les courbes) est vérifiée ?
Oui c'est vérifié car ma courbe Cf est en dessous de d pour tout x<0. Pour mon tableau de signe je n'inscris pas -1 dessus du coup car le signe de f(x) - d ne change pas. Les courbes se touchent seulement n'est ce pas?
oui, c'est ca !
quand x < 0, f(x) - y < 0 donc f(x) < y et Cf est en dessous de (d).
quand x > 0, f(x) - y > 0 donc f(x) > y et Cf est au dessus de (d).
tout est clair pour toi ?
Super merci beaucoup pour votre aide du coup pour la démonstration des conjectures j'utilise quelle méthode le tableau de signes ou
quand x < 0, f(x) - y < 0 donc f(x) < y et Cf est en dessous de (d).
quand x > 0, f(x) - y > 0 donc f(x) > y et Cf est au dessus de (d).
QU'est il mieux d'utiliser?
tu fais une confusion :
pour trouver le signe de f(x) -y :
- soit tu remarques que seul le signe de x compte, puisque (x+1)² est toujours positif ou nul, donc f(x)-y a le même signe que x
- soit tu fais un tableau de signes (comme tu l'as fait).
(NB : ecris f(x)-y au lieu de f(x)-d . (d ) est une droite, pas une équation.
Ensuite, et ensuite seulement, il faut terminer par :
quand x < 0, f(x) - y < 0 donc f(x) < y et Cf est en dessous de (d).
quand x > 0, f(x) - y > 0 donc f(x) > y et Cf est au dessus de (d).
Quand tu fais un tableau de signes, tu analyses le tableau pour répondre à la question, n'est ce pas? Ici, c'est pareil, ces phrases sont la réponse à la question suite à l'analyse du signe de f(x)-y, que tu fasses un tableau ou pas.
Si tu préfères présenter un tableau, fais le, mais il faut quand même que tu analyses le tableau et que tu apportes une conclusion qui vérifie ta conjecture.
OK ?
Ah d'accord j'ai tout compris merci beaucoup mais
quand x < 0 et Cf est en dessous de (d)
quand x > 0 et Cf est au dessus de (d) ça je le dis déjà dans la questions 2)a). Ai-je besoin de le rajouter?
dans la 2a) tu as conjecturé en regardant le dessin.
Apparemment, Cf est en dessous de (d) quand x <0.... etc..
dans la 2b), tu démontres, tu prouves que ta conjecture était bonne.
à l'issue de tes calculs (facorisation, tableau de signes, etc...), tu fais une conclusion , tu démontres que Cf est en dessous de (d) quand x<0, etc...
donc la conjecture était correcte, elle est démontrée.
tu vois ?
C'est super que tu aies compris.
Depuis que je suis en retraite, j'accompagne des élèves en difficulté avec les maths. Pourquoi poses tu la question ?
Je me suis posé la question car je trouvais que vous expliquiez vachement bien et je m'étais douté que vous étiez professeur. En tout cas merci beaucoup pour vos explications