Inscription / Connexion Nouveau Sujet
Connexes et convexes
Salut! J'ai vraiment besoin d'aide pour cette exercice, merci d'avance. Voila le sujet:
f(x)=
i=1i=n-1(xi2xn2 et A={x
n :f(x) différent de 0}
1. Montre C1={xn :f(x)<0, xn>0} et C2={xn :f(x)<0, xn<0} sont convexes et que
C3={xn :f(x)>0} est connexe par arcs. J'arrive à le voir sur une figure en dimension 2 mais je n'arrive pas à le montrer.
2. Montrer que les Ci sont les composantes connexes de A
Merci
Excusez moi f=(xi2-xn2) pour i variant entre 1 et n-1
Bonsoir;
1.On pourra commencer par remarquer que et
sont symétriques par rapport à l'origine de
et par suite la convexité de l'un entraine celle de l'autre.
Pour établir la convexité de par exemple remarquons que:
où
Soit alors et
on a
Merci elhor_abdelali de m'aider. Mais dsl, j'ai encore beaucoup de questions.
Est ce qu'on peut aussi pour montrer que C1 est connexe, montrer que f(tx+(1-t)y)<0?
Comment peut on montrer que C3 est connexe par arcs?
Est ce q'on pourrait m'explique ce qu'est exactement une composante connexe et comment peut on montrer que les Ci sont des composantes connexes?
Merci d'avance
Bonjour frosties ;
Est ce qu'on peut aussi pour montrer que C1 est connexe, montrer que f(tx+(1-t)y)<0?
Je suppose que tu as voulu écrire convexe à la place de connexe si c'est cela il faut montrer que :
Comment peut on montrer que C3 est connexe par arcs?
Je crois qu'il faut en outre supposer
(sauf erreur)Merci
oui car j'ai fait un schéma en dimension 2 et c3 n'est pas connexe
Le prof nous a corrigé cette question et je n'ai pas compris sa correction qui est la suivante
[x,x']
c3
[y,y']c3
[x',y]c3 si 0 n'appartient pas à [x',y']
x et y peuvent etre reliéz par [x,x']
[x',y][y,y']
x
(x1,...,xn-1,0)=x'
y(y1,...,yn-1,0)=y'
Je ne comprends pas en quoi ca montre que C3 est connexe par arcs
Et c'est quoi une composante connexe
Merci
Bonsoir frosties ;
Pour comprendre la connexité par arcs de on va se placer dans
(il se passe exactement la même chose en dimension supérieure).
Il est alors facile de voir que pour on a
et par suite
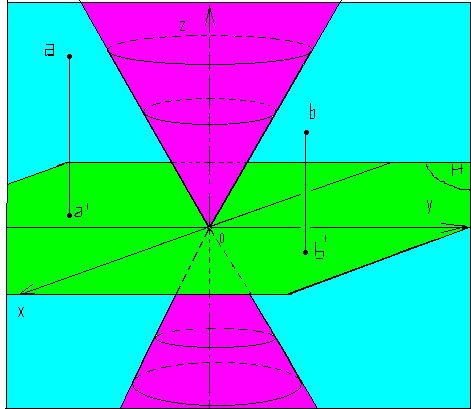
est l'extérieur du cône de révolution d'équation
(cône en move dans le dessin) la connéxité par arcs de
exprime le fait qu'étant donné deux points quelconques
et
de l'extérieur du cône on peut trouver un chemin allant de
vers
( ou de
vers
) tout en restant à l'extérieur du cône.
La solution de votre professeur est :
(*)aller de à son projeté orthogonal
sur l'hyperplan
de côte nulle.
(*)aller de à son projeté orthogonal
sur l'hyperplan
.
il est facile de vérifier que ces deux chemins sont extérieurs au cône.
(*)On aurait aimé aller directement de vers
et ce sera gagné parcequ'alors le chemin
va de
vers
( ou de
vers
) tout en évitant le cône mais
peut appartenir au segment
Seulement donc on peut aller de
vers
en évitant
Merci beaucoup, vous m'avez vraiment aider à comprendre cet exercice 
A ton service frosties ;
Pour ta question sur ce qu'est une composante connexe d'une partie de
:
Ce sont des parties de qui sont connexes et maximales au sens de l'inclusion , je m'explique :
prenons l'exemple de qui n'est pas connexe puisqu'on ne peut pas par exemple emprunter un chemin continu pour aller de
à
tout en restant dans
( le zéro est inévitable )
On peut trouver un tel chemin pour aller par exemple de à
:
qui est une partie connexe de
mais qui n'est pas une composante connexe de
parce qu'on peut trouver plus grand ( au sens de l'inclusion )
par exemple.
Par contre est une composante connexe de
(vu qu'on ne peut pas trouver plus grand sans perdre la connéxité).
a exactement deux composantes connexes
et
Annuler
connectez vous
topologie en post-bac