Inscription / Connexion Nouveau Sujet
Construire une section par un plan
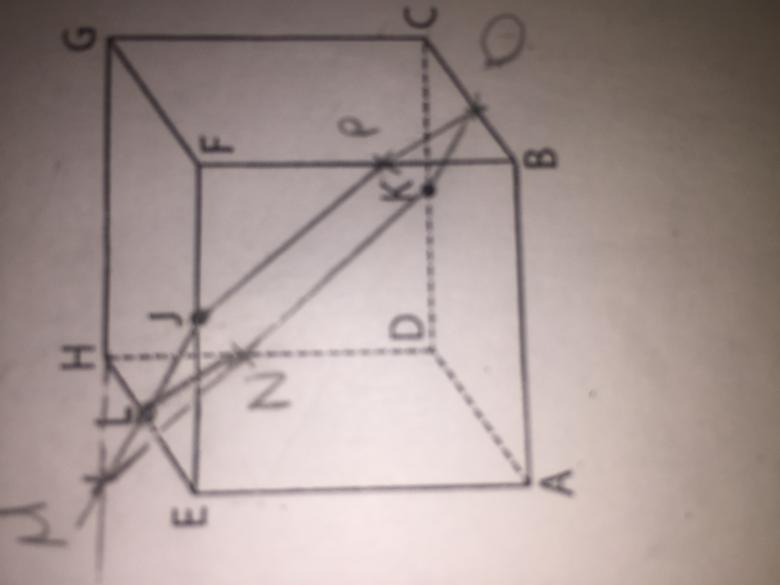
Bonjour est ce que vous pouvez m'aider à faire la section des cubes par le plan (IJK)
1er fugure =
EL=1/4EH
EJ=1/4EF
AK=3/4AB
2ème figure =
J,k.L milieux respectifs des segments [EF], [DC] et [EH]. Quel polygone obtient ton ?

salut
figure 1 : que peux-tu dire des droites (AE) et (JK) ?
figure 2 : que peux-tu dire des droites (JL) et (GH) ?
bon on va reprendre calmement et uniquement avec la figure 1 ...
mais à une condition tu apprends à écrire correctement les choses ... que ce soit en français ou en mathématiques !!
n'oublie pas que tu vas passer le bac dans moins de pas longtemps !!
que peux-tu dire des droites (AE) et (JK) ?
CE point est sur la face gauche
Donc on peut le relier au avec le point L
et pourquoi veux-tu faire cela ?
Merci de m'avoir rappelé que je n'étais plus au collège j'avais complètement oublier !
Je veux faire ça car je suis bloqué
Bonjour,
"réactions de collège" :
"la face gauche" alors qu'on a des noms de points pour parler de cette face de façon précise
"je veux faire ça parce que je suis bloqué"
(ça veut dire "je ne sais pas pourquoi, mais on verra bien ...")
réaction Terminale :
je sais ce que je cherche :
à tracer l'intersection d'un plan dont je connais le nom, dont je connais des points et des droites qui appartiennent à ce plan et que je peux les nommer,
avec un autre plan dont je connais le nom , des points et des droites de ce plan que je peux nommer
je sais que cette intersection est une droite (si les plans se coupent)
pour la tracer il suffit d'en connaitre deux points
quels sont les points que je connais qui appartiennent à la fois aux deux plans ? pourquoi appartiennent ils à ces plans ?
on n'est certes pas obligé de tout détailler à la virgule près de ce raisonnement
mais il doit de toute façon être présent en tête
et quand on demande "pourquoi" on doit pouvoir répondre précisément.
tu n'as absolument pas tracé le point M, nommé M et écrit M dessus, dont on a parlé,
et ce point est fondamental dans la construction telle qu'on l'a commencée (et autant poursuivre avec cette méthode là, elle marche très bien)
c'est lui qui va donner la suite
tu parlais de tracer ML ("ce" point on l'a appelé M, pour en parler on dit M et pas "ce point")
et je te repose la question pourquoi ?
est ce que M et L appartiennent tous deux à deux plans dont on cherche l'intersection
? si oui lesquels ?
rappel : on cherche les intersections du plan (JKL) avec chacune des faces du cube, et le jour où tu nommeras "la face de gauche" par son vrai nom tu trouveras ...
de toute façon ce n'est certainement pas en traçant des segments aux hasard complet comme tu le fais que tu trouveras ...
c'est en raisonnant
chaque trait ou point tracé doit être justifié
parce que telles droites appartiennent au même plan unique (et ne sont pas parallèles) donc elles se coupent
et si elles n'appartiennent pas au même plan réellement, eh bien elles ne se couperont jamais.
même si sur la figure les tracer en donne l'illusion (l'une est en vérité derrière l'autre au prétendu point d'intersection, c'est une illusion d'optique de croire quelles se couperaient, due à la perspective, c'est comme si tu prétendais que les arêtes EF et HD du cube se coupent ! )
Rebonjour excusez moi du retard,
. tu n'as absolument pas tracé le point M, nommé M et écrit M dessus, dont on a parlé,
et ce point est fondamental dans la construction telle qu'on l'a commencée (et autant poursuivre avec cette méthode là, elle marche très bien)
c'est lui qui va donner la suite
tu parlais de tracer ML ("ce" point on l'a appelé M, pour en parler on dit M et pas "ce point")
C'est fait j'ai nomé le point M sur la figure
et je te repose la question pourquoi ?
est ce que M et L appartiennent tous deux à deux plans dont on cherche l'intersection
? si oui lesquels ?
rappel : on cherche les intersections du plan (JKL) avec chacune des faces du cube, et le jour où tu nommeras "la face de gauche" par son vrai nom tu trouveras ...
Le point M et L appartiennent tout deux à la face EADH. (et à la face EHGF ? Je suis pas sûr pour le point M )
.de toute façon ce n'est certainement pas en traçant des segments aux hasard complet comme tu le fais que tu trouveras ...
c'est en raisonnant
J'avais pas fait au hasard mais en appliquant une propriété des droite parallèle : j'essayer de construire une droite qui passe par le point M et qui soit parallèle a LJ.
notons M le point d'intersection des droites (KJ) et (AE) ...
que peux-tu dire de ce point ?
J'y est répondu les droites (KJ)et(AE) se coupent en un point qui est le point M. Ce point est situer sur la face EHDA et de même pour le point L.
la face EHGF n'a rien à faire là
M est par construction l'intersection (dans le plan (ABFE) de la droite (AE) et de la droite (JK) :
M appartient à la droite (AE) qui elle même appartient aux plans (ABFE) et (EADH)
M appartient à (JK) qui appartient aux plans (ABFE) et (JKL))
M qui appartient à la fois aux plans (EADH) et (JKL)) appartient donc à leur intersection
ça tombe bien, on cherche justement l'intersection du plan (JKL) avec le plan (EADH) !!
L aussi appartient à ces deux plans (je te passe les détails), donc à leur intersection
donc la droite (ML) est l'intersection du plan (JKL) et du plan (EADH)
il n'y a plus qu'à "restreindre" cette intersection au segment qui se trouve à l'intérieur du carré EADH
ce qui donne un nouveau point de la section cherchée
appelons le N
terminer la section est alors immédiat
mais en appliquant une propriété des droite parallèle
c'est ça que j'appelle "tracer des trucs au hasard"
on a entendu parler d'un théorème quelconque, on ne le connait pas vraiment mais on sait juste qu'il parle de parallèles, alors tiens pourquoi pas et si je traçais une parallèle ...
la parallèle à (LJ) en M est cette droite :

comme elle est parallèle à (IJ), elle est dans un plan parallèle à (EFGH) : le plan (MTW) à la distance EM de (EFGH) et est largement au dessus de tout le cube
et donc ne risque pas de couper aucune des arêtes de ce cube !!
le point V est ici l'intersection de cette droite avec le plan (BCGF)
bref cette parallèle là n'a rigoureusement aucun rapport avec ce qu'on cherche ...
et tes prétendus points d'intersections de cette droite avec quoi que ce soit ne sont que des illusions.
peut être t'a-t-on ailleurs ou un pote ou le prof parlé de tracer une parallèle à (JL)
elle n'a rien à voir avec la construction entamée ici, et elle ne passe pas par M du tout.
cest une autre façon complètement différente de construire la section cherchée.
la construction telle qu'on l'a commencée (et autant poursuivre avec cette méthode là, elle marche très bien)
et cette construction qu'on a commencée ne fait intervenir aucune parallèle.
J'y est répondu les droites (KJ)et(AE) se coupent en un point qui est le point M. Ce point est situer sur la face EHDA et de même pour le point L.
faux, tu n'avais pas dit ça à l'époque
tu l'as dit seulement maintenant (le 12-05-18 à 10:36)
Les droites (KJ) et (EA) sont sécantes et se coupent en un point.

CE point est sur la face gauche
ça sert à quoi de citer une vielle réponse qui était incomplète et imprécise ?
alors que la réponse complète et précise a été donnée depuis !
c'est certainement pas ça qui va faire avancer la chose, alors que ta droite (ML) n'est toujours pas tracée !
ah bein, voila ! et c'est fini.
comme tu as parlé de parallèles tout à l'heure, une autre construction possible, complètement différente :
théorème
les intersections d'un plan avec deux plans parallèles sont des droites parallèles
ici les intersections du plan (JKL) avec les deux plans parallèles (ABCD) et (EFGH) sont donc des droites parallèles
où
on connait l'intersection de (JKL) avec (EFGH) : c'est la droite (IJ)
on connait un point de l'intersection de (JKL) avec (ABCD), un point que l'on sait dès le départ appartenir à ces deux plans là
donc on peut tracer l'intersection de (JKL) avec (ABCD)
cette autre construction est peut être plus simple à décrire car elle ne fait pas intervenir de point auxiliaire M, mais par contre elle nécessite le tracé de parallèle et que ABCDEFGH soit effectivement un cube (au moins un prisme droit)
la construction initiée par carpediem se trace à la règle seule et marche même si les faces de ABCDEFGH ne sont ni carrées ni parallèles entre elles
oui et je voulais proposé cette deuxième méthode pour la figure 2 (même si on peut s'en passer et travailler de la même façon qu'avec la figure 1) ...
une remarque : les parallèles vont de pair avec le théorème de Thalès qui n'est pas la loin ...

Oui merci c'est cette méthode que j'essayais de faire.
Pour la figure 2 , les droites (JL) et (GH) sont sécantes et se coupent en M qui est par construction l'intersection.
M appartient au plan (AEHD) et (EHHF)

"qui est par construction l'intersection."
phrase inachevée qui n'a donc aucun sens.
M appartient au plan (AEHD) certainement pas !!
et (EHHF) ??? faute de frappe (EHGF) oui.
par contre il appartient à deux autres plans intéressants
car M sur (HG) qui appartient à plusieurs plans (EHGF) certes, mais aussi un autre
et M sur (LJ) qui appartient à un plan éminemment intéressant (autre que (EHGF) vu qu'on cherche précisément l'intersection de ce plan là avec le cube
« par contre il appartient à deux autres plans intéressants
car M sur (HG) qui appartient à plusieurs plans (EHGF) certes, mais aussi un autre »
M sur (HG) appartient au plans (HGDC) non ?
« et M sur (LJ) qui appartient à un plan éminemment intéressant (autre que (EHGF) vu qu'on cherche précisément l'intersection de ce plan là avec le cube »
M sur (LJ) appartient au plan (FEAB)
M sur (HG) appartient au plans (HGDC) non ? oui
M sur (LJ) appartient au plan (FEAB) certainement pas
tu as vraiment l'impression que la droite (LJ) est dans le plan (FEAB) ???
le plan dont je cherche à te faire dire le nom est cité directement et textuellement dans l'énoncé (pas sur la figure)
on cherche précisément l'intersection de ce plan là avec le cube
de quel plan diable cherche-t-on dans cet exo a construire les intersections avec les faces du cube ???
c'est quoi l'énoncé, tu peux le relire ?
pourquoi ton énoncé est faux (mal recopié, ne correspond pas aux figures pour les noms des points et la définition de ces points) ?
même principe que pour l'exo 1
si oui pourquoi ?
qu'est ce qu'on cherche à faire en traçant ça ?
(réponse précise, rédigée comme en Terminale, et pas "à faire l'exo" )
on obtient un nouveau point de la section appeler N où ça précisément ?
le dire et le justifier
ou au moins le placer effectivement sur la figure si tu refuses de rédiger ton raisonnement et que tu le gardes pour toi. (ton correcteur appréciera ..)
Non je refuses pas j'essaye juste de voir comment on a fait pour la première figure et le référe pour la deuxième. Donc voilà ma figure :

Oui c'est bien ça (rédiger, c'est vraiment pas ton fort, ça va te donner des points en moins l'absence de rédaction correcte)
ensuite ce point N qui par construction (droite (MK)) est dans (CDHG) (et (JKL)) se trouve effectivement aussi dans (EADH)
que peut on faire de ça ?
qu'est-ce qu'on cherche (ne pas perdre de vue l'objectif des intersections du plan (JKL))
bon OK, ça sert à tracer [NL], d'accord (paru entre temps)
comment continuer ?
c'est là que le théorème sur les plans parallèles peut être utile...
Je trace la parallèle à (LJ) en partant du point K car (EHGF) et ((ABCD) sont deux plans parallèle. J obtiendrais un nouveau point sur la droite CB
tout à fait.
vient maintenant la question à 2€
Quel polygone obtient-on ?
le décrire précisément et exactement (ne pas rester dans le vague)
pour cela ....
... une remarque : les parallèles vont de pair avec le théorème de Thalès qui n'est pas là loin ...

et puis autre chose aussi d'ailleurs
un peu plus compliqué certes : utiliser les symétrie du cube par exemple,
au pire calculer avec Pythagore, ou tout au moins "faire comme si on calculait" pour prouver que certains segments sont égaux.
Comme on a utiliser la propriété des plan parallèle alors, JP//NK et LJ//KO et LN//PO
Ainsi on obtient un hexagone. Il est nécessaire de continuer à justifier ?
"un hexagone" oui, et pour ça il suffit de compter les côtés :
n'importe quel polygone à 6 côtés s'appelle un hexagone.
d'accord, en plus celui-ci a une particularité : ses côtés opposés sont parallèles deux à deux.
mais celui là aussi :

donc il faut poursuivre (pour prouver pourquoi notre hexagone est en ffait régulier)
c'est quand même grave en terminale de ne pas savoir inclure une image correcte ... quand on est né dans le numérique ...

les images, on ne sait faire que des selfies à l'ère du numérique
donc le téléphone pour prendre des photos, et le système d'orientation automatique des images fait comme le système de frappe automatique et comme celui de dictée automatique : il n'en fait qu'à sa tête...
ceci n'empêche pas de savoir utiliser la convention des arêtes cachées pour indiquer quelle droite/segment se trouve sur une face cachée du cube et quelle droite/segment est sur une face visible ...
et ça, ça n'a rien à voir avec le numérique...
comme le fait de savoir rédiger ses raisonnements et démonstrations...
j'ai arrêté de relever ces manquements à chaque message ou presque : c'est à mon avis sans espoir.
bien sur ...
juste une remarque : quand je pense qu'on doit leur "valider" le BII (brevet informatique et ...) ou du moins un certain nombre d'items ...