Inscription / Connexion Nouveau Sujet
Continuité / Continuité uniforme 
Bonjour à tous 
Alors voilà, on fait un peu de logique en cours là et on veut montrer l'importance de la place des quatificateur dans une relation :
Pour moi ce qui change entre les deux relations c'est que dans le
Enfin on se choisis un nombre
Alors que dans la première relation le
Voilà voilà, je ne sais pas trop si je m'exprime clairement d'autant plus que la différence entre les deux relations est tout de même subtile pour quelqu'un qui ne s'y est jamais frotté ^^
Merci d'avance !

bonsoir
tu as en partie raison... mais dans aucun cas le "alpha" ne dépend du "x'" car ce dernier est toujours placé après le choix du alpha...
Bonsoir Alain 
Tout d'abord, merci de ta réponse très rapide ! 
En disant que le alpha dépend du x je voulais exprimer la même chose que ce qui tu as ecris dans ton second poste :
(*) : alpha dépend du x où on travaille

Donc enfait on veut montrer dans le cas de la convergence uniforme que la fonction est bornée sur le I considérée où je fais fausse route ?
Merci d'avance

Salut !
La continuité veut dire en gros que pour n'importe quel x, on peut être aussi proche de f(x) pourvu qu'on soit proche de x.
L'uniforme continuité veut dire que pourvu que x et x' soient dans un intervalle suffisamment petit, leurs images sont aussi proche que l'on veut.
Vois-tu alors la nuance?
Euh oui tout à fait
Donc dans le petit exercice qu'on nous à donné pour mieux comprendre :
On considère l'application de dans
qui à
associe
Je vois bien que la bête n'est pas continue uniformément mais je n'arrive pas à le montrer ..
De même à mon avis la fonction arctangente est uniformément continue mais la c'est surement plus simple à prouver ..

Salut Nightmare 
Euh pour tout te dire je n'arriverais pas à dire ce qui diffère d'une proposition à l'autre bien que je vois qu'elle ne sont pas équivalente .
Merci de vos réponses 
Mon problème : Je n'arrive pas à montrer que la fonction carré de IR dans IR n'est pas uniformément continue
On voit bien que la fonction carré n'est pas uniformément continue sur x² du fait de sa croissance rapide. On aura beau être dans un petit intervalle, on va toujours pouvoir trouver de grands écarts entre les images.
En l'occurrence, prenons par exemple un écart de 1 entre les images. Si on avait continuité uniforme cela voudrait dire qu'on va pouvoir trouver un (longueur des petits intervalles) tel que dès que x et x' sont à distance inférieure à
leur image serait à distance inférieur à 1. Ce résultat est faux, il suffit de prendre le premier égal à
et le deuxième par exemple à
ces deux nombres sont à distance inférieure à et pourtant la distance entre leurs images est supérieure à 1 !
supposons qu'il existe  >0 tel que
>0 tel que
 x, x'
x, x' 
 ;|x-x'|
;|x-x'|

 |x²-x'²|
|x²-x'²| 1
1
(je prends avec  =1)
=1)
et essaye d'arriver à une contradiction
En fait, sur un segment - plus généralement un compact - les deux définitions sont équivalentes (c'est le théorème de Heine).
La différence entre la continuité et la continuité uniforme c'est la notion d'uniformité. La continuité ça dit qu'en gros le graphe ne présente pas de coupure. La continuité uniforme ça dit que non seulement il ne présente pas de coupure mais en plus il a un comportement uniforme, c'est à dire qu'on n'a pas de trop fortes variations (grossièrement)
Je t'invite à montrer le résultat très pratique suivant : Si f est uniformément continue, alors il existe a et b tels que pour tout x, .
Ce résultat est pratique dans sa contrapposée : Si f ne se majore pas par une fonction affine, elle ne peut être uniformément continue (c'est le cas de la fonction carré par exemple)
Ah oui ça à l'air très efficace comme résultat 
Je vais essayer de faire ça en supposant f uniformément continue, je vais bien voir ce que ça donne ^^
En tout cas j'apprécie beaucoup vos explications à vous deux, je vous en remercie infiniment 
Bonsoir tout les trois,
et pour en rajouter une couche sur le résultat qu'énonce Nightmare(dont je salue le retour au passage), celà montre en particulier que les fonctions polynômes de degré supérieur ou égale à 2 ne sont pas uniformément continue sur [0,+oo[...

Salut robby 
Oui, et comme on s'en doute, c'est beaucoup plus simple de le montrer ainsi que de revenir à la définition 
Salut robby 
Ah oui, je le retiendrais ça aussi 
Pour le résultat à démontré (proposé par Nightmare), je pense avoir fait quelque chose qui pourrait aider, on doit bien utiliser l'inégalité triangulaire ?
J'arriverais à me contenter d'un oui ou d'un non ^^ (En cas de oui je poste ce que j'ai fais)

Oui on va bien utilisé l'inégalité triangulaire mais il faut voir comme on va découper notre intervalle ! L'idée (comme souvent) est de faire un dessin 
 Je vois absoluement pas quel dessin faire mais je vais chercher un peu, j'ai tendance à vouloir trop vite la réponse sans chercher en profondeur et faudrait que que j'arrive à changer ça..
Je vois absoluement pas quel dessin faire mais je vais chercher un peu, j'ai tendance à vouloir trop vite la réponse sans chercher en profondeur et faudrait que que j'arrive à changer ça..
Donc je reviendrais vous voir quand j'aurais trouvé quelque chose de complet où si j'ai vraiment trop de difficultés.
Merci beaucoup 
Merci pour le dessin, je n'ai pas encore eu vraiment le temps de regarder avec les devoirs que j'ai mais je vais regarder ça se soir 
Parcontre un truc qui va surement m'aider, la réciproque n'est pas forcément vrai non ?
Merci d'avance 
non,la réciproque n'est pas forcément vraie et d'ailleurs il me semble que qu'il faut que f soit définie dans [0,+oo[...ou en tout cas,pas dans R tout entier car la fonction valeur absolue est 1-lipschitzienne,donc unif-cont,mais elle n'est majorée par aucune fonction affine sur R...enfin,je crois...à confirmer.
sinon,trés bien ce dessin!

Bonsoir,
Non la reciproque ne marche pas, par exemple la fonction sin(1/x) sur ]0,+oo[, on peut la borner par une fonction affine mais elle n'est pas unif continue.
Salut Rodrigo 
Merci pour vos réponses, ça m'aide tout de même un peu de savoir que la réciproque ne marche pas 
Ben je vais essayer de continuer dans cette voie alors 
Bon.. je baisse les bras.
Je fais des calculs bizard avec les valeurs absolues qui je ne suis même pas sur de bien savoir manipuler et au final je n'ai rien qu'y convient.
Graphiquement j'ai l'impression qu'il faut que la hauteur des rectangles devrait rester plus ou moins stable et qu'elle ne doit pas devenir de plus en plus grande mais bon j'en suis pas sur et ça m'aide toujours pas pour les calculs en fin de compte.
Donc voilà, si quelqu'un voulait bien m'aider 
écrit la définition de la continuité uniforme avec epsilon=1 et considère un entier n non nul tel que x/n soit inférieur ou égale à eta (cet entier n exsite bien,par exemple n=E(x/eta)+1 convient)
puis considère ta définition pour k dans [0,n-1]...je te laisse poursuivre...
(sauf erreurs d'indications)
Merci  Mais je suis toujours les deux pieds dans le noir.. Je continuerais demain car la j'ai de l'anglais et un détecteur de crête& equa. diff. party pour demain
Mais je suis toujours les deux pieds dans le noir.. Je continuerais demain car la j'ai de l'anglais et un détecteur de crête& equa. diff. party pour demain
Bonne soirée, merci encore pour l'aide que vous m'apportez
A demain 
je te fais le début plus "explicitement..."
Soit
Soit
Soit , et
tq
ainsi
on a par uniforme continuité de
:
donc
et l'inégalité triangulaire nous dit que:
je te laisse poursuivre,sachant que j'ai pris ...
c'est quasiment fini...
sauf erreur
 Je pouvais chercher longtemps alors
Je pouvais chercher longtemps alors  J'aurais jamais pu trouver un truc pareil mais je vois plus ou moins où tu veux en venir
J'aurais jamais pu trouver un truc pareil mais je vois plus ou moins où tu veux en venir 
Je répondrais cette nuit avant de me coucher 
C'est super sympa d'avoir pris le temps de détailler tout ça et en en plus !


 plutôt que des
plutôt que des 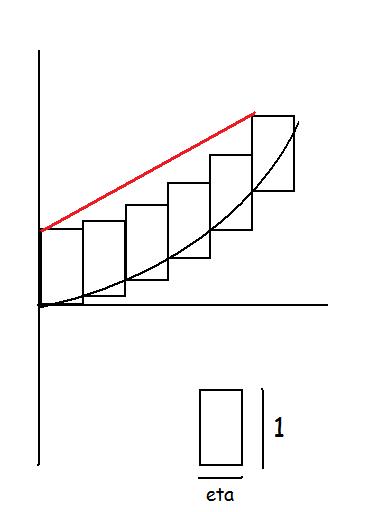

 analyse en post-bac
analyse en post-bac